Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Витебский государственный университет им. П. М. Машерова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ДС Радиооптика_1 / Литература ч.1 / 72

.pdf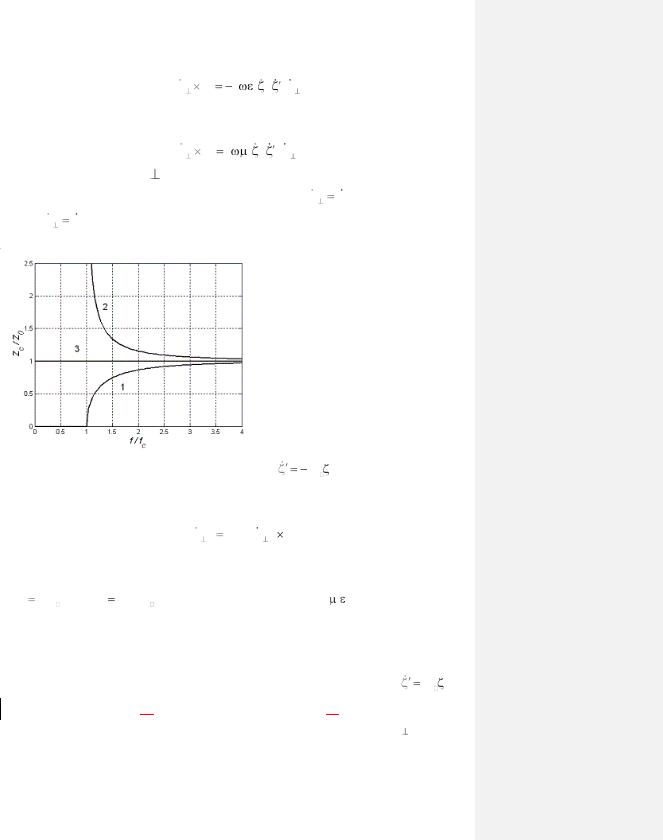

Скачиваний:

Добавлен:

14.04.2015

Размер:

1.34 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

He ez i ( / )Ee .

Для Н-волн найдем аналогичное соотношение, используя принцип перестановочной двойственности:

Em ez i ( / )Hm.

Здесь индексом " " обозначены поперечные составляющие

электромагнитного поля. Для волны E-типа He		He , а для волны H-
типа Em Em .
	Таким		образом,		в
	любой	точке		поперечного
	сечения	линии передачи
	поперечные		составляющие
	векторов		напряженности
	электрического и магнитного
	полей	перпендикулярны,			а
	отношение		их	длин	не
	зависит	от		поперечных
	координат.
	Для падающей волны
Рис. 3.7. Зависимость	i k	и		полученные
характеристического сопротивления ЛП	выражения			приобретают

следующий вид:
Ee,m Zce,m (He,m	ez ),			(3.49)

где Zce,m — характеристическое сопротивление ЛП для E- и H- волн, соответственно. Из полученных соотношений следует, что

Z e	Z	k / k; Z m		Z	k / k ,	(3.50),	где	Z = ( / ) –характеристическое
c	0		c	0				0
сопротивление среды, заполняющей ЛП.
	В		падающей волне поперечные					составляющие векторов

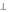составляют правую тройку с ортом оси z и с ортом направления распространения волны e= ez. В отраженной волне i k и указанные векторы образуют левую тройку. Однако, поскольку направление распространения отраженной волны e= –ez, E , Ни e по-прежнему образуют правую тройку векторов.

Из выражений (3.50) следует, что характеристическое

сопротивление	линии	передачи,	вообще	говоря,	комплексно
(Zc = Rc + iXc) и	зависит	от частоты,	причем	для E- и	H- волн эта

зависимость различна. Для Т-волны k|| = k и ее характеристическое сопротивление от частоты не зависит. На рис. 3.7 показана частотная

зависимость	характеристических сопротивлений	Zce	(кривая	1),	Zcm
(кривая 2) и Zct (кривая 3) для k = const и			= 0. При	k > k
характеристическое сопротивление действительно			(Zc = Rc),	т.	е.
поперечные	составляющие электрического и	магнитного		полей

находятся в фазе. На частотах ниже критической (k < k ) характеристическое сопротивление реактивно (Zc = iXc), т. е. указанные составляющие сдвинуты по фазе на 90°, причем для E-волн Xc > 0 (индуктивное сопротивление), а для H-волн Xc < 0 (емкостное сопротивление). Характеристическое сопротивление ЛП с потерями комплексно на всех частотах.

Запишем выражения для электромагнитного поля Е-волн (3.45) – (3.46) в проекциях на оси обобщенно-цилиндрической системы

координат x1, x2, z. Учитывая,

что

для падающей волны

i k ,

найдем

i k

i k z ;

i k

E2e

i k z ;

(3.51)

k 2 e e i k z ;

i k

H e

e i k z ;

Z0 g2

i k

H2e

e i k z ;

(3.52)

H e

Z0 g1

Для поля Н-волн получим аналогичные выражения с помощью принципа перестановочной двойственности:

Отформатировано: По правому краю

i kZ0

i k z

;

i kZ0

e i k z ;

(3.53)

	i k	m
H e			e

1	g1	x1

	i k	m
H e			e

2	g2	x2

i k z

;

(3.54)

H e	k 2 m e i k z ;
z

Полученные формулы позволяют анализировать зависимости различных составляющих электромагнитного поля от координат, а также построить картины силовых линий (эпюры) векторов E и H, позволяющие наглядно представить распределение поля в ЛП. Силовой линией (линией тока) векторного поля называют кривую, касательная к которой в каждой точке совпадает с направлением вектора поля в этой точке. Из этого определения следует, что силовые линии в ортогональной системе координат удовлетворяют дифференциальным уравнениям

Отформатировано: По ширине,

Отступ: Первая строка: 1,27 см

g1dx1	g2dx2	g3dx3	.	(3.55)
			.	(3.55)
A1	A2	A3

Более подробные сведения об уравнениях силовых линий содержатся в Отформатировано: По ширине приложении 8.

Уравнения (3.55), как правило, приходится решать численно3. Однако, приближенную картину силовых линий в поперечном сечении волновода можно построить и без решения этих уравнений. Это построение целесообразно начинать с изображения поля, которое для данного типа волны не имеет продольной составляющей, так как его силовые линии лежат в плоскости поперечного сечения волновода. Так, для Е-волн уравнение силовых линий магнитного поля имеет вид (П5.2): e = C1, т. е. силовые линии поля H в данном случае — это линии уровня мембранной функции.

3 Именно таким способом рассчитаны и построены все приведенные в книге эпюры силовых линий.

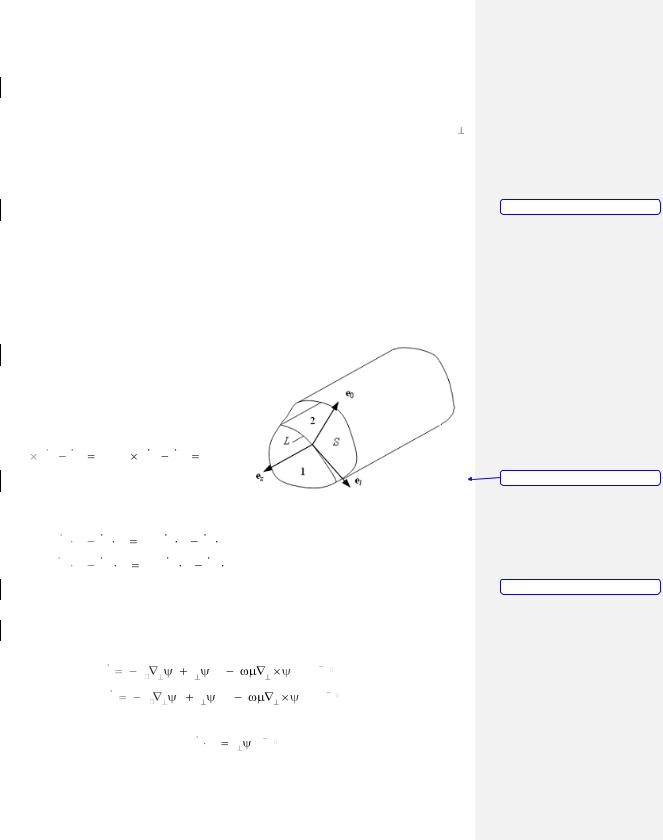
Построив силовые линии вектора Н, легко изобразить проекции силовых линий вектора E на плоскость поперечного сечения волновода, воспользовавшись ортогональностью векторов E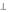 и Н . Аналогично строятся эпюры силовых линий и для H- волн.

3.6. Граничные условия для мембранной функции

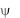Определим граничные условия, которым должна удовлетворять мембранная функция на поверхности раздела сред, образующих линию передачи. Поскольку в качестве таких сред используются диэлектрики и металлы, рассмотрим поверхности раздела между двумя диэлектриками и между диэлектриком и металлом, считая его идеально проводящим. Полагаем также, что поверхностные токи и заряды отсутствуют.

На поверхности раздела двух диэлектриков S (рис. 3.8) касательные составляющие полей должны быть непрерывны (см. раздел 1.4):

Отформатировано: По ширине

e0 (E2

E1 ) 0; e0

(H2 H1) 0.

Каждое

из

этих

векторных

Отформатировано: По ширине

равенств

сводится

двум

скалярным:

E1 ez

Рис. 3.8. К выводу граничных условий

(3.56)

для мембранной функции

(3.57)

где el — орт касательной к поверхности раздела, лежащий в плоскости Отформатировано: По ширине поперечного сечения ЛП.

В общем случае электромагнитное поле падающей волны в ЛП представляет собой суперпозицию E- и H-волн:

E	(	ik	e	k2	ee	z	i	me	z	) e i k z ;	(3.58)
						z			z
H	(	ik	m	k2	mez		i	eez ) e i k z .			(3.59)

Найдем проекции этих векторов на указанные направления:

E e

k 2 e e i k z ;

E e

[ i k (

e e

k 2

(

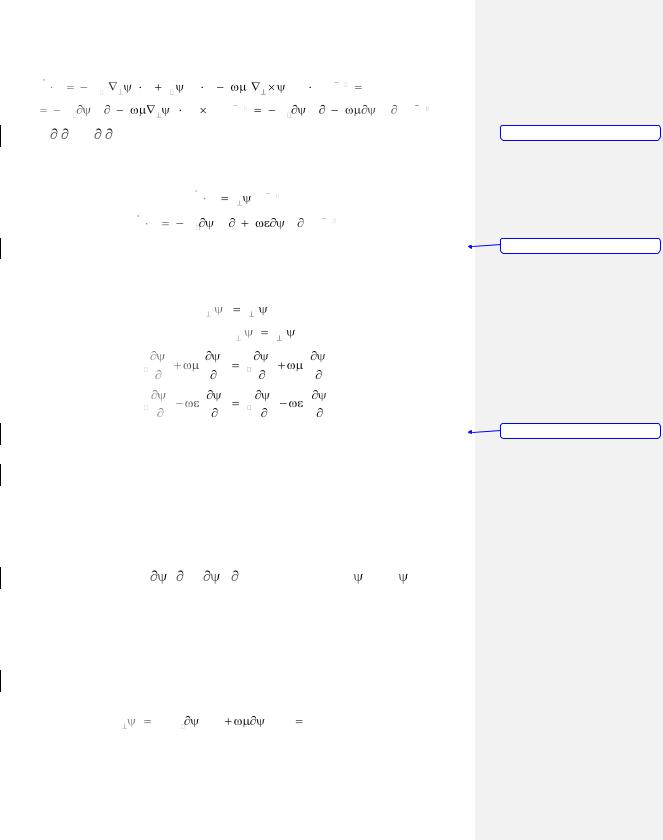
) e

]e i k z

[ i k

e / l i

)]e

i k z

( i k

e / l i

m / n) e i k z .

Здесь / n и / l — производные по нормали и касательной к контуру поперечного сечения поверхности раздела L. (см. рис. 3.8). Аналогичные формулы справедливы и для проекций вектора H:

Отформатировано: По ширине

H e

k 2 m e i k z ;

H e ( i k m / l i	e / n) e i k z .
l

Подставив полученные выражения

равенства

(3.56), (3.57),

Отформатировано: По ширине

получим

k 2

m ;

(3.60)

k 2

;

(3.61)

;

(3.62)

(3.63)

В этих выражениях индексами 1 и

обозначены

величины,

Отформатировано: По ширине

относящиеся к первой и второй средам, соответственно.

Анализ полученных граничных условий показывает, что в общем

случае E- и H-волны в линии передачи не разделяются. Такие волны

называют смешанными или гибридными, обозначая их символами EH

или HE в зависимости преобладания

продольной

составляющей

электрического или магнитного поля.

Однако, если

l =

l = 0. (функции e

m имеют

постоянные значения на контуре поверхности раздела), граничные

условия (3.62) и (3.63) разделяются. Это означает, что в данном случае

E- и H-волны могут существовать в ЛП независимо друг от друга и

уравнения (3.25) можно решать для каждого типа волн отдельно.

На

поверхности

идеального

проводника

касательная

составляющая электрического поля обращается в нуль

k 2 e

0; k

e / dl

m / dn

(3.64)

Индексы, обозначающие среду, здесь опущены, так как во второй среде (металле) поле отсутствует.

Из первого равенства следует, что при k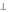 0 функция e должна обращаться в нуль на контуре L металлической поверхности ЛП. Таким образом для E-волн в металлических ЛП должно выполняться граничное условие

	e = 0 на L.	(3.65)
Очевидно, что и	e/ l = 0 на L. Тогда из второго равенства (3.64)
получаем граничное условие для H-волн
	m/ n = 0 на L.	(3.66)
Волны типа T можно рассматривать как частные случай E-волн
при k = 0. В	этом случае первое условие (3.64)	выполняется
тождественно, а из второго условия следует(функция		m для E-волн
тождественно равна нулю):
	e/ l = 0 или e = const на L.	(3.67)

Таким образом, мембранная функция T-волны должна иметь постоянное значение на контуре металлической поверхности.

Из граничных условий (3.65) – (3.67) следует, что в металлических линиях передачи Е-, Н- и Т-волны могут существовать независимо друг от друга (если считать металл идеально проводящим).

Отметим, что для волн Т-типа мембранное уравнение (3.25) сводится к уравнению Лапласа, и его решение принадлежит к классу гармонических функций. Теорема о гармонических функциях утверждает, что если эта функция принимает постоянное значение на границе расчетной области S, (а это следует из граничного условия), то она постоянна и всюду в области S. Согласно (3.45), (3.46) электромагнитное поле, описываемое такой функцией, тождественно равно нулю, т. е. существование Т-волн в данном случае невозможно. В многосвязных линиях передачи на каждой из направляющих


цилиндрических поверхностей функция			может принимать
постоянные значения	1,	2,..., отличные друг от друга. В этом случае
мембранная функция	не	постоянна в поперечном сечении ЛП и

Отформатировано: По ширине

определяет не нулевое электромагнитное поле. Отсюда следует, что T- волны могут существовать только в многосвязных линиях передачи.

3.73. Спектр типов волн в линии передачи и их ортогональность
	Распределение электромагнитного поля свободных волн		в	Отформатировано: По ширине
поперечном сечении линии		передачи описывается функцией	,
удовлетворяющей однородному уравнению Гельмгольца (3.25).
Предположим, что эта функция известна. Тогда, помножив уравнение
(3.25) на * и проинтегрировав полученное равенство по поперечному
сечению ЛП, получим
*		dS k 2 \| \| dS 0.
	S	S

Преобразуем первый интеграл с помощью двумерного аналога теоремы Грина (П1.26):

Отформатировано: По ширине

	*
		dl	\|	\|2 dS k 2 \| \|2 dS 0.

L	n		S	S

Отсюда

						*
		\|	\|2 dS				dl
	2	\|	\|2 dS			n	dl
k	2	S			L	n		.	(3.68)

			\|	\|2	dS.
			\|	\|2	dS.

В ЛП с идеально проводящими стенками на контуре поперечного сечения L либо = 0, либо / n = 0, поэтому первый интеграл обращается в нуль. Следовательно, в данном случае имеет место так называемое частное Рэлея.

Отформатировано: По ширине

		k 2	\|		\|2 dS		(3.69)
			S			.
				\|2		.
			\|	\|2	dS
			S
Как видно, k	2	0, т. е.	все		критические		волновые числа	Отформатировано: По ширине
Как видно, k		0, т. е.	все		критические		волновые числа

действительны. Однако, если стенки волновода не идеально проводящие, на них выполняются граничные условия Леонтовича (5.14). Контурный интеграл в этом случае имеет отличное от нуля комплексное значение, следовательно, и критические волновые числа комплексны.

В вариационном исчислении показывается, что выражение (3.69)

является функционалом, стационарным на решении задачи (3.25) с

граничными условиями Дирихле или Неймана. Это означает, что

небольшие изменения функции

приводят к изменению k 2 второго

порядка малости. Поэтому формулу (3.69) можно использовать для

приближенного определения критического волнового числа по неточно

найденной мембранной функции.

Запишем уравнение (3.25) в более общем виде:

(3.70)

где

= –

—

дифференциальный

оператор,

= k

. Решениями

Отформатировано: По ширине

этого уравнения являются функции, результат воздействия на которые

оператора

сводится к

их

умножению на

некоторое

число .

Нетривиальные решения уравнения (3.70) существуют только при

определенных значениях

параметра

называемых

собственными

значениями

оператора

Каждому

собственному

значению

соответствуют одно или несколько решений, называемых

собственными функциями оператора. В последнем случае собственное

значение считается вырожденным, причем кратность вырождения

равна числу линейно независимых собственных функций,

принадлежащих этому значению. Совокупность всех собственных

значений оператора называется его спектром. Из функционального

анализа известно, что спектр оператора

с однородными граничными

условиями Дирихле (3.65) или Неймана (3.66) дискретный и содержит

бесконечное счетное множество положительных собственных

значений. Это означает, что их можно пронумеровать в порядке

возрастания: 0 <

3 …

В граничные условия (3.62), (3.63) входит волновое число,

поэтому собственные значения и функции оператора

для гибридных

волн

могут

зависеть

от

частоты как

от параметра. Кроме того,

собственные значения могут быть комплексными. Следовательно, гибридные волны могут иметь, наряду с дискретными собственными значениями, участки непрерывного спектра. В дальнейшем в этой главе рассматриваются ЛП с дискретным спектром.

Методами вариационного исчисления доказывается, что в любой односвязной ЛП с однородным изотропным заполнением основной является волна типа H. Качественно эту теорему можно подтвердить тем, что граничные условия Неймана (H-волны) более "мягкие", чем условия Дирихле (E-волны) и позволяют мембранной функции медленнее изменяться в поперечном сечении ЛП (в частности, эта функция может быть постоянна вдоль некоторого направления).

Поэтому интеграл по площади поперечного сечения	от \| \|2	для
основного типа H-волн не больше, чем аналогичный	интеграл	для

основного типа E-волн, в то время как для интегралов от | |2 наблюдается обратное соотношение. Так как значения поперечных волновых чисел определяются частным Рэлея (3.69), отсюда следует справедливость сформулированной выше теоремы.

Собственная функция 1, соответствующая наименьшему собственному значению 1 оператора , определяет основной тип волны в данной линии передачи. Он обладает наибольшей критической

длиной волны	c1 = 2 n/	1/2	(наименьшей критической частотой fc1).
		1

Все остальные собственные функции 2, 3, … определяют высшие типы волн, имеющие критические частоты fс2, fс3, ..., не меньшие, чем критическая частота основного типа волны.

Очевидно, что на частотах f < fс1 распространение волн в линии передачи невозможно. В интервале частот fс1 < f < fc2 в линии может распространяться только один, основной тип волны (одномодовый режим работы ЛП) Этот интервал называют рабочим диапазоном частот линии передачи. На практике ширину рабочего диапазона выбирают несколько меньше теоретической — от 1.25fc1 до 0.95 fc2, так как вблизи критической частоты fс1 увеличивается затухание основного

типа волны, а вблизи fс2		возникает опасность возбуждения высших
типов волн.
Число типов волн N, критические частоты которых лежат в
интервале	, определяется асимптотической формулой Куранта, тем
более точной, чем больше		:
		N = S/( c2)	,

100

где S—площадь поперечного сечения линии передачи. Отношение
N = N /	= S	//( c2)	(3.71)
называют плотностью спектра собственных волн. Как следует из
формулы Куранта, плотность спектра собственных волн в ЛП растет
пропорционально первой степени частоты.
Так как оператор Лапласа с граничными условиями (3.65) или				Отформатировано: По ширине
(3.66) является самосопряженным (см. приложение 2), его собственные
функции ортогональны:
m	n dS	0, m	n.
S

Из этого равенства следует ортогональность электромагнитных полей различных типов свободных волн в линиях передачи Для доказательства рассмотрим, например, Е-волны. Вычислим интеграл

Отформатировано: По ширине

(

n )dS.

E mE n dS

m n

Воспользовавшись теоремой Грина (П1.26), получим

*k 2

dS 0.

E m

Такое же равенство справедливо и

для

магнитного поля.

Отформатировано: По ширине

Действительно, вычислим

2 2 (

) (

)dS.

Согласно векторному тождеству (П1.15),

mez [

(

nez )]dS

[(

mez )

nez ]dl .

Преобразуем первое подынтегральное выражение:

[

(

)]dS

[ (

)

k 2

m n

(первое слагаемое в квадратных скобках равно нулю, так как функция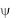не зависит от координаты z). Интеграл по контуру поперечного сечения ЛП равен нулю вследствие граничных условий. Раскрыв двойное векторное произведение, найдем

Отформатировано: По ширине

101

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Соседние файлы в папке Литература ч.1

#
14.04.20155.17 Mб392177_____.doc
#
14.04.20151.34 Mб5672.pdf
#
14.04.20151.22 Mб55[Kostyurina_A.G.,_Kushnirenko_E.A.,_Lebedev_V.A.,_(BookFi.org).pdf
#
14.04.20153.18 Mб263Введение в радиооптику.pdf
#
14.04.20156.53 Mб166История техники связи.pdf
#
14.04.2015204.34 Кб44односвязные злп.pptx
#
14.04.20151.77 Mб117Оптические системы передачи (Дмитриев А.Л., 2007).pdf