ДС Радиооптика_1 / Литература ч.1 / 72

имеет продольной составляющей вектора H, а в поле H-типа отсутствует продольная составляющая вектора E1. В общем случае электромагнитное поле в ЛП представляется суперпозицией Е- и Н- полей (волн). Уравнение (3.17) в разделяющейся системе координат имеет вид

Отметим, что, в отличие от (3.17) это двухмерное уравнение.

Таким образом, в разделяющихся системах координат краевая задача о свободных волнах сводится к решению двух уравнений типа (3.18) для проекций электрического и магнитного векторов Герца на ось x3. Отметим, что в этих уравнениях неизвестные функции разделены и их связь возможна только через граничные условия. Наличие или отсутствие этой связи определяется формой граничной поверхности. Если указанная связь отсутствует, уравнения (3.18) или (3.19) для электрического и магнитного векторов Герца можно решать по отдельности, что значительно упрощает их решение.

Используем для решения уравнения (3.18) метод разделения переменных Фурье. Для этого представим проекцию вектора Герца в виде произведения двух функций, одна из которых зависит только от поперечных координат х1, х2, а другая — только от продольной координаты x3:

Нетрудно показать, что такое представление возможно, если уравнение граничных поверхностей имеют вид

1 В зарубежной литературе используются обозначения TM (Transverse magnetic) для поля E-типа и

TE (Transverse Electric) для поля H-типа.

82

Для доказательства этого утверждения предположим, что граничная поверхность определяется уравнением более общего вида f(x1, x3) = 0,

Первое слагаемое левой части зависит только от поперечных координат, а второе — только от продольной координаты x3. Правая часть (3.23) от координат не зависит. Очевидно, что равенство левой и правой части при любых значениях координат может выполняться, только если каждое из слагаемых не зависит от координат, т. е. если

83

"поперечный" оператор Лапласа, k 2 и k||2 — не зависящие от координат константы, связанные с волновым числом соотношением (3.24), штрихи означают дифференцирование по z. Отметим, что всем перечисленным выше условиям удовлетворяют обобщенно цилиндрическая (M = 1) и обобщенно сферическая (M = r) системы координат.

Соотношение (3.24) называют характеристическим уравнением

ЛП, а входящие в него величины k и k|| — поперечным и продольным волновыми числами. параметр k|| называют также постоянной распространения, а k — критическим волновым числом. Функцию 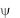называют мембранной функцией, поскольку она удовлетворяет уравнению мембраны (двумерному уравнению Гельмгольца) (3.25).

Общее решение дифференциального уравнения (3.26) в обобщенной цилиндрической системе координат (g3 = 1, M = 1) имеет

что позволяет написать следующее выражение для мгновенных значений вектора Герца:

z (x1, x2 , z,t) Am (x1, x2 ) cos( t k z A ) Bm (x1, x2 ) cos( t k z B ). (3.28)

Таким образом, электромагнитное поле в ЛП есть суперпозиция падающей и отраженной плоских неоднородных волн, имеющих одинаковое распределение электромагнитного поля в поперечном сечении линии и одинаковые (с точностью до знака) постоянные распространения k||. Поэтому в дальнейшем можно ограничиться рассмотрением падающей волны.

Из характеристического уравнения (3.24) следует, что если k и

84

Следовательно, в ЛП распространяется затухающая волна, скорость изменения амплитуды которой определяется мнимой частью, а фазы — действительной частью постоянной распространения. Поэтому величину называют постоянной затухания, а — постоянной фазы (фазовой постоянной) волны.

3.4. Дисперсия в линиях передачи

Выражение (3.30), определяющее поле падающей волны в продольно однородной ЛП аналогично по форме выражению (3.11), что позволяет воспользоваться для вычисления фазовой и групповой

Учитывая, что с первыми дифференциалами можно обращаться как с дробями, найдем

Отсюда

где u = c/n — скорость света в среде, заполняющей линию передачи.

85

Как следует из этого выражения, если показатель преломления среды и поперечное волновое число не зависят от k, фазовая и групповая скорости связаны соотношением vpvg = u2.

Из выражения (3.33) следует, что дисперсия в линии передачи наблюдается в тех случаях, когда скорость света в среде u = c/n (т. е. показатель преломления n) зависит от частоты и (или) волна неоднородна (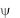 const и, согласно (3.25), k = 0). Неоднородность волны возникает при искажении ее поля телами, образующими линию передачи. Если, однако, функция 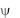принадлежит к классу гармонических, т. е. является решением уравнения Лапласа 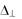= 0, k = 0 и дисперсия при n = const отсутствует.

Выражения (3.33) и (3.34) неудобны для анализа зависимостей фазаовой и групповой скорости от частоты, так как показатель преломления, входящий в волновое число в качестве сомножителя, сам может достаточно сложным образом зависеть от частоты (см. раздел 2.4.5). Чтобы упростить анализ, удобнее оперировать с замедлениями фазовой и групповой скоростей np и ng и волновым числом в свободном пространстве k0 = /c = 2 c/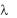 ( — длина волны в свободном пространстве). Очевидно, что

Соотношение (3.35) есть дисперсионное уравнение линии передачи.

Введем длину волны в линии передачи

g = /vp = 2 / ,

критическую длину волны

c = 2 n/k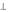

и критическую частоту

c = 2 c/ c = k c/n; fc = c/2 .

Используя эти выражения, можно преобразовать формулы (3.35) и (3.36):

86

Последнее выражение есть аналог формулы Рэлея (3.28) для волн в линии передачи. Из формулы (3.37) следует соотношение между длинами волн в ЛП и заполняющей ее среде:

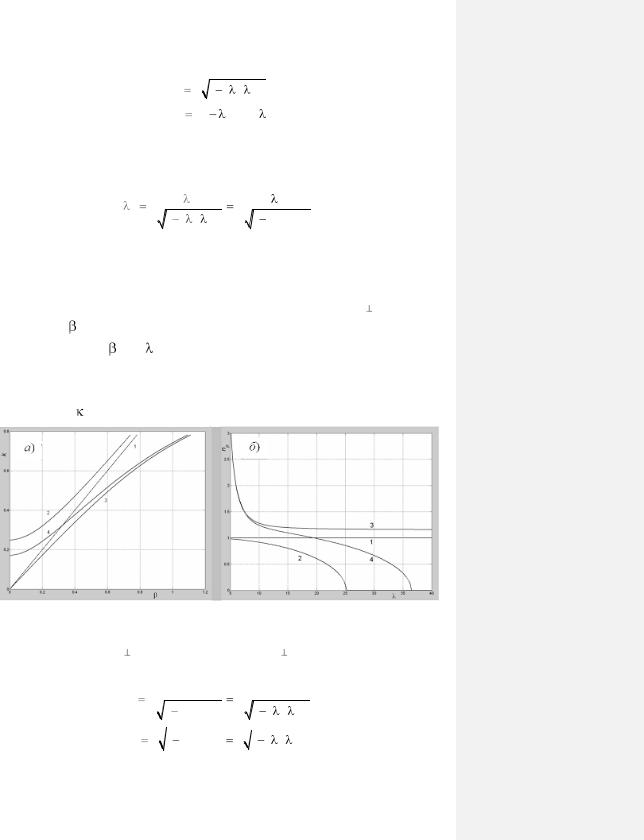
передачи, полагая коэффициент преломления среды n не зависящим от частоты, как это обычно имеет место в микроволновом диапазоне. Предположим сначала, что критическое волновое число k = 0. В этом случае k = n , np = n. Соответствующие дисперсионные характеристики

отсутствует, фазовая и групповая скорости равны скорости света, крутизна ДХ = 0.

Рис. 3.7. Дисперсионные характеристики линии передачи.

Пусть теперь k 2 = const > 0. Так как dk /dk0 = 0, из формул (3.37) и (3.38) следует:

87

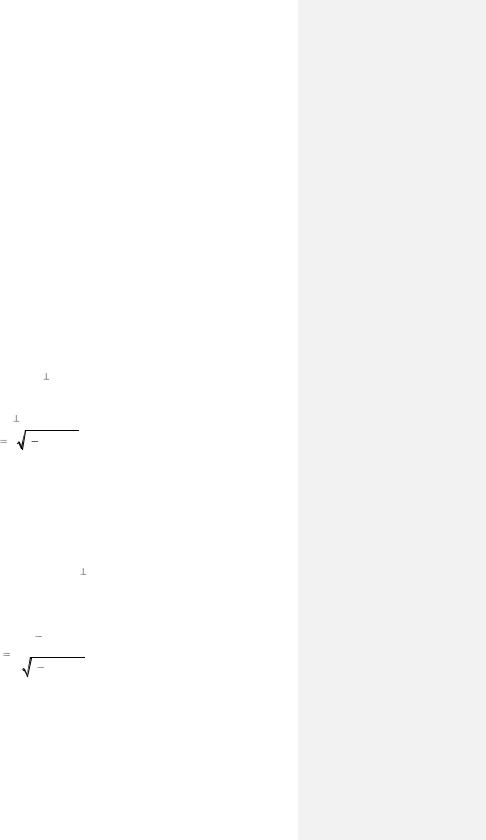
Соответствующие ДХ для n = 1 показаны на рис. 3.6 (кривые 2). Отметим, что в данном случае vpvg = u2. На малых длинах волн(в области высоких частот) фазовая и групповая скорости стремятся к скорости света в среде, заполняющей ЛП. При этом крутизна ДХ незначительна и уменьшается с ростом частоты. Когда длина волны, увеличиваясь, стремится к критической, фазовая скорость неограниченно возрастает, а групповая скорость стремится к нулю. Крутизна ДХ по мере увеличения длины волны увеличивается и вблизи ее критического значения стремится к бесконечности. В этих условиях понятие групповой скорости теряет физический смысл. Таким образом, распространение волн в ЛП возможно только на частотах, больших критической частоты (на длинах волн, меньших критической длины волны).

Рассмотрим, наконец, случай, когда критическое волновое число зависит от частоты. Положим k = ns(k0), где s — известная функция частоты (волнового числа в свободном пространстве). подставив в выражение (3.33) значение k , получим

Заметим, что если s — мнимое число, замедление фазовой скорости оказывается больше, чем показатель преломления среды. В линии передачи в этом случае распространяется медленная волна, так как ее фазовая скорость меньше скорости света в среде. Таким образом, доказана принципиальная возможность существования медленных волн в линии передачи. Неравенство k 2 < 0 следует рассматривать как необходимое условие существования этих волн.

Подставив выражение (3.42) в формулу (3.34), найдем:

Соответствующие дисперсионные характеристики обозначены на рис. 3.6 цифрой 3. Отметим, что медленная волна может иметь отличную от нуля частоту отсечки (кривые 4). Вблизи нее медленная волна превращается в быструю.

88

Замедление групповой скорости не может быть меньше, чем показатель преломления среды. Отсюда следует неравенство

Это неравенство накладывает ограничения на возможные зависимости поперечного волнового числа от частоты. Пусть, например, это число изменяется пропорционально частоте: s(k0) = ak0, где a —.коэффициент пропорциональности. Тогда неравенство (3.44) приобретает вид

np = ng = n(1 + 2).

Как видно, в этом случае групповая скорость равна фазовой, дисперсия отсутствует и замедления обеих скоростей больше, чем показатель преломления среды, т. е. в линии передачи распространяется бездисперсная медленная волна. Отметим, что пропорциональность критического волнового числа частоте может наблюдаться только в ограниченном диапазоне частот.

На частотах, меньших критической, постоянная распространения становится мнимой:

правой части, так как поле не может неограниченно возрастать с ростом координаты z). Амплитуда электромагнитного поля в ЛП экспоненциально убывает по мере увеличения координаты z, а его фаза не зависит от этой координаты. Такое поле не является волновым. В соответствии с выражением (3.39) групповая скорость имеет мнимое значение, т. е. распространения энергии вдоль ЛП не происходит. Описанный режим работы ЛП называют закритическим или

запредельным.

89

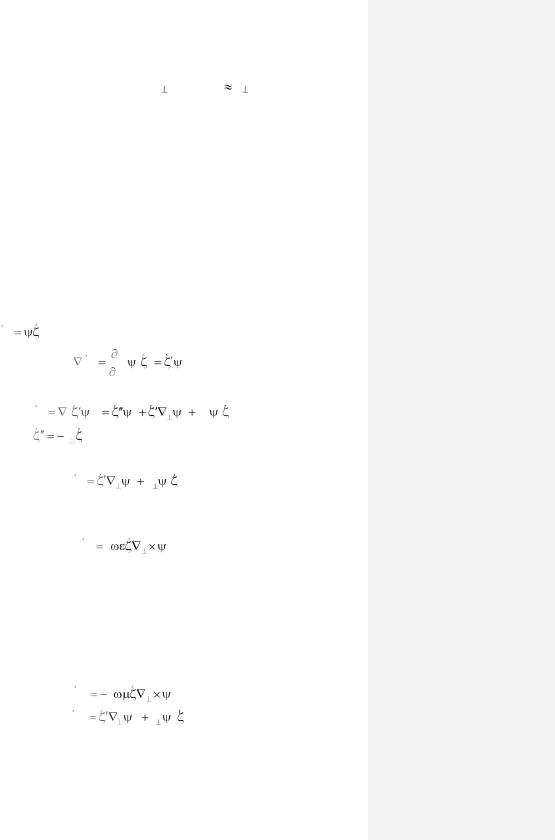
На достаточно низких частотах k/k <<1 и 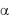k ., т. е. постоянная затухания не зависит от частоты. Эту особенность используют для создания микроволновых ослабителей (аттенюаторов), коэффициент ослабления которых слабо зависит от частоты.

3.5.Электромагнитное поле свободных волн в линии передачи

Впредыдущем разделе задача отыскания решений уравнений Максвелла в линии передачи была сведена к решению уравнения Гельмгольца для продольных составляющих электрического и магнитного векторов Герца. Если решения этих уравнений найдены, то электромагнитное поле, например, волн E-типа определяется с помощью соотношений (3.7), (3.8). Для того, чтобы воспользоваться

Подстановка выражения для вектора Герца в формулу (3.8) позволяет найти напряженность магнитного поля

При выводе этого выражения учитывалось, что ротор вектора направленного по оси z, содержит производные только по поперечным координатам. Поэтому функцию 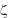можно вынести из под оператора Гамильтона.

Выражения для электромагнитного поля волны H-типа получим,

90

Из полученных соотношений следует, что при k = 0 электромагнитное поле волны в линии передачи имеет только поперечные составляющие. Такую волну называют поперечной, или T- волной2. Отметим, что отсутствие продольных составляющих поля волны наблюдается при тех же условиях, что и отсутствия дисперсии. Это обстоятельство отражает глубокую связь между строением электромагнитного поля волны и характером ее распространения в линии передачи.

Выражения (3.45) – (3.48) позволяют пояснить физический смысл мембранной функции . В случае Е- или Н-волн она пропорциональна продольной составляющей напряженности электрического или магнитного поля. Напряженность электрического поля Т-волны, как следует из (3.45), пропорциональна градиенту функции , удовлетворяющей двумерному уравнению Лапласа. Следовательно, для Т-волн мембранная функция играет роль скалярного потенциала электрического поля, определенного в плоскости поперечного сечения линии передачи.

Заметим, что продольные и поперечные составляющие электромагнитного поля бегущей волны в линии передачи без потерь ( i k ), как следует из (3.45) – (3.48), сдвинуты по фазе на 90°. Это означает, что электрическое поле Е-волн и магнитное поле Н-волн имеют эллиптическую, а магнитное поле Е-волн и электрическое поле Н-волн — линейную поляризацию.

В однородной плоской электромагнитной волне поперечные составляющие векторов Е и Н связаны между собой соотношениями (3.15). Найдем связь между этими величинами в линии передачи, для чего вычислим векторное произведение

Так как дивергенция постоянного вектора ez равна нулю, получаем

Сравнив полученное выражение с (3.45), найдем

2 В зарубежной литературе волны этого типа называют TEM (Transverse Electric and Magnetic)

91