ДС Радиооптика_1 / Литература ч.1 / Введение в радиооптику

Введение в радиооптику

волну единичной амплитуды, распространяющуюся из точки Р0 (так называемую функцию Грина свободного пространства [4, 8]). Таким образом, для функции G в произвольной точке Р1 имеем

G(P1) = exp(ikr)/r, (1.8)

где r − расстояние между точками Р и Р0.

При этом, как известно [8], функция G удовлетворяет неоднородному волновому уравнению

где δ(r) − дельта-функция.

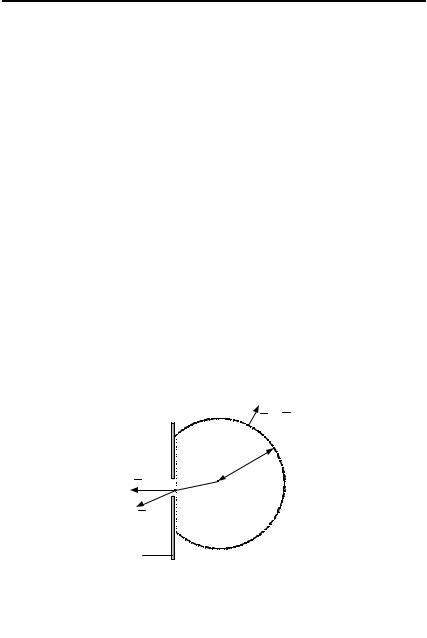
Согласно условиям теоремы Грина функция G, ее первая и вторая производные должны быть непрерывны в объеме V, ограниченном поверхностью S. Такое требование, как нетрудно видеть из (1.8), выполняется всюду, за исключением точки Р0, где функция G обращается в бесконечность. Поэтому для того, чтобы исключить точку разрыва, окружим P0 небольшой сферической поверхностью S0 радиусом r0. Применим теорему Грина для области V0, ограниченной поверхностью SΣ = S + +S0 (рис. 1.3).

Левая часть (1.7) формулы Грина с учетом того, что функции U и G удовлетворяют волновым уравнениям (1.6), (1.9), будет

∫(G 2 U − U 2G)dV = −∫(GUk2 − UGk2 )dV ≡ 0.

∫(G∂U / ∂n − U∂G / ∂n)dS = 0

SΣ

или

где cos(n, r0) − косинус угла между направлением внешней к единичной нормали n и единичным вектором r0, соединяющим точки P0 и Р1 (см. рис. 1.3); учтено также представление grad G в сферической системе координат.

Для случая, когда точка Р1 лежит на поверхности S0, n = − r0, cos(n,r0) = −l, и для (1.11), (1.12) имеем

Г.Г. Червяков, В.В. Роздобудько

Если R0 стремится к нулю, то в силу непрерывности функции U

Подставляя этот результат в (2.10), получаем

U(P0 ) = 0,25 / π∫(∂U / ∂n[exp(ikr) / r] − U∂ / ∂n[exp(ikr) / r]). (1.14)

S

Выражение (1.14) есть интегральное представление Кирхгофа (интеграл Кирхгофа), позволяющее выразить поле в произвольной точке Р0 через «граничные значения» поля на любой замкнутой поверхности, окружающей эту точку.

1.4 Дифракция на плоском экране с отверстием

Учитывая изложенное выше рассмотрим одну из встречающихся в радиооптике задач − дифракцию на отверстие в бесконечном идеально проводящем (непрозрачном) экране. Предполагается, что на экран с отверстием падает слева электромагнитная волна (ЭМВ). Она полностью отразится от экрана, за исключением отверстия Σ, через которое поле проникает в область за экраном, дифрагируя на ее краях. Таким образом, за экраном образуется дифрагированное поле, которое и необходимо определить в каждой точке Р0 этого бесконечного полупространства (рис. 1.4).

Рисунок 1.4 − К пояснению о дифракции на плоском экране

Формула Кирхгофа. Воспользуемся интегральным представлением Кирхгофа (1.14), выбрав соответствующим образом замкнутую поверхность S. Последняя состоит из двух частей (рис. 1.4): плоской по-

12

Введение в радиооптику

верхности S1, лежащей сразу за экраном и замыкающей ее полусферической поверхности S2 радиусом R → ∞ с центром в рассматриваемой точке

P0.

Функции U и G уменьшаются пропорционально 1/R, вследствие чего подынтегральное выражение в (1.14) будет в конечном итоге стремиться к нулю не медленнее 1/R2. Площадь интегрирования по S2 возрастает пропорционально R2, однако, если предположить существование сколь угодно малых потерь в среде, то при R → ∞ интегралом по поверхности S2 можно пренебречь.

Исследуя этот вопрос более детально, видим, что (1.13) на поверхности S2

где Ω − телесный угол с вершиной в точке P0, стягиваемый поверхностью

S2.

Величина |RG| равномерно ограничена на поверхности S2, поэтому полный интеграл по S2, будет стремиться к нулю при R → ∞, при условии, что

Это требование называется условием излучением Зоммерфельда. Легко убедиться, что условию излучения удовлетворяют решения (1.4), имеющие при R → ∞ вид расходящейся сферической волны

U(R) → U(θ, ϕ)exp(ikR)/R, где θ, ϕ − сферические координаты. Так как ЭМП, падающее на отверстие, можно представить в виде линейной комбинации сферических волн, то требование (1.17) будет удовлетворяться, и, следовательно, интеграл по S2 не будет давать вклада в общий интеграл. Заметим, что при замене exp(ikr) на exp(−ikr) в (1.8) определяем (учитывая временную зависимость в виде exp(−iωt)) так называемую сходящуюся сферическую волну (приходящую из бесконечности), лишенную физического содержания и как следствие не удовлетво-

ряющую условию (1.17) [4]. Итак, для рассматриваемой задачи

U(P0 ) = 0,25π−1 ∫(G∂U / ∂n − U∂G / ∂n)dS,

S2

где S, n показаны на рис. 1.4.

13

Г.Г. Червяков, В.В. Роздобудько

Далее при вычислении выражения для U(Р0) в рамках интегрального представления Кирхгофа принимаем, что:

−На отверстии Σ распределения поля и его производной ∂U/∂n имеют точно такие же значение, какие они имели бы в отсутствие экрана.

−На той части поверхности, которая лежит в области геометрической тени экрана, распределение поля U и ∂U/∂n тождественно равны нулю.

Таким образом, последнее выражение принимает вид

где интегрирование ведется только по поверхности отверстия Σ, а функция G определена выражением (1.8).

Хотя формула (1.18) существенно упрощает расчет поля в произвольной точке Р0 полупространства за экраном, однако в (1.18) содержатся физические несоответствия и математическая неточность.

Действительно, в соответствии с известными свойствами дифференциальных уравнений значения U во всех точках области однозначно определяются заданием на поверхности либо функции U (задача Дирихле), либо ее нормальной производной ∂U/∂n (задача Неймана), т.е. граничные значения U и ∂U/∂n, которые не могут выбираться произвольным образом, независимо друг от друга.

Полагая далее U и ∂U/∂n равными нулю на части плоской поверхности S1 (кроме отверстия), имеем в соответствии с теоремой теории потенциала, что они должны быть равными нулю на всей замкнутой поверхности (S1 + S2), т.е. и на отверстии, а это противоречит физической реальности.

Наконец, условие, что U и ∂U/∂n на отверстии Σ совпадают со значениями в этом же месте невозмущенной волны, можно принять лишь в случае, если D/λ >> 1 (D − линейные размеры препятствия, λ − длина волны). Об этом условии как основной предпосылке приближенной теории дифракции уже упоминалось выше [4, 8].

Формула Кирхгофа-Зоммерфельда. Одно из противоречий тео-

рии Кирхгофа было устранено Зоммерфельдом (который исключил необходимость одновременного наложения граничных условий на поле U и его нормальную производную) за счет введения специальной функции

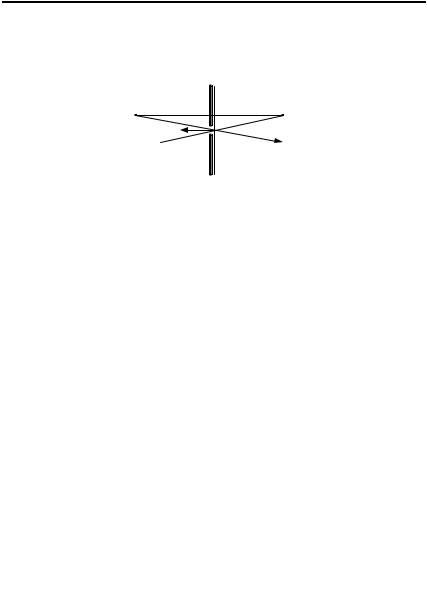
Р0 (рис. 1.5), и Р1.

14

Введение в радиооптику

Физически (1.19) означает, что функция G(P1) создается не только точечным источником, помещенным в точку Р0, но также и вторым

~

точечным источником, расположенным в точке P , которая представляет собой зеркальное отображение точки Р0 и лежит по другую сторону экрана.

Рисунок 1.5 − Схема для вывода формулы Кирхгофа−Зоммерфельда.

Соответственно

∂G/ ∂n =cos(n,r0 )exp(ikr)(ik −1/ r)/ r −cos(n,~r0 )exp(ik~r)(ik −1/ ~r)/ ~r.

Для точки Р1 на поверхности Sl имеем r =~r, cos(n,r0 ) =−cos(n,~r0 )

Выражение (1.21), полученное с учетом сделанных выше поправок, носит название формулы Кирхгофа-Зоммерфельда и является математической формулировкой принципа Гюйгенса-Френеля, согласно которому поле в любой точке наблюдения является результатом суперпозиции сферических волн exp(ikr)/r излучаемых элементарными источниками U(P1), распределенными на заданной поверхности Σ [4].

1.5 Дифракционная формула в приближениях Френеля и Фраунгофера

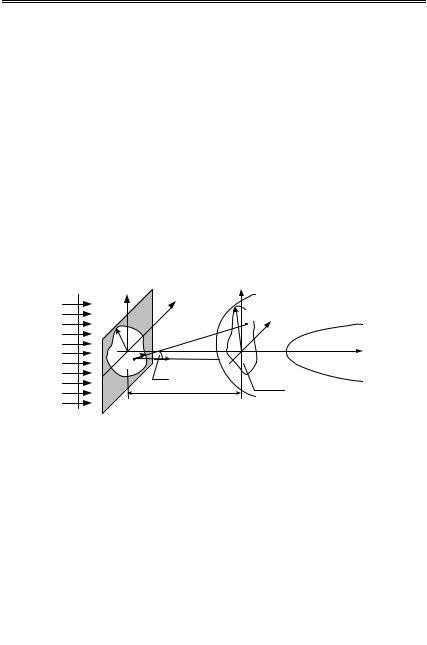
Полагая, что выполняются условия Кирхгофа, при которых было получено выражение (1.21) рассмотрим дифракцию монохроматической волны на экране с отверстием (рис. 1.6). Для удобства будем считать, что экран совмещен с системой координат (x0,y0,z0=0), а область наблюдения (x,y,z) с плоскостью, параллельной плоскости экрана x00z0 и расположенной на расстоянии z от нее (см.рис. 1.6 и 1.4). Тогда выражение (1.21) принимает вид

15

Г.Г. Червяков, В.В. Роздобудько

∞

U(x, y, z) =(iλ)−1 ∫U0 (x0 ,y0 , z0 )cosθzr exp(ikr) / r dx0dy0 , (1.22)

делы поставлены так как за пределами отверстия поле U0(x0,y0,0) равно нулю.

Приближение Френеля. Выражение (1.22) для дифракционного поля в области удаленной от экрана на расстояние, существенно превышающее максимальный размер апертуры Σ, значительно упрощается.

Так, если x – x0 ≤ z, y – y0 ≤ z, то полагая соsθzr ≈ 1 имеем ошибку менее 5 %, в случае если угол θzr < 18°. Эту область, вблизи оси 0z, представляющую наибольший интерес в радиооптикe называют параксиальной. Расстояние r в знаменателе подынтегрального выражения (1.22) заменяют на координату z (сделать такую же замену в экспоненте нельзя, так как возникающая при этом погрешность умножается на волновое

число k = 2π/λ (λ = λсвета ≈ 1 мкм) и возникают большие фазовые погрешности).

Рисунок 1.6 − Зоны дифракции Фраунгофера и Френеля

Для получения более точного приближения представим r в виде

Считая величину [(x – x0)2 + (y – y0)2]/z2 малой, разложим квадратный корень в степенной ряд, воспользовавшись представлением (1 + α)0,5 = 1 + +α/2 − α2/8 + ...; |α| << 1. Учитывая первые два члена, получим следующее приближение:

Выражение (1.25) позволяет по известному распределению поля в плоскости z = 0 рассчитать амплитуду волны в произвольной точке

16

Введение в радиооптику

пространства (x,y,z) и носит название формулы дифракции Френеля. Погрешность фазовой аппроксимации экспоненты в (1.22) с учетом (1.23) не превосходит величины k[(x – x0)2 + (y – y0)2]2/8z3 поскольку степенной ряд знакопеременный. Если предположить, что эта фазовая погрешность не превосходит величину 2π × 0,1 (критерий Рэлея), то приближение Френеля справедливо в зоне

z ≥ [(Ra – ρн)4/λ]1/3, (1.26)

где Ra, ρн – максимальный радиус апертуры Σ и области наблюдения в плоскости z соответственно (см. рис. 1.6); λ – длина ЭМВ.

Приближение Фраунгофера. В случае, когда размеры источника излучения Σ малы, а расстояние z велико, в квадратичном множителе в экспоненте выражения (1.22) можно пренебречь членами второго порядка малости относительно переменныхx0 иу0. Тогда [(x – x0)2 + (y –y0)2]/2z≈ ≈ (x2 + y2)/2z – (xx0 + yy0)/z, а выражение (1.25) для поля в произвольной точке принимает вид

Последнее выражение носит название формулы дифракции Фраунгофера. Определим область (Фраунгофера), в которой справедливо приближенное выражение (1.27). Используя критерий Рэлея, получаем, что допустимая погрешность по фазе будет 0,5kRa2/z ≤ 2π×0,1, где Ra

– максимальный радиус апертуры Σ (см. рис. 1.6), откуда 4Ra2/2z ≤ 0,8z. Полагая Da = 2Ra, заменяя коэффициент 0,8 на 1, окончательно запишем z ≥ Da2/λ. (1.28)

Для анализа выражений (1.28) и (1.26) перепишем их относительно размеров 2ρн областей Фраунгофера и Френеля (при заданных z и

λ), т.е.:

Так как z >> λ, то получаем, что область Френеля шире области Фраунгофера (см. рис. 1.6) [4, 8].

Для оценки расстояний z для формул дифракции Френеля и Фраунгофера положим, что в оптическом диапазоне волн λ = 1 мкм = 10–6 м, Da = 2Ra = 1 мм = 10–3м. Тогда дифракция Френеля будет выполняться на расстоянии z ≥ (Da4/λ)1/3 = 10–2 м = 1 см, а дифракция Фраунгофера – только на расстоянии z ≥ Da2/λ = 1 м. Если размер апертуры и области наблюдения увеличить в 10 раз и принять Da = 1 см, то эти расстояния

17

Г.Г. Червяков, В.В. Роздобудько

составят соответственно 20 см и 100 м. Из этого примера видно, что в оптическом диапазоне приближением Фраунгофера можно пользоваться только при больших расстояниях z, Для сантиметрового диапазона радиоволн возьмем Da = 1 см, λ = 3 см. Дифракция Френеля будет при z ≥ 10 м, а дифракция Фраунгофера при z ≥ 30 м.

1.6 Импульсный отклик и передаточная функция слоя пространства Импульсный отклик. Рассмотрим выражение (1.22), позволяющее по известному распределению поля во входной плоскости z = 0 (см.

рис. 1.6) рассчитать амплитуду волны в произвольной точке пространства (x,y,z). Поскольку cosθzr/r = z/r2, (1.22) имеет вид интеграла свертки [4], то импульсный отклик слоя пространства будет

hs = kz exp[ik(x2 + y2 + z2)0,5]/[2iπ(x2 + y2 + z2)]. (1.31)

Рассмотрим далее формулы дифракции Френеля (1.25) и Фраунгофера (1.27) с позиций теории линейных инвариантных пространственных систем. Сопоставление (1.25) с интегралом суперпозиции для инвариантной системы [4] показывает, что поля во входной и выходной плоскостях системы связаны между собой соотношением типа свертки

где hϕ = 0,5k exp(ikz)exp[0,5ik(x 2 + y2 )/z]/izπ − импульсный отклик свободного пространства в области Френеля.

−∞

Из сопоставления (1.33) с (1.4) видно, что с точностью до амплитудного и фазового множителей, которые не зависят от (х0,у0), поле U(x,y,z) в выходной плоскости можно найти как Фурье-образ функции U0 (x0 ,y0 )exp[0,5ik(x02 +y02 ) / z] относительно пространственных частот νx =

=x/λz, νy = y/λz.

Далее, из сравнения (1.4) и (1.27), следует, что с точностью до стоящего перед интегралом в (1.27) множителя распределение амплитуды ЭМП в зоне дифракции Фраунгофера представляет собой Фурье-образ распределения поля во входной плоскости z = 0 (см. рис. 1.6):

18

Введение в радиооптику

U(x, y,z) 0,5kexp(ikz)exp[0,5ik(x2 +y2 )/ z]/iπz×

Прежде чем перейти к определению передаточной функции слоя пространства для общего случая (1.22) и приближения Френеля (1.32), приведем основные сведения по плоским и сферическим волнам.

Плоские волны, распространяющиеся в пространстве под различными углами, выполняют роль базисных функций в представлении пространственных сигналов − аналогично временным гармоникам при разложении сигналов, меняющихся во времени. Сферические волны позволяют наглядно интерпретировать импульсные отклики слоя пространства.

Плоские и сферические волны. Комплексная амплитуда

U(x,y,z), описывающая любую из компонент U(x,y,z)= =Re[U(x,y,z)exp(−i2πν)] ЭМП, удовлетворяет волновому уравнению (1.6).

Наиболее простым решением этого уравнения является плоская

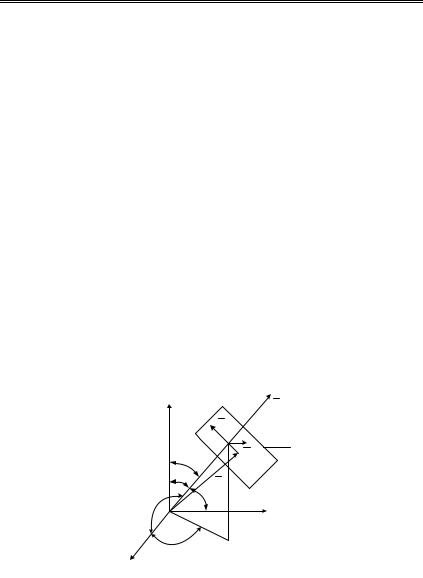
где U0 = const − амплитуда; k = − волновой вектоp, задающий направление распространения волны, в пространстве (рис. 1.7); kx = kcosα, ky =

=kcosβ, kz = kcosγ (cosα, cosβ, cosγ − направляющие косинусы вектора k, k = 2π/λ = 2πν/c); r = x0x +y0y + z0z − радиус-вектор точки, принадлежащей фронту плоской волны).

Рисунок 1.7 − Плоская ЭМВ

Раскрывая в (1.6) оператор Лапласа 2 в декартовой системе координат и подставляя (1.35), получаем следующую связь:

19

Г.Г. Червяков, В.В. Роздобудько

Поверхностьравных фазопределяется из соотношения xkx + уky + +zkz = c = const, которое задает уравнение плоскости, отсекающей на осях координат отрезки c/kx, c/ky, c/kz. Из полного комплексного представле-

ния плоской волны U(x,y,z,t) = U0exp[i(kxx + kyy + kzz) − ωt] следует, что с течением времени поверхность равных фаз перемещается параллельно самой себе, причем направление распространения ЭМВ определяется нормалью к волновой поверхности, которая, как известно, совпадает с grad c (c − константа, введенная выше и рассматриваемая как функция

x,y,z ). Поскольку gradc = x0∂c/∂x + y0∂c/∂y + z0∂c/∂z = x0kx + y0ky + z0kz, grad c = k, т.е. направление распространения действительно совпадает с

направлением волнового вектора.

Рассмотрим теперь сферические волны. Расписывая оператор Лапласа в (1.6) в сферической системе координат (r,θ,ϕ), получаем сле-

Поверхность равных фаз определяется из равенства kr=const=c следовательно, фронт волны − сфера r=const. Направление распростране-

ния волны определяется вектором grad c (x,y,z) = grad (kr) = kgrad(r). Так как r = (x2 + y2 + z2)0,5, то k grad(r) = k(x0x +y0y + z0z)/r = kr/r, т. е. волна распространяется вдоль радиуса-вектора r. Подставляя r = (x2 + y2 + z2)0,5

Так называемое параксиальное приближение следует из (1.38) в случае, когда z велико, а x и у малы. При этом в соответствии с (1.23), (1.24) имеем

Нетрудно видеть, что импульсный отклик свободного пространства, в приближении Френеля hϕ(х,у) (1.32), представляет собой сферическую волну в параксиальном приближении.

Определим теперь передаточной функции слоя пространства

Н(νх,νу).

Передаточная функция слоя пространства. Для определения передаточной функции слоя пространства можно использовать два подхода. Первый связан с понятием "угловой спектр плоских волн" и позволяет шире раскрыть физическое содержание процессов преобразования поля в слое пространства. Его здесь применим для определения передаточной функции слоя пространства Н(νх,νу) в общем случае скалярной теории дифракции (1.22), (1.31). Второй подход основан на использова-

20