Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Витебский государственный университет им. П. М. Машерова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Тер.вер(решение задач)

.pdf

Скачиваний:

502

Добавлен:

14.04.2015

Размер:

903.75 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 137 8 9 10 11 12 13 > Следующая >>>

= 14 54 56 + 34 15 16 = 16 + 401 = 12023 ;

P(x5 ) = P(X = 25) = P( A1 )P(A2 )P(A3 ) = 14 15 56 = 241 ; P(x6 ) = P(X = 35) = P( A1 )P(A2 )P(A3 ) = 14 54 16 = 301 ; P(x7 ) = P(X = 40) = P(A1 )P( A2 )P(A3 ) = 14 15 16 = 1201 .

Составим ряд распределения случайной величины Х – возможной суммы кредитов:


				xi						0					5				15				20		25		35		40
	pi = P(X = xi)											1				1					1			23		1		1		1
	pi = P(X = xi)									2					8				10				120		24		30		120
										2					8				10				120		24		30		120
Проверка: ∑pi		=	1	+	1	+		1	+		23		+	1	+		1	+		1		=1 .
Проверка: ∑pi		=	2	+	8	+	10		+	120			+	24	+		30	+	120			=1 .
			2		8		10			120				24			30		120

Математическое ожидание случайной величины X равно: mx = ∑xi pi = 12 0 + 18 5 +K+ 1201 40 = 8,5 .

Дисперсия случайной величины X равна:

D[X ] = M[ X 2 ] − mx2 = ∑xi2 pi − mx2 = =	1	02	+	1	52	+K+		1	402 −8,52 =
D[X ] = M[ X 2 ] − mx2 = ∑xi2 pi − mx2 = =	2	02	+	8	52	+K+	120		402 −8,52 =
	2			8			120
=182,5 −72,25 =110,25 .

Среднее квадратическое отклонение случайной величины X равно:

σx = D[ X ] = 110,25 =10,5

Задача 90. Случайная величина Х – годовой доход наугад взятого лица, облагаемого налогом. Ее плотность распределения имеет вид:

a , при x ≥ 5, f(х) = x3,1

0, при x < 5,

где a – неизвестный параметр. Требуется:

-определить значение параметра a ;

-найти функцию распределения F(х);

-определить математическое ожидание и среднее квадратическое отклонение;

-определить размер годового дохода хl, не ниже которого с вероятностью p = 0,5 окажется годовой доход случайно выбранного налогоплательщика;

-построить графики функций F(х) и f(х).

Решение.

Воспользуемся условием нормировки:

+∞∫ f (x)dx =1.

−∞

∫5

0 dx + +∞∫

dx =1, откуда a +∞∫x−3,1dx = a

x−2,1

5+∞ = 0 +

=1 ,

3,1

2,1

−∞

−2,1

2,1 5

следовательно, a = 52,1 2,1 = 61,667 . Итак,

324,1

при х ≥ 7,

(x) = x3,5

при х < 7.

Функция распределения

F(x) = ∫х

f (x)dx .

−∞

Для х < 5

F(x) = 0, т.к. при х < 5 f(x) = 0.

Для х≥5

F(x) = ∫x

f (x)dx

= ∫5

0 dx + ∫x

61,667

dx = 61,667 ∫x x−3,1dx = 61,667

x−2,1

x =1 −

129,64

3,1

− 2,1

2,5

−∞

Итак,

при х < 5,

129,5

F(x) =

−

при х ≥ 5.

2,1

mx =

+∞xf (x)dx = 5 x 0 dx +

+∞x

61,667

dx = 61,667

+∞x−

2,1dx = 61,667

x−1,1

+∞

−1,1

∫

x3,1

∫

−∞

= 0 +

61,667

≈ 9,545.

1,1

1,1 5

D[X ]= M [X 2 ]−mx2 = +∞∫x2 f (x)dx −mx2 ,

−∞

+∞

61,667

+∞

−0,1

+∞

∫x2 f (x)dx = ∫x2 0 dx +

∫x2

dx = 61,667

∫x−1,1dx = 61,887

3,1

−0,1

−∞

= 0 +

61,667

≈ 525 .

0,1 50,1

Следовательно,

Dx = M[X2] − m2x ≈ 525−(9,545)2 ≈ 433,884, σх = Dx ≈ 20,83.

Т.к. по определению

F(x) = P(X<x) и P(X<x) + P(X≥х) = 1, то P(X≥х) = 1-P(X<x) =1-F(x),

следовательно, P(X≥х1)=1−F(x1)=0,5; откуда F(x1) = 0,5.

1 −	61,667		= 0,5;		61,667		=1 − 0,5 = 0,5;	x2,1	=	61,667	≈123,335 .

	õ1	2,1		õ1		2,1		1	0,5

Чтобы найти х1, воспользуемся таблицами десятичных логарифмов:
x2,1	=123,335;			2,1 lgx1 = lg 123,335; 2,1 lgx1 = 2,0911; lg x =								2,0911		= 0,9958 .

1											1		2,1

По таблице антилогарифмов х1 ≈ 9,903.

Задача 91. Вероятность того, что саженец ели прижился, и будет расти, равна 0,8. Посажено 400 саженцев ели. Какова вероятность того, что нормально вырастут не менее 250 деревьев?

Решение.

Имеем схему Бернулли. Поскольку n p (1 − p) = 400 0,8 0,2 = 64 > 20 ,

то воспользуемся нормальным приближением. Если вероятность p наступления события A в каждом испытании постоянна и отлична от 0 и 1, то согласно интегральной теореме Муавра– Лапласа вероятность того, что число vn наступления события A в n независимых испытаниях заключено в пределах от c до d, приближенно равна:

Pn, p (c ≤ vn ≤ d )≈ Φ(t2 ) − Φ(t1 ) ,

c −np

d − np

e−

где t =

; t

; Φ(t) =

dx − функция Лапласа, значения которой

np(1− p)

np(1 − p)

2π −∫∞

определяются из таблиц.

Подставим исходные данные:

250 − 400 0,8

= −8,75 ,

400 0,8 0,2

400 − 400 0,8

=10 .

400 0,8 0,2

−8,75

e−

Φ(−8,75) =

∫

dx = 0 ,

2π

−∞

	1	10		x2
Φ(10) =		∫e−			dx =1.
				2
	2π −∞
P400;0,8 (250 ≤ vn			≤ 400)≈ Φ(10) − Φ(−8,75) =1 − 0 =1.

Задача 92. Завод получает сырье на автомашинах от трех независимо работающих поставщиков. Вероятность прибытия автомашины от первого поставщика равна 0,2, от второго

– 0,3, от третьего – 0,1. Составить распределение числа прибывших машин. Найти математическое ожидание и дисперсию полученной случайной величины. Построить график интегральной функции распределения.

Решение.

Очевидно, что случайная величина X – число прибывших машин может принимать четыре возможных значения – 0, 1, 2, 3. Найдем вероятности этих событий:

P(X = 0) = 0,8 0,7 0,9 = 0,504 ,

P(X =1) = 0,2 0,7 0,9 + 0,8 0,3 0,9 + 0,8 0,7 0,1 = 0,398 ,

P(X = 2) = 0,2 0,3 0,9 + 0,2 0,7 0,1+ 0,8 0,3 0,1 = 0,092 ,

P(X = 3) = 0,2 0,3 0,1 = 0,006 .

Закон распределения дискретной случайной величины X – числа прибывших машин имеет

вид:

xi	0	1	2	3
pi = P(X = xi)	0,504	0,398	0,092	0,006

Математическое ожидание случайной величины равно

M[X ] = ∑pi xi = 0,504 0 + 0,398 1+ 0,092 2 + 0,006 3 = 0,6 .

Дисперсия равна

D[ X ] = M[ X 2 ] − M[ X ]2 = ∑xi2 pi − ∑xi pi .

M[X 2 ] = 02 0,504 +12 0,398 + 22 0,092 +32 0,006 = 0,82 .

D[X ] = 0,82 −0,62 = 0,82 −0,36 = 0,46 .

График интегральной функции распределения случайной величины X, приведен на рис. 1.

Интегральная функция распределения

F (x )

0,8

		0,6
		0,6
		0,4


		0,2
		0,2
		0
		0
-2	-1	0	1	2	3	4	5 x 6

Рис. 1. График интегральной функции распределения случайной величины X.

Задача 93. Найти математическое ожидание и дисперсию случайной величины X, заданной плотностью распределения f(x). Найдите интегральную функцию распределения, постройте графики f(x), F(x).

0,		x ≤ 0,

f (x) =	x	, 0 < x ≤ 4,

8		x > 4.
0,

Решение.

Математическое ожидание случайной величины X равно

M[X ] =	∞∫xf (x)dx = ∫4			x2			dx =		x3		4	=		8	.

									24					3
	−∞	0			8						0

Дисперсия равна
D[X ] =	∞∫x2 f (x)dx = ∫4					x3		dx =		x4		4	= 8 .

					8
	−∞		0						32			0

Найдем интегральную функцию распределения F(x) = ∫−∞∞ f (x)dx .

x ≥ 0 : F(x) = 0 ,
0 < x ≤ 4 :	F(x) = ∫0x	x	dx =	x2	,

	8		16

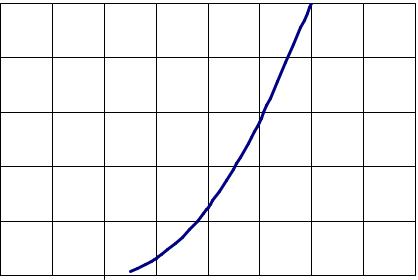
x > 4 : F(x) =1.

0,		x ≤ 0,
x2		, 0 < x ≤ 4,
F(x) =

16		x > 4.
1,

Интегральная функция распределения

F (x )

0,8

0,6

0,4

0,2

0 -2 -1 0 1 2 3 4 5 x 6

Задача 94. Случайная величина Х имеет распределение, заданное таблицей.

Xi	-2	0	4	5
pi	0,1	0,4	0,3	0,2

Составьте закон распределения, найдите математическое ожидание и дисперсию случайной величины: Z = (X – 1)2.

Решение.

Вначале зададим распределение случайной величины Y = X −1:

	Yi	-3	-1	3		4
	pi	0,1	0,4	0,3		0,2
Теперь зададим распределение случайной величины Z = Y 2					= ( X −1)2 :

Zi	1	9	16
pi	0,4	0,4	0,2

Поскольку z1 = z3 = 9 , то эти столбцы объединим, а вероятности данных значений сложим. В

результате получим следующее распределение случайной величины Z:

Математическое ожидание случайной величины Z равно:

μz = ∑zi pi =1 0,4 +9 0,4 +16 0,2 = 7,2 .

Дисперсия случайной величины Z равна:

σ2z = ∑(zi −μz )2 pi = (1 −7,2)2 0,4 + (9 −7,2)2 0,4 + (16 −7,2)2 0,2 =

=15,376 +1,296 +15,488 = 32,16 .

Задача 95. Вероятность поражения стрелком мишени равна p = 0,8 . Найти вероятность того, что при n =100 выстрелах мишень будет поражена ровно k = 86 раз. Решить, используя формулы Бернулли и Лапласа. Сделать выводы.

Решение.

По формуле Бернулли искомая вероятность равна

(86) = C86

p86 (1

− p)14

= C86

0,886 0,214

= 0,0022 .

100

Согласно локальной теореме Муавра–Лапласа

Pn, p (k)

≈

f (t)

np(1− p)

где f (t) =

e−

, t =

k −np .

2π

np(1− p)

Имеем:

86 −100 0,8 =

1,52

t =

=1,5 ;

f (1,5) =

e−

= 0,1295 ;

100 0,8 0,2

2π

(86) ≈

0,1295

= 0,1295 = 0,0324 .

100;0,8

100 0,8 0,2

Различие в ответах объясняется тем, что в данном случае использование формулы Бернулли приводит к большим вычислительным ошибкам.

Задача 96. По заданному закону распределения дискретной случайной величины X, найти ее среднее квадратическое отклонение, привести аналитическое и графическое изображение функции распределения F(x), построить многоугольник распределения вероятностей.

xi	12	16	21	26	30
pi	0,2	0,1	0,4	0,2	0,1

Решение.

Среднее квадратическое отклонение дискретной случайной величины X равно

σx = M[X 2 ] − mx2 ,

где M[X 2 ] = ∑xi2 pi =122 0,2 +... +302 0,1 = 456 ; mx = ∑xi pi =12 0,2 +... +30 0,1 = 20,6 .

Отсюда

σx = M[ X 2 ] − mx2 = 456 − 20,62 = 456 − 424,36 = 31,64 = 5,625 .

Функция распределения F(x) имеет вид

0,	x ≤12,
	12 < x ≤16,
0,2,	12 < x ≤16,
0,3,	16 < x ≤ 21,
F(x) =	21 < x ≤ 26,
0,7,	21 < x ≤ 26,
0,9,	26 < x ≤ 30,

	x > 30.
1	x > 30.

Задача 97. Вероятность поражения стрелком мишени равна

p = 0,5 . Найти вероятность

того, что при

n = 8 выстрелах мишень будет поражена от

= 5 до k2 = 7 раз. Решить,

используя формулы Бернулли и Лапласа. Сделать выводы.

Решение.

По формуле Бернулли искомая вероятность равна

P (5 ≤ m ≤ 7) = P (5) + P (6)

+ P (7)

= C 5 p5 (1

− p)3 +C 6 p6

− p)2 +C 7 p7 (1 − p)1 =

56 0,58 + 28 0,58

+8 0,58 =

56 + 28

= 0,3594 .

256

Согласно интегральной теореме Муавра–Лапласа

Pn, p (c ≤ vn ≤ d )→ Φ(t2 ) − Φ(t1 ) ,

где t = c −np

d −np

e−

, t

, Φ(t) =

− функция Лапласа, значения которой

np(1− p)

2π −∞∫

определяются из таблиц. Имеем:

c = k1 = 5 ; d = k2

= 7 ; t1 =

5 −8 0,5

≈ 0,7071; t2

7 −8 0,5

≈ 2,1213 ;

8 0,5 0,5

0,7071

e−

2,1213

e−

Φ(0,7071) =

∫

dx = 0,7602 ;

Φ(2,1213) =

∫

dx = 0,9830 ;

2π

−∞

2π

−∞

P8;0,5 (5 ≤ vn

≤ 7)≈ Φ(2,1213) − Φ(0,7071) = 0,9830 − 0,7602 = 0,2228 .

Различие в ответах объясняется тем, что число выстрелов слишком мало, чтобы пользоваться интегральной теоремой Муавра–Лапласа.

Задача 98. По заданному закону распределения дискретной случайной величины X, найти ее среднее квадратическое отклонение, привести аналитическое выражение для функции распределения F(x).

xi	15	19	24	29	30
pi	0,1	0,2	0,2	0,1	0,4

Решение.

Среднее квадратическое отклонение дискретной случайной величины X равно

σx = M[X 2 ] − mx2 ,

где M[X 2 ] = ∑xi2 pi =152 0,1 +... + 302 0,4 = 654 ; mx = ∑xi pi =15 0,1 +... +30 0,4 = 25 .

Отсюда

σx = M[ X 2 ] − mx2 = 654 − 252 = 654 − 625 = 29 = 5,385 .

Функция распределения F(x) имеет вид

0,	x ≤15,
	15 < x ≤19,
0,1,	15 < x ≤19,
0,3,	19 < x ≤ 24,
F(x) =	24 < x ≤ 29,
0,5,	24 < x ≤ 29,
0,6,	29 < x ≤ 30,

	x > 30.
1	x > 30.

Задача 99. Выход молодняка в инкубаторе составляет в среднем 75% числа заложенных яиц. Оценить вероятность того, что из 8000 заложенных в инкубатор яиц вылупится от 5950 до 6050 (включительно) яиц.

Решение.

Согласно интегральной теореме Муавра–Лапласа

Pn, p (c ≤ vn ≤ d )→ Φ(t2 ) − Φ(t1 ) ,

где t = c −np

d −np

, t

, Φ(t) =

e−

− функция Лапласа, значения которой

np(1− p)

2π −∞∫

определяются из таблиц. Имеем:

c = 5950 ; d = 6050 ; t1 = 5950 −8000 0,75

≈ −1,291 ;

6050 −8000 0,75

≈1,291;

8000 0,75 0,25

−1,291

e−

1,291

e−

Φ(−1,291) =

∫

dx = 0,0984 ;

Φ(1,291) =

∫

dx = 0,9016 ;

2π

−∞

2π

−∞

P8000;0,75 (5950 ≤ vn ≤ 6050)≈ Φ(1,291) − Φ(−1,291) = 0,9016 − 0,0984 = 0,8033 .

Задача 100. База отправила в магазин 500 изделий, вероятность повреждения изделия в пути 0,002. Найти вероятность того, что в пути будут повреждены 5 изделий.

Решение.

По условию n = 500 – велико, p = 0,002 – мало, поэтому воспользуемся пуассоновским приближением. Имеем λ = np = 500 0,002 = 1, k = 1. Следовательно, искомая вероятность равна,

Р500; 0,002(5) ≈	15	e−1	=	1	≈ 0,003.
	5!			5!e

Задача 101. В некоторой местности из каждых 100 семей 80 имеют холодильники. Найти:

1)вероятность того, что из 400 семей 300 имеют холодильники.

2)вероятность того, что от 300 до 360 (включительно) семей из 400 имеют холодильники.

Решение.

1) Вероятность того, что семья имеет холодильник, равна p = 80/100 = 0,8. Отсюда, используя локальную формулу Муавра–Лапласа, получим

t =	300 −400 0,8	= −2,5 ,	f (t) = f (−2,5) =	1	e−	2,52	≈ 0,0175 ,
						2
	400 0,8 0,2			2π

<<< < Предыдущая 1 2 3 4 5 67 / 137 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.03.2016232.96 Кб51Теория муз. дела.doc
#
11.11.20193.1 Mб16ТЕОРИЯ ПРИНЯТИЯ РЕШЕНИЙ_ред.doc
#
04.05.20192.67 Mб45Теория финансов-лекции.doc
#
02.09.201942.24 Кб9теория фирмы, издержки.docx
#
21.12.20181.05 Mб8Теория_и_история_источниковеденя_(дапаможн_к)[1....doc
#
14.04.2015903.75 Кб502Тер.вер(решение задач).pdf
#
24.09.2019285.9 Кб6термодинамика.docx
#
02.09.2019110.59 Кб4Территор общ самоупр Иные формы местн самоупр.doc
#
14.04.2015250.37 Кб916тест по криминалистике с решением.doc
#
14.04.2015145.41 Кб127Тест по Маторовой.doc
#
17.11.2019477.7 Кб6Тест по Угол. пр. общ.ч..doc