
Тер.вер(решение задач)
.pdf
|
Предельная ошибка выборки вычисляется по формуле = t |
σ |
|
|
= t σx |
. Она равна: |
||||||
|
x |
|||||||||||
|
|
|
|
|
|
|
|
n |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
для доверительной вероятности p = 68% |
= t |
sx |
= t0,16 (30) 8,143 = 2,142 ; |
|
|||||||
|
|
|
n |
|
|
30 |
|
|
|
|
||
- |
для доверительной вероятности p = 95% |
= t |
sx |
= t0,025 (30) |
8,143 = 3,508 |
; |
||||||
|
|
|
n |
|
|
30 |
|
|
|
|||
- |
для доверительной вероятности p = 99,7% |
= t sx |
= t0,0015 (30) |
8,143 |
= 5,195 . |
|||||||
|
|
|
|
n |
|
|
|
|
30 |
|
|
|
|
Доверительный интервал для генерального среднего: |
|
|
|
|
|
|
|
||||
- для доверительной вероятности p = 68% 13,424 < μx |
<17,709 ; |
|
|
|
|
|
|
|
||||
- |
для доверительной вероятности p = 95% 12,058 < μx |
<19,075 ; |
|
|
|
|
|
|
|
|||
-для доверительной вероятности p = 99,7% 10,371 < μx < 20,762 .
Доверительный интервал для генеральной дисперсии определяется по формуле
|
|
(n −1)s2 |
2 |
(n −1)s2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
< σx < |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
χ2 |
χ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
1−p |
|
1+ p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Квантиль распределения Пирсона: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
- |
для вероятности p = 68% χ12−p |
= χ12−0,68 |
= 36,480 ; χ12+ p |
= χ12+0,68 |
= 21,507 ; |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
|
||||||
- |
для вероятности p = 95% χ12−p |
= χ12−0,95 |
= 45,722 ; χ12+ p |
= χ12+0,95 |
=16,047 ; |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
|
||||||
- |
для вероятности p = 99,7% χ12−p = χ12−0,68 = 36,480 ; χ12+ p = χ12+0,68 = 21,507 . |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
|
2 |
|
|
|||||||||
Доверительный интервал для генеральной дисперсии равен:
-для доверительной вероятности p = 68% 52,724 < σ2x < 89,428 ;
- |
для доверительной вероятности p = 95% 42,066 < σ2x <119,858 ; |
|||||
- |
для доверительной вероятности p = 99,7% 33,836 < σ2x <167,690 . |
|||||
|
Доверительный интервал для генерального с.к.о. определяется по формуле |
|||||
|
s (n −1) < σx < s |
n −1 . |
||||
|
χ2 |
χ2 |
||||
|
1−p |
1+ p |
||||
|
|
2 |
|
|
2 |
|
Подставив квантили распределения Пирсона получим доверительный интервал для генерального с.к.о.:
- |
для доверительной вероятности p = 68% |
13,879 < σx <18,076 ; |
- |
для доверительной вероятности p = 95% |
12,397 < σx < 20,927 ; |

-для доверительной вероятности p = 99,7% 11,119 < σx < 24,752 .
Задача 140. Постройте доверительные интервалы для генерального среднего μx μy и μz при доверительной вероятности p = 68%; 95%; 99,7% упрощенным способом: «одна/две/три сигмы».
Решение.
Решение для выборки X.
Величину коэффициента t можно приближенно выбрать для стандартных значений вероятности (табл.8). Для этого используются процентные точки стандартной функции нормального распределения с нулевым средним и единичной дисперсией
|
Стандартные квантили нормального распределения |
Таблица 8 |
|||||||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Вероятность |
Вероятность |
Коэффициент |
Ошибка |
Доверительный |
|||||||
(округленно) |
доверия |
выборки |
интервал |
||||||||
|
|||||||||||
68% |
0,682689 |
1,000 |
одна сигма |
μ = |
|
|
|
± σ |
|||
x |
|||||||||||
95% |
0,954500 |
2,000 |
две сигмы |
μ = |
|
|
|
|
± 2σ |
||
x |
|||||||||||
99,7% |
0,997300 |
3,000 |
три сигмы |
μ = |
|
|
|
±3σ |
|||
x |
|||||||||||
Таким образом, получаем доверительных интервалов: - p = 68%; x −σx < μ < x + σx ;
-p = 95%; x − 2σx < μ < x + 2σx ;
-p = 99,7%; x −3σx < μ < x +3σx .
Отсюда с учетом того, что σ |
|
|
= σx |
= 15,567 =1,487 , получим доверительные |
|
x |
|||||
|
n |
30 |
|||
|
|
|
|||
интервалы для генерального среднего µx:
- для доверительной вероятности p = 68% 14,080 < μx <17,054 ;
-для доверительной вероятности p = 95% 12,593 < μx <18,540 ;
-для доверительной вероятности p = 99,7% 11,106 < μx < 20,027 .
Задача 141. При уровне значимости α = 32%; 5%; 0,3% проверьте гипотезы:
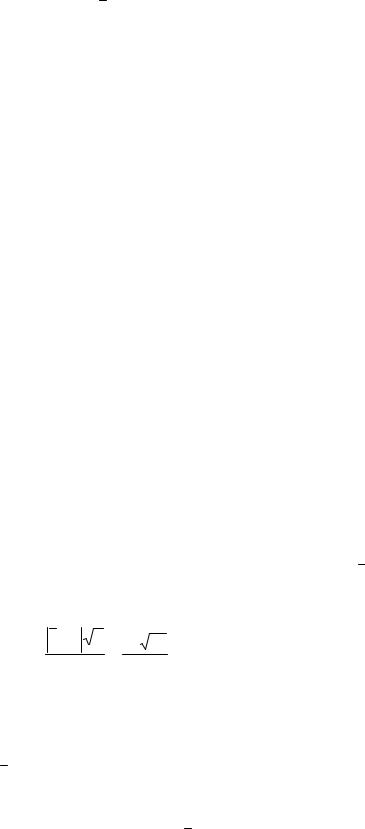
1) σ2x = σ2y ; 2) μx = x + 5 ; 3) μx = μy .
Решение.
1. Расчетное значение критической статистики при неизвестных математических ожиданиях определяется из выражения
|
|
|
|
|
|
|
|
|
|
1 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑1 |
(xi − |
|
|
)2 |
|
|
|
|
||
|
|
|
|
s |
2 |
|
|
|
|
|
x |
|
|
|
|||||||
|
|
|
|
|
|
|
n |
−1 |
66,323 |
|
|
||||||||||
|
|
|
|
x |
|
|
|
= |
|
|
|
|
|
|
|
|
|||||
ψ |
расч |
= |
|
= |
|
1 |
|
|
i 1 |
|
|
|
= |
|
= 0,094 . |
|
|||||
|
2 |
|
|
|
|
|
n |
|
|
|
702,148 |
|
|||||||||
|
|
|
|
sy |
1 |
|
∑2 |
( yi − |
|
)2 |
|
|
|||||||||
|
|
|
|
|
y |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
n2 |
−1 i=1 |
|
|
|
|
|
|
|
|
|
|||
Если выполняется условие |
|
|
|
|
|
|
|
|
|
||||||||||||
F1− |
α (n1 −1, n2 |
|
−1) ≤ ψðàñ÷ ≤ Fα (n1 −1, n2 −1) , |
(1) |
|||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
то гипотеза σ2x = σ2y |
принимается на уровне значимости α. |
||||||||||||||||||||
При α = 32%: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
F1− |
α (n1 −1, n2 |
|
−1) = F0,68 (29;29) = 0,839 , Fα (n1 −1, n2 |
−1) = F0,16 (29;29) =1,453. |
|||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
Т.к. условие (1) не выполняется, то гипотеза σ2x = σ2y |
на уровне значимости α = 32% не |
||||||||||||||||||||
принимается.
Поскольку вероятности 5%; 0,3% меньше чем 32%, то, очевидно, что и на уровнях значимости α = 5%, α = 0,3% гипотеза σ2x = σ2y также не принимается.
2. Проверим гипотезу о среднем значении: μx = a = x + 5 = 20,567 .
Расчетное значение статистики равно
t расч = |
x − a n |
= |
5 30 = 3,363 . |
|
s |
|
8,144 |
Пусть α = 32%. |
Критическое значение статистики равно tкр = tα (n −1) = t0,16 (29) =1,442 . |
||
|
|
|
2 |
Поскольку |
расчетное |
значение статистики больше критического значения, то гипотеза |
|
μx = x + 5 на уровне значимости α = 32% не принимается.
Т.к. вероятности 5%; 0,3% меньше чем 32%, то, очевидно, что и на уровнях значимости
α = 5%, α = 0,3% гипотеза μx = x + 5 также не принимается. 3. Проверим гипотезу о равенстве средних μx = μy .
Расчетное значение статистики равно

t расч = |
|
|
x |
− |
y |
|
|
= |
15,567 + 47,3 |
=12,421. |
|||||||
|
sx2 |
|
|
|
|
|
66,323 |
|
|
702,148 |
|||||||
|
|
+ |
sy2 |
|
+ |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
30 |
|
30 |
|
||||
|
|
n1 |
n2 |
|
|||||||||||||
Критическое значение статистики равно tкр = tα / 2 (n −1) = t0,16 (29) =1,442 . |
|||||||||||||||||
Поскольку |
расчетное |
значение |
статистики больше критического значения, то гипотеза |
||||||||||||||
μx = μy на уровне значимости α = 32% не принимается.
Т.к. вероятности 5%; 0,3% меньше чем 32%, то, очевидно, что и на уровнях значимости
α = 5%, α = 0,3% гипотеза μx = μy также не принимается.
Задача 142. Вычислите линейные коэффициенты корреляции ryx и rzx. Сделайте вывод о тесноте линейной связи между признаками.
Решение.
Расчеты выполним для коэффициента корреляции ryx.
Линейный коэффициент корреляции вычисляется следующим образом:
|
n |
|
|
|
|
rxy = |
∑(xi − x)( yi − y) |
. |
|||
i=1 |
|
|
|
||
|
|
|
|
||
|
n |
n |
|
||
|
∑(xi |
− x)2 |
|
∑( yi − y)2 |
|
i=1 |
|
i=1 |
|
||
Подставив исходные данные, получим rxy = −0,973 .
Проверим значимость статистической связи. Расчетное значение статистики равно
t расч = r n − 2 = |
0,973 28 = 96,50 . |
1 − r 2 |
1 −0,9732 |
Критическая статистика равна tα (n − 2) = t0,025 (28) = 2,368 .
2
Поскольку расчетное значение статистики больше критического значения, то на уровне значимости α = 5% считаем, что между признаками X и Y имеет место отрицательная линейная статистическая связь.
Задача 143. Вычислите коэффициенты корреляции рангов Спирмена и Кендалла Y(X) и Z(X). Сделайте вывод о тесноте связи.
Решение.
Расчеты выполним для коэффициентов корреляции рангов Спирмена и Кендалла Y(X). Коэффициент ранговой корреляции Спирмена между переменными X и Y находится по
формуле
|
|
|
6 |
n |
|
ρx / y =1− |
|
|
∑(ri −si )2 . |
(2) |
|
n |
3 |
|
|||
|
|
−n i=1 |
|
||
где ri и si − ранги i-го объекта по переменным X и Y, n − число пар наблюдений. Составим таблицу:
|
|
|
|
|
Таблица 9 |
|
|
|
|
|
|
|
|
N |
X |
Y |
r |
s |
|
(ri - si)2 |
|
|
|
|
|
|
|
1 |
12 |
-41 |
11,5 |
16 |
|
20,25 |
2 |
14 |
-37 |
15,5 |
18 |
|
6,25 |
3 |
8 |
-10 |
8 |
29,5 |
|
462,25 |
4 |
24 |
-72 |
23 |
9,5 |
|
182,25 |
5 |
3 |
-10 |
1,5 |
29,5 |
|
784 |
6 |
7 |
-19 |
5,5 |
24 |
|
342,25 |
7 |
8 |
-20 |
8 |
23 |
|
225 |
8 |
19 |
-62 |
19,5 |
12 |
|
56,25 |
9 |
19 |
-64 |
19,5 |
11 |
|
72,25 |
10 |
26 |
-78 |
26,5 |
4,5 |
|
484 |
11 |
22 |
-77 |
21 |
6 |
|
225 |
12 |
26 |
-83 |
26,5 |
2 |
|
600,25 |
13 |
14 |
-42 |
15,5 |
15 |
|
0,25 |
14 |
26 |
-86 |
26,5 |
1 |
|
650,25 |
15 |
5 |
-14 |
3,5 |
25,5 |
|
484 |
16 |
13 |
-28 |
14 |
22 |
|
64 |
17 |
8 |
-36 |
8 |
19,5 |
|
132,25 |
18 |
27 |
-75 |
29 |
8 |
|
441 |
19 |
12 |
-36 |
11,5 |
19,5 |
|
64 |
20 |
12 |
-31 |
11,5 |
21 |
|
90,25 |
21 |
25 |
-76 |
24 |
7 |
|
289 |
22 |
17 |
-56 |
18 |
13,5 |
|
20,25 |
23 |
12 |
-40 |
11,5 |
17 |
|
30,25 |
24 |
28 |
-78 |
30 |
4,5 |
|
650,25 |
25 |
7 |
-13 |
5,5 |
27 |
|
462,25 |
26 |
3 |
-14 |
1,5 |
25,5 |
|
576 |
27 |
5 |
-11 |
3,5 |
28 |
|
600,25 |
28 |
16 |
-56 |
17 |
13,5 |
|
12,25 |
29 |
23 |
-72 |
22 |
9,5 |
|
156,25 |
30 |
26 |
-82 |
26,5 |
3 |
|
552,25 |
Σ |
- |
- |
- |
- |
|
8735 |
Тогда по формуле (2) имеем: ρx / y |
= −0,9433. |
|||
Коэффициент ранговой корреляции Кендалла между переменными X и Y находится по |
||||
формуле: |
|
|
|
|
τx / y =1− |
4K |
, |
(3) |
|
n(n −1) |
||||
|
|
|
||
где K – статистика Кендалла, представляющая собой минимальное число обменов между элементами последовательности s, необходимое для приведения ее к упорядочиванию, аналогичному последовательности r.
Для определения статистики K необходимо ранжировать объекты по одной переменной (пусть, для определенности по X) в порядке возрастания (при этом ее ранги будут упорядочены ( r1 ≤ r2 ≤K≤ rn ) и определить соответствующие им ранги si, i = 1, … , n,
переменной Y. Статистика K равна общему числу инверсий (нарушений порядка, когда большее число стоит слева от меньшего), в ранговой последовательности s1 , s2 ,K, sn .
Результаты расчетов приведены в табл. 10.
|
|
|
|
Таблица 10 |
|
|
|
|
|
X |
Y |
r |
s |
Число инверсий K |
3 |
-10 |
1 |
29 |
28 |
3 |
-14 |
1 |
25 |
24 |
5 |
-14 |
3 |
25 |
24 |
5 |
-11 |
3 |
28 |
25 |
7 |
-19 |
5 |
24 |
23 |
7 |
-13 |
5 |
27 |
23 |
8 |
-10 |
7 |
29 |
23 |
8 |
-20 |
7 |
23 |
22 |
8 |
-36 |
7 |
19 |
18 |
12 |
-41 |
10 |
16 |
16 |
12 |
-36 |
10 |
19 |
17 |
12 |
-31 |
10 |
21 |
17 |
12 |
-40 |
10 |
17 |
15 |
13 |
-28 |
14 |
22 |
16 |
14 |
-37 |
15 |
18 |
15 |
14 |
-42 |
15 |
15 |
14 |
16 |
-56 |
17 |
13 |
12 |
17 |
-56 |
18 |
13 |
12 |
19 |
-62 |
19 |
12 |
11 |
19 |
-64 |
19 |
11 |
10 |
22 |
-77 |
21 |
6 |
5 |
23 |
-72 |
22 |
9 |
7 |

|
|
24 |
|
-72 |
23 |
9 |
7 |
|
|
25 |
|
-76 |
24 |
7 |
5 |
|
|
26 |
|
-78 |
25 |
4 |
3 |
|
|
26 |
|
-83 |
25 |
2 |
1 |
|
|
26 |
|
-86 |
25 |
1 |
0 |
|
|
26 |
|
-82 |
25 |
3 |
1 |
|
|
27 |
|
-75 |
29 |
8 |
1 |
|
|
28 |
|
-78 |
30 |
4 |
1 |
|
|
Σ |
|
- |
- |
- |
396 |
Сумма всех инверсий: K = 396. Теперь по (3) |
|
||||||
τx / y =1 − |
4 396 |
= −0,821. |
|
|
|
||
30(30 −1) |
|
|
|
||||
|
|
|
|
|
|
||
Большие по величине значения ранговых коэффициентов корреляции свидетельствуют о наличии тесной связи между признаками X и Y.
Задача 144. Постройте уравнения регрессии Y(X), Z(X) графическим способом.
Решение.
Расчеты выполним для уравнения регрессии Y(X).
При построении линии регрессии на корреляционном поле проводят линию регрессии с помощью линейки, «на глаз» - по местам «сгущения» точек. Отдельные точки, далеко отстоящие от «облака рассеяния» (аномальные данные), игнорируют (рис.4). На линии регрессии выбирают две точки, ближе к краям диапазона значений. Это точки M1 (5; −14) и
M 2 (26; −82) . Составляем систему уравнений – два уравнения с двумя неизвестными:
a +5b = −14,a + 26b = −82.
Решая систему, получаем оценки неизвестных коэффициентов: a = 2,190 , b = −3,238 . |
|
В результате имеем эмпирическое уравнение регрессии |
|
y(x) = 2,190 −3,238x . |
(4) |
Задача 145. С помощью метода наименьших квадратов (МНК) постройте уравнения регрессии Y(X), X(Y), Z(X), X(Z). Нанесите линии регрессии на корреляционное поле.

Решение.
Расчеты выполним для уравнения регрессии Y(X)
y(x) = b0 + b1 x .
Коэффициенты регрессии b0, b1 находим методом наименьших квадратов, решая систему линейных уравнений
b0 n +b1 ∑xi = ∑yi ,b0 ∑xi +b1 ∑xi2 = ∑yi xi ,
где n = 30.
Для расчета выполним предварительные вычисления, которые приведены в табл. 11.
|
|
|
|
|
Таблица 11 |
||
|
|
|
|
|
|
|
|
i |
xi |
yi |
xi2 |
xiyi |
|
y)i |
|
1 |
12 |
-41 |
144 |
-492 |
|
-36,009 |
|
2 |
14 |
-37 |
196 |
-518 |
|
-42,34 |
|
3 |
8 |
-10 |
64 |
-80 |
|
-23,346 |
|
4 |
24 |
-72 |
576 |
-1728 |
|
-73,998 |
|
5 |
3 |
-10 |
9 |
-30 |
|
-7,5171 |
|
6 |
7 |
-19 |
49 |
-133 |
|
-20,18 |
|
7 |
8 |
-20 |
64 |
-160 |
|
-23,346 |
|
8 |
19 |
-62 |
361 |
-1178 |
|
-58,169 |
|
9 |
19 |
-64 |
361 |
-1216 |
|
-58,169 |
|
10 |
26 |
-78 |
676 |
-2028 |
|
-80,329 |
|
11 |
22 |
-77 |
484 |
-1694 |
|
-67,666 |
|
12 |
26 |
-83 |
676 |
-2158 |
|
-80,329 |
|
13 |
14 |
-42 |
196 |
-588 |
|
-42,34 |
|
14 |
26 |
-86 |
676 |
-2236 |
|
-80,329 |
|
15 |
5 |
-14 |
25 |
-70 |
|
-13,849 |
|
16 |
13 |
-28 |
169 |
-364 |
|
-39,175 |
|
17 |
8 |
-36 |
64 |
-288 |
|
-23,346 |
|
18 |
27 |
-75 |
729 |
-2025 |
|
-83,495 |
|
19 |
12 |
-36 |
144 |
-432 |
|
-36,009 |
|
20 |
12 |
-31 |
144 |
-372 |
|
-36,009 |
|
21 |
25 |
-76 |
625 |
-1900 |
|
-77,164 |
|
22 |
17 |
-56 |
289 |
-952 |
|
-51,838 |
|
23 |
12 |
-40 |
144 |
-480 |
|
-36,009 |
|
24 |
28 |
-78 |
784 |
-2184 |
|
-86,661 |
|
25 |
7 |
-13 |
49 |
-91 |
|
-20,18 |
|
26 |
3 |
-14 |
9 |
-42 |
|
-7,5171 |
|
27 |
5 |
-11 |
25 |
-55 |
|
-13,849 |
|
28 |
16 |
-56 |
256 |
-896 |
|
-48,672 |
|
|
|
|
|
|
|
|
29 |
|
|
|
|
23 |
|
|
|
-72 |
|
529 |
-1656 |
|
-70,832 |
|
|
|||||||
|
|
|
|
|
|
|
30 |
|
|
|
|
26 |
|
|
|
-82 |
|
676 |
-2132 |
|
-80,329 |
|
|
|||||||
|
|
|
|
|
|
Всего |
|
|
467 |
|
|
-1419 |
|
9193 |
-28178 |
-1419 |
|
|
||||||||||||
|
|
|
|
|
|
Среднее |
15,5667 |
|
-47,3 |
|
306,433 |
-939,27 |
-47,3 |
|
|
|||||||||||||||
Решение данной системы имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
n∑xi yi |
|
∑xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
− |
|
|
∑yi |
30 (−28178) − 467 (−1419) |
|
|
|
|
||||||||||||||||||||
b |
= |
|
i |
|
i |
|
|
|
|
i |
|
= |
|
= −3,166 , |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
30 9193 − 4672 |
|
|
|
|
|
|
||||||||
|
|
|
n∑xi2 − |
∑xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
i |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
∑yi −b1 ∑xi |
|
1 |
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
3,166 |
|
|
|
|||||||
b0 |
|
|
= |
∑yi − |
∑xi = y −b1 x = −47,3 + |
15,567 |
=1,980 . |
|||||||||||||||||||||||
= |
|
i |
i |
|
|
|
1 |
|
|
|
|
|||||||||||||||||||
|
n |
|
|
|
|
n |
n |
|
30 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
i |
|
|
|
i |
|
|
|
|
|
|
|
|
|
||||||||
Таким образом, линейная однопараметрическая модель регрессии показателя y от x имеет вид:
y(x) =1,980 −3,166x . |
|
|
|
|
|
|
|
|
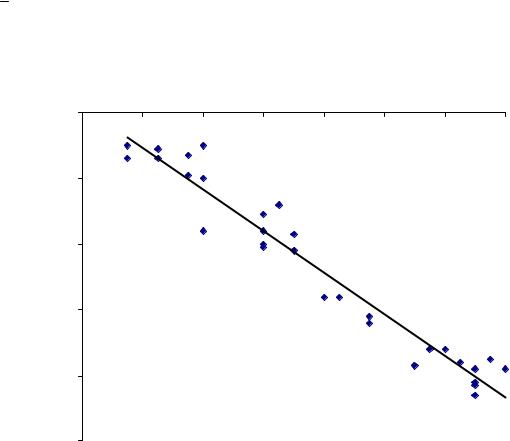
Нанесем линии регрессии на корреляционное поле (рис. 6). |
|
|
|
|||||
0 |
|
|
|
|
|
|
|
x |
0 |
4 |
8 |
12 |
16 |
20 |
24 |
28 |
|
-20 |
|
|
|
|
|
|
|
|
-40 |
|
|
|
|
|
|
|
|
-60 |
|
|
|
|
|
|
|
|
-80 |
|
|
|
|
|
|
|
|
-100 |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
Рис. 6. Корреляционное поле с нанесенной линией регрессии. |
|
|
||||||
