
Тер.вер(решение задач)
.pdf
(x1 − 3,5)2 = 02,5 = 0,25 ,
откуда
x1 − 3,5 = ± 0,25 = ±0,5 , или x1 = 3,5 ± 0,5 .
0,25 = ±0,5 , или x1 = 3,5 ± 0,5 .
С учетом того, что по условию x1 < x2, получим x1 = 3,5 − 0,5 = 3 ; x2 = 7 − x1 = 7 − 3 = 4 .
В результате получим закон распределения случайной величины X:
xi |
3 |
4 |
pi |
0,5 |
0,5 |
Задача 82. Известны математическое ожидание a и среднее квадратическое отклонение σ нормально распределенной случайной величины X. Найти вероятность попадания этой величины в заданный интервал (α; β), если a = 8; σ = 1; α = 4; β = 9.
Решение.
Приведем исходную случайную величину к стандартному виду, т.е. с нулевым математическим ожиданием и единичной дисперсией. В результате получим:
|
α − a |
|
X − a |
|
β − a |
|
4 −8 |
|
X −8 |
|
9 −8 |
|
|||
P(α ≤ X < β) = P |
|
≤ |
|
< |
|
|
= P |
|
≤ |
|
< |
|
|
= P(−4 ≤ Y <1) , |
|
σ |
σ |
σ |
1 |
1 |
1 |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||
где Y − стандартная нормально распределенная случайная величина с нулевым математическим ожиданием и единичной дисперсией.
Отсюда имеем
P(α ≤ X < β) = P(−4 ≤ Y <1) = F0 (1) − F0 (−4) = 0,5 + Φ(1) −[0,5 −Φ(4)] = Φ(1) + Φ(4) = = 0,341345 + 0,499968 = 0,841313 ≈ 0,8413 ,
где Φ( ) – функция Лапласа, табличные значения которой приведены в приложениях учебников по теории вероятностей и математической статистике.
Задача 83. Команда состоит из двух стрелков. Числа очков, выбиваемых каждым из них при одном выстреле, являются случайными величинами X1 и X2, которые характеризуются следующими законами распределения:
X1 |
3 |
4 |
5 |
P |
0,3 |
0,4 |
0,3 |
X2 |
2 |
3 |
4 |
5 |
P |
0,2 |
0,1 |
0,2 |
0,5 |
Результаты стрельбы одного стрелка не влияют на результаты стрельбы другого. Составить закон распределения числа очков, выбиваемых командой, если стрелки сделают по одному выстрелу. Убедиться в справедливости равенства D( X1 + X 2 ) = D( X1 ) + D( X 2 ) .
Решение.
1) Поскольку результаты стрельбы одного стрелка не влияют на результаты стрельбы другого, то случайные величины X1 и X2 являются независимыми. Поэтому
P(X1 = x1 , X 2 = x2 ) = P(X1 = x1 )P( X 2 = x2 ) .
Случайная величина Y = X1 + X 2 |
может принимать значения: 5, 6, 7, 8, 9, 10. |
||
Соответствующие вероятности равны: |
|
||
P(Y = 5) = P( X1 |
= 3)P( X 2 |
= 2) = 0,3 0,2 = 0,06 ; |
|
P(Y = 6) = P( X1 |
= 3)P( X 2 |
= 3) + P(X1 |
= 4)P( X 2 = 2) = 0,3 0,1 + 0,4 0,2 = 0,11; |
P(Y = 7) = P(X1 = 3)P(X 2 = 4) + P( X1 = 4)P(X 2 = 3) + P( X1 = 5)P( X 2 = 2) = |
|||
= 0,3 0,2 + 0,4 0,1+ 0,3 0,2 = 0,16 ; |
|
||
P(Y = 8) = P( X1 |
= 3)P(X 2 |
= 5) + P( X1 = 4)P(X 2 = 4) + P(X1 = 5)P(X 2 = 3) = |
|
= 0,3 0,5 + 0,4 0,2 + 0,3 0,1 = 0,26 ; |
|
||
P(Y = 9) = P( X1 |
= 4)P(X 2 |
= 5) + P( X1 |
= 5)P( X 2 = 4) = 0,4 0,5 + 0,3 0,2 = 0,26 ; |
P(Y =10) = P( X1 = 5)P( X 2 = 5) = 0,3 0,5 = 0,15 .
В результате, закон распределения числа очков, выбиваемых командой, если стрелки сделают по одному выстрелу, имеет вид:
|
Y |
|
5 |
|
6 |
7 |
|
8 |
|
|
9 |
|
|
|
10 |
|
P |
|
0,06 |
|
0,11 |
0,16 |
|
0,26 |
|
0,26 |
|
|
|
0,15 |
|
2) Определим дисперсии: |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
∑P(Y = yi |
|
|
2 |
|
||
D( X1 + X 2 ) = D(Y ) = M (Y 2 ) − M (Y )2 = ∑P(Y = yi ) yi2 − |
) yi . |
|
|||||||||||||
|
|
|
|
|
|
i |
|
i |
|
|
|
|
|
||
∑P(Y = yi ) yi2 |
= 0,06 52 |
+ 0,11 62 + 0,16 72 + 0,26 82 |
+ 0,26 92 |
+ 0,15 102 |
= 66 . |
||||||||||
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑P(Y = yi ) yi |
= 0,06 5 + 0,11 6 + 0,16 7 + 0,26 8 + 0,26 9 + 0,15 10 = 8 . |
|
|
||||||||||||
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D( X1 + X 2 ) = 66 −82 = 2 .
|
|
∑P( X1 |
|
2 |
D(X1 ) = M (X12 ) − M ( X1 )2 = ∑P(X1 = x1i )x12i − |
= x1i )x1i . |
|||
i |
|
i |
|
|
∑P(X1 = x1i )x12i = 0,3 32 + 0,4 42 + 0,3 52 |
=16,6 . |
|
|
|
i |
|
|
|
|
∑P(X1 = x1i )x1i = 0,3 3 + 0,4 4 + 0,3 5 = 4 .
i
D(
D(
∑
i
X1 ) =16,6 − 42 |
= 0,6 . |
|
|
|
|
|
|
|
X 2 ) = M ( X 22 ) − M (X 2 )2 = ∑P(X 2 |
= x2i )x22i − |
|
∑P( X 2 |
|
2 |
|||
|
= x2i )x2i . |
|||||||
|
i |
|
|
|
i |
|
|
|
P(X 2 = x2i )x22i |
= 0,2 22 + 0,1 32 |
+ 0,2 42 + 0,5 52 |
=17,4 . |
|
||||
∑P(X 2 = x2i )x2i |
= 0,2 2 + 0,1 3 + 0,2 4 + 0,5 5 = 4 . |
i |
|
D(X 2 ) =17,4 − 42 |
=1,4 . |
Действительно, |
|
D( X1 ) + D(X 2 ) = 0,6 +1,4 = 2 = D(X1 + X 2 ) ,
т.е. равенство верно.
Задача 84. Случайная величина X задана плотностью вероятности
0, |
x ≤ 0, |
f (x) = a sin x, |
0 < x ≤ π, |
0, |
x > π. |
Найти: |
|
1)значение параметра a;
2)функцию распределения F(x);
3)вероятность попадания случайной величины X в интервал − π, π ;
4 4
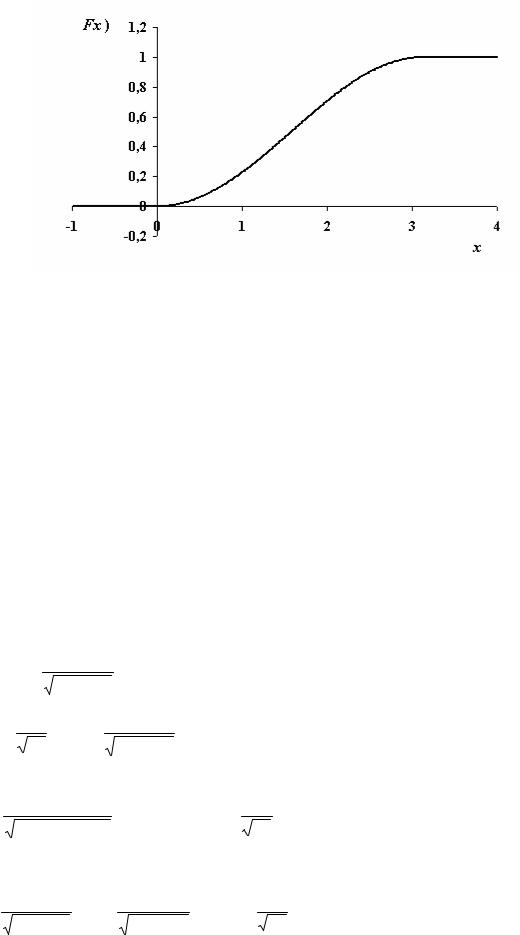
4)построить графики f(x), F(x).
Решение.
1) Воспользуемся условием нормировки: +∞∫ f (x)dx =1 .
−∞
Следовательно,
0 π +∞
∫0dx + ∫a sin xdx + ∫0dx =1,
−∞ 0 π
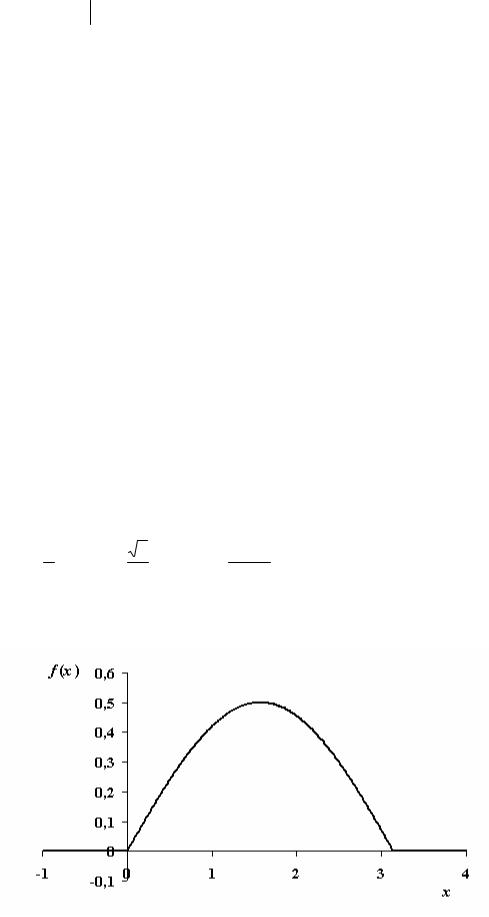
откуда
π
a ∫sin xdx = − a cos x 0π = −a(−1 −1) = 2a =1.
0
Таким образом, a = 0,5 . Итак,
0, |
x ≤ 0, |
|
0 < x ≤ π, |
f (x) = 0,5sin x, |
|
|
x > π. |
0, |
2) Функция распределения F(x) = ∫х f (x)dx .
−∞
Для x ≤ 0 F(x) = 0, т.к. при x ≤ 0 f(x) = 0.
Для 0 < x ≤ π
x |
0 |
x |
F(x) = ∫ |
f (x)dx = ∫0 dx + 0,5∫sin xdx = −0,5cos x |
|
−∞ |
−∞ |
0 |
Поскольку при x > π f(x) = 0, то, очевидно, что для всех
x
0
=−0,5(cos x −1) = 0,5 − 0,5cos x .
x> π F(x) = F (π) = −cos π =1. Итак,
|
|
0, |
|
|
|
x ≤ 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− 0,5cos x, 0 < x ≤ π, |
|
|
|
|
|
|
|
|
|
|
|
|||||
F(x) = 0,5 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
x > π. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3) Т.к. по определению F(x) = P(X < x) |
и P(X < x) + P(X ≥ x) =1, то |
|
|
||||||||||||||||
|
π |
< X |
< |
π |
|
|
π |
|
π |
|
|
π |
|
− |
π |
= −cos |
π |
−0 |
= |
P − |
4 |
4 |
|
= P X < |
|
− P X < − |
|
= F |
− F |
|
|
4 |
|||||||
|
|
|
|
|
4 |
|
4 |
|
|
4 |
|
|
4 |
|
|
|
|||
= 0,5 −0,5cos |
π |
= 0,5 −0,5 |
2 |
= 0,5 − 0,5 |
1,4142 |
= 0,1464 . |
|
|
|
|
|
|
|||||||
|
|
|
|
4 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
4) Графики f(x), F(x) имеют вид:
Задача 85. Вероятность найти белый гриб среди прочих равна ¼. Какова вероятность того, что: а) среди 300 грибов белых будет 75; б) белых грибов будет не менее 50 и не более 100?
Решение.
Поскольку количество грибов n – велико, то используем вместо биномиального распределения его аппроксимацию. В данном случае p = 0,25. При этом: np = 300 0,25 = 75 >10 , np(1− p) = 300 0,25 0,75 = 56,25 > 20 , поэтому используем нормальную
аппроксимацию.
а) Если вероятность p наступления события A в каждом испытании постоянна и отлична от
0 и 1, то вероятность Pn, p (k) того, что событие A произойдет k раз в достаточно большом числе
n независимых испытаниях приближенно вычисляется по формуле
|
Pn, p (k) ≈ |
|
f (t) |
|
|
, |
|
|
|
|
|
|
|
|
||
|
np(1− p) |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где |
f (t) = |
1 |
e− |
t2 |
, t = |
|
k −np . |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
2π |
|
|
|
|
|
np(1− p) |
|
|
|
|
|
|
|
|
|
Отсюда получим |
|
|
|
|
|
|
|
|
|
|
|||||
|
t = |
75 −300 0,25 |
|
= 0 , f (t) = f (0) = 1 |
|
e0 |
= 0,39894 , P |
(75) = 0,0532 . |
||||||||
|
|
300 0,25 0,75 |
|
|
2π |
|
|
300;0,25 |
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||
|
б) Применяем формулу Pn, p (c ≤ vn ≤ d )→ F0 (t2 ) − F0 (t1 ) , |
|
||||||||||||||
|
|
c −np |
|
|
|
d −np |
|
|
1 |
t |
x2 |
|
||||
где |
t = |
; t |
|
= |
; |
F (t) = |
e− |
|
dx − кривая Гаусса, значения которой |
|||||||
2 |
2 |
|||||||||||||||
|
1 |
np(1− p) |
|
|
np(1− p) |
|
0 |
2π −∫∞ |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
определяются из таблиц. Имеем

t = 50 −75 |
= −3,33333, t |
2 |
= 100 −75 |
=3,33333, |
|||
1 |
75 |
0,75 |
|
75 |
0,75 |
|
|
|
|
|
|
||||
F0 (t2 ) − F0 (t1 ) = F0 (3,33333) − F0 (−3,33333) = 0,99957 −0,00043 = 0,99914 . Таким образом, P300;0,25 (50 ≤ k ≤100)≈ 0,99914 .
Задача 86. Обзор счетов 400 инвесторов на фондовой бирже дал следующую информацию о числе сделок в течение последнего квартала:
Число сделок, X |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
Число держателей |
|
|
|
|
|
|
|
|
|
|
|
финансовых |
146 |
97 |
73 |
34 |
23 |
10 |
6 |
3 |
4 |
2 |
2 |
инструментов |
|
|
|
|
|
|
|
|
|
|
|
1.Постройте график распределения X.
2.Найдите вероятность того, что случайно выбранный инвестор произвел ноль сделок; по крайней мере, одну сделку; больше пяти; меньше шести.
3.Найдите математическое ожидание и дисперсию числа сделок.
Решение.
1. Составим ряд распределения X. Вероятность того, что случайно выбранный инвестор произвел ноль i сделок, равна
p |
i |
= P( X = i) = |
ni |
|
= |
ni |
. |
|
|
|
|
|
|
|
|
|||
10 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
∑ni |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
i=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда ряд распределения X. примет вид, показанный в таблице: |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Число |
0 |
|
1 |
|
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||||
сделок, X |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
pi |
|
0,365 |
|
0,2425 |
|
0,1825 |
0,085 |
0,0575 |
0,025 |
0,015 |
0,0075 |
0,01 |
0,005 |
0,005 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
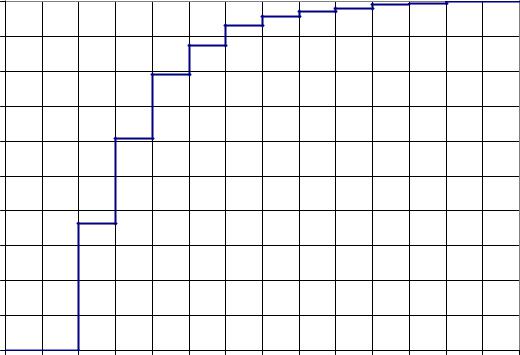
График распределения X показан на рис. 1.
F(x)
1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 11 12 |
x
Рис. 1. График распределения X.
2. Вероятность того, что случайно выбранный инвестор произвел ноль сделок, равна
P(X = 0) = |
n0 |
= |
|
n0 |
= |
146 |
= 0,365 . |
|
|
||
10 |
n |
|
|
|
|||||||
|
|
|
|
400 |
|
|
|
|
|||
|
|
∑ni |
|
|
|
|
|
|
|||
|
|
i=0 |
|
|
|
|
|
|
|
|
|
Вероятность того, что случайно выбранный инвестор произвел, по крайней мере, одну |
|||||||||||
сделку, равна |
|
|
|
|
|
|
|
|
|
|
|
P(X > 0) =1 − P( X = 0) =1 −0,365 = 0,635 . |
|||||||||||
Вероятность того, что случайно выбранный инвестор произвел больше пяти сделок, равна |
|||||||||||
|
|
10 |
|
|
|
|
|
|
|
|
|
P(X > 5) = |
|
∑ni |
|
|
6 +3 + 4 + 2 + 2 |
|
17 |
|
|||
|
i=6 |
= |
|
= |
= 0,0425 . |
||||||
|
10 |
|
|
400 |
400 |
||||||
|
|
∑ni |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
i=0
Вероятность того, что случайно выбранный инвестор произвел меньше шести сделок, равна
P(X < 6) =1 − P( X > 5) =1 −0,0425 = 0,9575 .
3. Математическое ожидание числа сделок равно

10
μX = ∑pi X i = 0,365 0 + 0,2425 1 +K+ 0,005 10 =1,535 .
i=0
Дисперсия числа сделок равна
10
σ2X = μX 2 −(μX )2 = ∑pi X i2 −(μX )2 =
i=0
= 0,365 02 + 0,2425 12 +K+ 0,005 102 −1,5352 = 3,379 .
Задача 87. Распределение вероятностей двумерной случайной величины (Х,У) задано таблицей. Найти законы распределения составляющих величин X, Y и коэффициент корреляции rxy. В случае |rxy | > 0,5 записать уравнение регрессии Y на X.
|
X |
0,1 |
0,2 |
0,3 |
Y |
|
|||
|
|
|
|
|
|
|
|
|
|
6,7 |
|
0,15 |
0,1 |
0,02 |
14 |
|
0,06 |
0,25 |
0,08 |
26 |
|
0,01 |
0,03 |
0,3 |
Решение.
Случайная величина X может принимать значения:
X = 0,1 с вероятностью p1 = 0,15 + 0,06 + 0,01 = 0,22; X = 0,2 с вероятностью p1 = 0,1 + 0,25 + 0,03 = 0,38; X = 0,3 с вероятностью p1 = 0,02 + 0,08 + 0,3 = 0,4.
Отсюда ее закон распределения имеет вид:
xi |
0,1 |
0,2 |
0,3 |
pi |
0,22 |
0,38 |
0,4 |
Аналогично, случайная величина Y может принимать значения:
Y = 6,7 с вероятностью p1 = 0,15 + 0,1 + 0,02 = 0,27; Y = 14 с вероятностью p1 = 0,06 + 0,25 + 0,08 = 0,39; Y = 26 с вероятностью p1 = 0,01 + 0,03 + 0,3 = 0,34.
Отсюда ее закон распределения имеет вид:
yj |
6,7 |
14 |
26 |
pj |
0,27 |
0,39 |
0,34 |
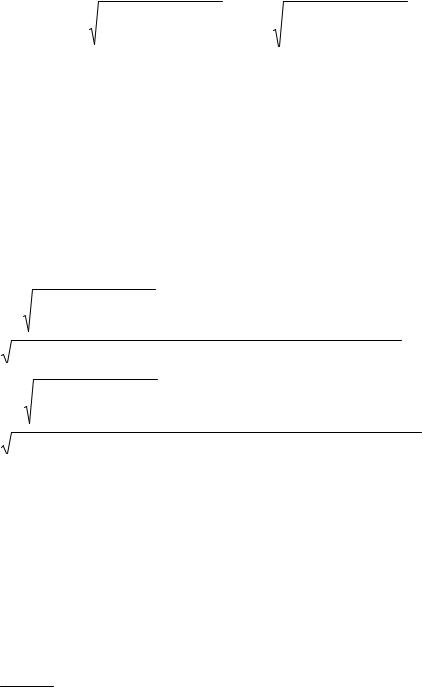
Коэффициент корреляции rxy определяется по формуле |
|
|||||||||||
r |
= |
Kxy |
|
, |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||
xy |
σ |
x |
σ |
y |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
3 |
3 |
3 |
3 |
|
где K xy |
= M ( XY ) − M (X )M (Y ) = ∑∑xi y j pij |
− ∑xi pi |
− ∑y j p j |
− ковариация случайных |
||||||||
|
|
|
|
|
|
|
|
i=1 j=1 |
i=1 |
j=1 |
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
|
величин X и Y; |
σx |
= |
∑(xi − M ( X ))2 pi , σy |
= ∑(y j − M (Y ))2 p j |
− средние квадратические |
|||||||
|
|
|
|
|
|
|
|
i=1 |
|
j=1 |
|
|
отклонения случайных величин X и Y, соответственно. Определим все эти величины: |
||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
M ( X ) = ∑xi pi |
= 0,1 0,22 +0,2 0,38 +0,3 0,4 = 0,218 ; |
|
||||||||||
|
|
|
|
i=1 |
|
|
|
|
|
|
||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
M (Y ) = ∑y j p j |
= 6,7 0,27 +14 0,39 + 26 0,34 =16,109 ; |
|
||||||||||
|
|
|
|
j=1 |
|
|
|
|
|
|
||
|
|
|
|
|
3 |
3 |
|
|
|
|
|
|
M ( XY ) = ∑∑xi y j pij = 0,1 6,7 0,15 +0,1 14 0,06 +K+0,3 26 0,3 = 3,9167 ; |
||||||||||||
|
|
|
|
|
i=1 j=1 |
|
|
|
|
|
||
Kxy = M ( XY ) − M ( X )M (Y ) = 3,917 −0,218 16,109 = 0,4049 ; |
|
|||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
σ x = ∑(xi − M ( X ))2 pi = |
|
|
|
|
||||||||
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
= |
(0,1 −0,218)2 0,22 +(0,2 −0,218)2 0,38 +(0,3 −0,218)2 0,4 = 0,0767; |
|||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
σ y = ∑(yi − M (Y ))2 pJ = |
|
|
|
|
||||||||
j=1
=(6,7 −16,109)2 0,27 +(14 −16,109)2 0,39 +(26 −16,109)2 0,34 = 7,6747;
|
rxy = |
0,4049 |
= 0,688 . |
|||
|
|
0,0767 7,6747 |
||||
|
|
|
|
|
|
|
Построим уравнение регрессии Y на X. Оно имеет вид: |
||||||
|
yx = a +bx , |
|
||||
где b = |
|
Kxy |
|
, a = M (Y ) −bM ( X ) . |
||
|
σ 2 |
|||||
|
|
|
|
|
||
|
|
x |
|
|
|
|
Подставив найденные выше значения параметров, получим
= 0,4049 b 0,07672
Таким образом, построили уравнение регрессии Y на X yx =1,086 +68,914x .

Задача 88. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины X соответственно равны 30 и 4. Найти вероятность того, что X в пяти испытаниях три раза примет значение, заключенное в интервале (29, 31).
Решение.
Определим вначале вероятность того, что X в одном испытании примет значение, заключенное в интервале (29, 31). Она определяется по формуле:
p = P( |
|
X −30 |
|
1 |
|
= 0,3829 , |
|
|
<1)= 2Φ |
4 |
= 2Φ(0,5) = 2 0,1915 |
||||
где Φ(x) |
|
|
|
|
|
|
|
– функция Лапласа, задаваемая таблично. |
|
||||||
Далее воспользуемся схемой Бернулли. Исковая вероятность будет равна |
|||||||
P (k = 3) = C 3 p3 (1− p) 2 |
=10 0,38293 (1−0,3829) 2 = 0,214 . |
||||||
5 |
5 |
|
|
|
|||
Таким образом, вероятность того, что X в пяти испытаниях три раза примет значение, заключенное в интервале (29, 31), равна 0,214.
Задача 89. Предприниматель может получить кредиты в банках: в первом – L млн. руб. с
вероятностью m1 , во втором – k млн. руб. вероятностью m1+1 , в третьем – r млн. руб. с
вероятностью m1+ 2 . Составить ряд распределения случайной величины Х – возможной суммы
кредитов и найти ее числовые характеристики, если банки работают независимо друг от друга. Значения L, k, r, m равны: L = 20 , k = 5 , r =15 , m = 4 .
Решение.
Предприниматель может получить следующие суммы (в млн. руб.): x1 = 0 ; x2 = 5 ; x3 =15 ; x4 = 20 ; x5 = 25 ; x6 = 35 ; x7 = 40 .
Обозначим события: A1 – 1-й банк выдал кредит; A2 – 2-й банк выдал кредит; A3 – 3-й банк выдал кредит. Отсюда имеем:
P(x1 ) = P( X = 0) = P( A1 )P(A2 )P( A3 ) = 34 54 56 = 63 = 12 ; P(x2 ) = P( X = 5) = P(A1 )P( A2 )P(A3 ) = 34 15 56 = 243 = 18 ; P(x3 ) = P( X =15) = P( A1 )P(A2 )P( A3 ) = 34 54 16 = 303 = 101 ;
P(x4 ) = P(X = 20) = P(A1 )P( A2 )P( A3 ) + P(A1 )P( A2 )P(A3 ) = ;
