
- •Ю. Н. Полшков
- •СОДЕРЖАНИЕ
- •Бюффон
- •Табл. 1. Выборка к примеру 3
- •Табл. 2. Упорядоченная выборка
- •Табл. 3. Таблица распределения частот
- •Табл. 4. Таблица распределения частостей
- •Табл. 5. Таблица накопленных частостей
- •Табл. 7. Таблица накопленных частот и частостей
- •Табл. 1. Таблица распределения частот к примеру 1
- •Табл. 1. Статистические данные к примеру 1
- •Табл. 2. Расчётная таблица к примеру 1
- •Табл. 3. Данные опыта Резерфорда, Чедвика и Эллиса
- •Критические точки распределения
- •Критические точки распределения Стьюдента
- •Критические точки распределения Кочрена

53
Лекция 3. МЕТОДЫU ТОЧЕЧНЫХ ОЦЕНОК ПАРАМЕТРОВ СТАТИСТИЧЕСКИХ РАСПРЕДЕЛЕНИЙ U
План
1.Метод моментов.
2.Метод максимального правдоподобия.
1.Метод моментов впервые предложил П.Л.Чебышев. Развитием этого метода занимались ученики Чебышева и английский математик К.Пирсон. Кратко суть метода может быть изложена словами: для определения точечных оценок неизвестных параметров заданного распределения необходимо приравнять теоретические моменты рассматриваемого распределения к соответствующим эмпирическим моментам того же порядка.
ПримерU 1.U Страховая компания провела анализ дневных суммарных выплат по однотипным медицинским договорам страхования. Результаты анализа (в тыс. грн.) за 100 рабочих дней сведены в табл. 1:
Табл. 1. Статистические данные к примеру 1
|
№ интервала |
1 |
2 |
3 |
|
|
4 |
|
5 |
6 |
7 |
8 |
|
|
|
Границы |
0 – 1 |
1 – 2 |
2 – 3 |
|
3 – 4 |
|
4 – 5 |
5 – 6 |
6 – 7 |
7 – 8 |
Σ |
||
|
Середина интервала |
0,5 |
1,5 |
2,5 |
|
|
3,5 |
|
4,5 |
5,5 |
6,5 |
7,5 |
||
|
Частота |
1 |
5 |
14 |
|
|
26 |
|
24 |
18 |
10 |
2 |
100 |
|
|
Частость |
0,01 |
0,05 |
0,14 |
|
|
0,26 |
|
0,24 |
0,18 |
0,10 |
0,02 |
100/100=1 |
|
Предполагая, что дневные суммарные выплаты распределены по нормальному закону |
||||||||||||||
|
|
|
|
|
1 |
|
e− |
1 (x−a )2 |
|
|
|
|
||
|
|
|
f (x) = |
|
2 |
σ 2 , |
|
|
|
|
||||
|
|
|
|
|
2πσ |
|
|
|
|
|
|
|
||
оценить методом моментов параметры а и σ .
Решение. Вычислим среднее значение выборки, причем за представителя каждого интервала (разряда) примем его середину:
x= ∑xi wi =
i=1
=0,5 0,01+1,5 0,05 + 2,5 0,14 +3,5 0,26 + 4,5 0,24 +5,5 0,18 +6,5 0,10 +7,5 0,02 = 4,21 .k
Выборочные дисперсия и стандартное отклонение, соответственно, равны:
sX |
2 = 2,1059; sX ≈1,4512 . |
Согласно методу моментов, нужно приравнять теоретические моменты рассматриваемого распределения к соответствующим эмпирическим моментам того же порядка. Следовательно, выберем параметры а и σ нормального закона так, чтобы выполнялись условия:
a = x,σ 2 = sX 2 a = 4,21;σ =1,4512 .
Подставляя оценки параметров, полученные методом моментов, в теоретическую плотность распределения, имеем
|
|
|
|
|
|
1 |
− |
1 (x−4,21)2 |
. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||
|
|
|
|
|
f (x) = |
e |
2 1,4512 |
|
|
|
|
||||
|
|
|
|
|
2π1,4512 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислим значения |
f (x) в середине каждого из интервалов: |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
Табл. 2. Расчётная таблица к примеру 1 |
||||||
|
x |
0,5 |
|
1,5 |
2,5 |
3,5 |
|
4,5 |
|
|
5,5 |
6,5 |
7,5 |
|
|
|
f (x) |
0,0105 |
|
0,0481 |
0,1373 |
0,2439 |
|
0,2694 |
|
0,1852 |
0,0792 |
0,0210 |
|
||
|
Частость |
0,01 |
|
0,05 |
0,14 |
0,26 |
|
0,24 |
|
0,18 |
0,10 |
0,02 |
|
||

54
Как видно из табл. 2, значения плотности распределения в серединах интервалов мало отличаются от частости. Построим на рис. 1 гистограмму и, по вычисленным значениям, кривую плотности.
Рис. 1. Гистограмма частостей и кривая теоретической плотности распределения.
Судя по рис. 1, что теоретическая кривая плотности распределения f (x) , в основном,
сохраняет особенности статистического распределения. Пример 1 выполнен.
ЗамечаниеU 2.U Оценки, полученные методом моментов, обычно имеют сравнительную эффективность e(θ ) существенно меньше единицы и даже являются смещёнными. Иногда,
из-за простоты их нахождения, они используются в качестве начального приближения для нахождения более эффективных оценок.
2. Наиболее распространенным методом точечных оценок параметров является метод максимального правдоподобия. Этот метод впервые был предложен Р.Фишером.
Пусть по-прежнему имеется выборка x1 , x2 ,..., xn из генеральной совокупности с неизвестной теоретической функцией распределения FX (x) , принадлежащей известному однопараметрическому семейству FX (x;θ) . Функция неизвестного параметра θ
L(x1 , x2 ,..., xn ;θ) = f (x1;θ) f (x2 ;θ)... f (xn ;θ)
называется функцией правдоподобия. Здесь f (x,θ) – плотность распределения случайной ве-
личины X при непрерывном распределении, а в случае дискретного распределения f (x,θ) = P{X = x;θ}. Замечательное свойство функций правдоподобия заключается в том,
что они как бы вбирают в себя всю информацию, которая даётся выборкой относительно параметра θ . Функция правдоподобия по сути не что иное, как вероятность (в непрерывном случае плотность распределения) получить именно ту выборку x1 , x2 ,..., xn , которую бы мы
реально имели, если бы значение неизвестного параметра равнялось θ . Естественно поэтому в качестве оценки неизвестного параметра θ выбрать θ* , доставляющее наибольшее значе-
ние функции правдоподобия L(x1 , x2 ,..., xn ;θ) . Оценкой максимального правдоподобия назы-
вается такое значение θ* , для которого
L(x1 , x2 ,..., xn ;θ* ) = max L(x1 , x2 ,..., xn ;θ) .
θ
На практике используют не саму функцию правдоподобия, а ее логарифм ln L(x1 , x2 ,..., xn ;θ) . Используя необходимое и достаточное условие экстремума функции, оценка макси-
мального правдоподобия θ* может быть найдена следующими действиями:

55
1.Найти производную ∂∂θ ln L(x1 , x2 ,..., xn ;θ) , приравнять ее к нулю и найти корень уравне-
ния правдоподобия
|
|
|
∂ |
|
ln L(x , x |
|
,..., x |
|
;θ) = 0 . |
|
|
|
|
|
2 |
n |
|||||
|
|
|
∂θ |
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
||
2. |
Найти вторую производную |
∂2 |
|
|
ln L(x , x |
|
,..., x |
|
;θ) и, если при θ =θ* вторая производ- |
|
|
|
|
|
2 |
n |
|||||
|
|
|
|
|||||||
|
|
∂θ |
2 |
1 |
|
|
||||
|
|
|
|
|
|
|
|
|||
ная отрицательна, то θ* – оценка максимального правдоподобия неизвестного параметра
θ .
ЗамечаниеU 3.U Для использования метода максимального правдоподобия необходимо,
чтобы функция правдоподобия была дифференцируемой. Оценку θ* следует искать среди значений θ , удовлетворяющих уравнению правдоподобия или принадлежащих границе области допустимых значений θ . Для наиболее важных, с практической точки зрения, се-
мейств FX (x;θ) уравнение правдоподобия имеет единственное решение θ* . Это решение и
является оценкой максимального правдоподобия.
ЗамечаниеU 4.U Метод максимального правдоподобия до настоящего момента был изложен для случая оценки одного параметра θ . Естественно, что все вышесказанное распространяется и на случай оценки k неизвестных параметров θ1 ,θ2 ,...,θk .
Перечислим достоинства метода максимального правдоподобия:
•для случая оценки одного параметра оценка максимального правдоподобия θ* всегда будет состоятельной;
•при больших объемах выборки n распределение оценки максимального правдоподобия
θ* можно приближённо считать нормальным со средним θ и дисперсией nI1(θ) , где
I (θ) – информация Фишера. Оценка θ* будет асимптотически эффективной в том
смысле, что не существует другой асимптотически нормальной оценки, имеющей меньшую дисперсию;
•если существует эффективная оценка неизвестного параметра θ E , то она является оценкой максимального правдоподобия θ* .
ПримерU 2.U Найти методом максимального правдоподобия оценку параметра λ распределения Пуассона
|
|
|
|
|
|
|
|
|
|
P( X = x) = |
λx |
e−λ , |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
x! |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пользуясь выборкой, которая дала значения x1 , x2 ,..., xn для величины X . |
|
|||||||||||||||||||||||||
Решение. Функция правдоподобия в этом случае имеет вид |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
;λ) = λx1 |
e−λ λx2 e−λ |
... λxn |
|
|
|
|
|
λx1 +x2 +...+xn |
|
|
|
∑xi |
|
||||||||
L(x |
, x |
|
,..., x |
|
e−λ = |
|
|
e−nλ = |
|
λi =1 |
e−nλ . |
|||||||||||||||
2 |
n |
|
|
|
|
|
|
|
||||||||||||||||||
1 |
|
|
|
|
x1! |
x2! |
|
xn! |
|
|
|
|
x1!x2 !...xn ! |
|
|
x1!x2 !...xn ! |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
Ее логарифм, будет таким: ln L(x1 , x2 ,..., xn ;λ) = ∑xi ln λ −ln(x1!x2 !...xn!) −nλ . |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
||
Для определения λ выпишем уравнение правдоподобия: |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ |
|
|
|
|
|
|
|
∑xi |
|
|
|
|
|
|||||||
|
|
|
|
|
|
ln L(x , x |
2 |
,..., x |
n |
;λ) = |
i=1 |
|
|
−n = |
nx |
−n = 0 . |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
∂λ |
1 |
|
|
|
|
λ |
|
|
|
λ |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
56 |
|
|
|
|
|
|
|
* |
nx |
= x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Откуда |
имеем: |
|
λ = |
|
Найдем |
теперь вторую |
производную по |
λ : |
||||||||||||||||||
|
n |
|
||||||||||||||||||||||||
|
∂2 |
ln L(x |
, x |
2 |
,..., x |
n |
;λ) = − |
nx |
. Учитывая, что значениями выборки x , x |
2 |
,..., x |
n |
могут быть то- |
|||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
∂λ2 |
1 |
|
|
|
λ2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
лько целые неотрицательные значения k = 0,1,2,... , убеждаемся в том, |
что при λ = x вторая |
|||||||||||||||||||||||||
производная отрицательна: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
∂2 |
|
ln L(x |
, x |
2 |
,..., x |
|
;λ = x) = − |
nx |
= − |
n |
< 0 . |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
∂λ2 |
1 |
|
|
n |
x 2 |
|
x |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Следовательно, оценкой максимального правдоподобия λ* |
параметра λ для распре- |
|||||||||||||||||||||||
деления Пуассона будет средняя арифметическая x . Задача решена. |
|
|
|
|
|
|||||||||||||||||||||
Хорошей иллюстрацией примера 2 может служить знаменитый опыт Резерфорда, Чедвика и Эллиса. Радиоактивное вещество наблюдали в течение N = 2608 промежутков времени, каждый длиной в 7,5 секунд, и для каждого интервала регистрировали число частиц, достигших счётчика. Всего таких частиц было зарегистрировано n =10094 . В табл. 3 приведены во втором столбце результаты этих наблюдений, в третьем столбце – отвечающие им частости, а в четвёртом – теоретические вероятности, подсчитанные по формуле Пуассона. Причем в качестве параметра λ была взята, по сути, оценка метода максимального прав-
доподобия, |
т.е. среднее число частиц x за промежуток времени t = 7,5 секунд: |
||
* |
|
10094 |
|
λ |
= |
2608 |
= 3,870 . |
Результаты выглядят довольно впечатляюще. Частости, полученные опытным путем, незначительно отличаются от теоретических вероятностей. Этот факт говорит о том, что, вопервых, был верно предугадан тип теоретического распределения (т.е. распределения Пуассона), и, во-вторых, параметр λ теоретического распределения был удачно оценен по значениям статистической выборки.
Табл. 3. Данные опыта Резерфорда, Чедвика и Эллиса
Число частиц k , |
Число наблюдений Nk , |
Частость данно- |
Теоретическая веро- |
|||||
достигших счет- |
в которых регистриро- |
го числа частиц |
ятность |
|
|
|||
чика |
валось k частиц |
W ( X = k) = |
Nk |
P( X = k) = |
3,87 |
e |
−3,87 |
|
|
|
N |
|
k! |
|
|||
|
|
|
|
|
|
|
|
|
0 |
57 |
0,022 |
|
|
0,021 |
|
|
|
1 |
203 |
0,078 |
|
|
0,081 |
|
|
|
2 |
383 |
0,147 |
|
|
0,156 |
|
|
|
3 |
525 |
0,201 |
|
|
0,201 |
|
|
|
4 |
532 |
0,204 |
|
|
0,195 |
|
|
|
5 |
408 |
0,156 |
|
|
0,151 |
|
|
|
6 |
273 |
0,105 |
|
|
0,097 |
|
|
|
7 |
139 |
0,053 |
|
|
0,054 |
|
|
|
8 |
45 |
0,017 |
|
|
0,026 |
|
|
|
9 |
27 |
0,010 |
|
|
0,011 |
|
|
|
k ≥10 |
16 |
0,006 |
|
|
0,007 |
|
|
|
Итого |
N = 2608 |
0,999 |
|
|
1,000 |
|
|
|
ЗамечаниеU 5.U В общем случае оценка максимального правдоподобия может быть не только неэффективной, но и смещённой. Однако эта смещенность не имеет существенного значения и может быть исправлена, например, домножением на соотвествующий множитель (см. предыдущую лекцию). Недостаток метода максимального правдоподобия состоит в том, что он подчас требует сложных вычислений.

57
Лекция 4. ОЦЕНКИU ПАРАМЕТРОВ С ПОМОЩЬЮ ДОВЕРИТЕЛЬНЫХ ИНТЕРВАЛОВ U
План
1.Понятие доверительного интервала.
2.Нахождение доверительного интервала для оценки математического ожидания
нормального распределения при известной дисперсии.
3.Нахождение доверительного интервала для оценки математического ожидания
нормального распределения при неизвестной дисперсии. Оценка истинного значения измеряемой величины.
4.Нахождение доверительного интервала для оценки среднеквадратического от-
клонения нормального распределения. Оценка точности измерений.
1.Оценки неизвестных параметров, полученные ранее, мы называли точечными, т.к. они оценивали параметр одним числом или точкой. Однако, точечная оценка не совпадает с оцениваемым параметром. Было бы разумно указывать те допустимые границы, в которых
может находиться неизвестный параметр θ при наблюдении выборки x1 , x2 ,..., xn . Причем,
находить эти границы надо с некоторой наперёд заданной степенью доверия или доверительной вероятностью.
Пусть оценка θ , построенная по выборке объема n , служит оценкой неизвестному параметру θ . Ясно, что чем точнее оценка θ , тем меньше абсолютная величина разности θ −θ . Если же рассматривать неравенство θ −θ <δ , то чем меньше положительное число
δ , тем оценка точнее. Таким образом, δ называют точностью оценки. Надежностью (до-
верительной вероятностью) оценки θ неизвестного параметра θ называется вероятность γ , с которой выполняется это неравенство, т.е.
P{θ −θ <δ}=γ .
В качестве надежности берут число близкое к единице: 0,95; 0,99; 0,999 и т.д. Другими словами, доверительной вероятностью можно назвать такую вероятность γ , что событие веро-
ятности 1−γ можно считать практически невозможным. Каждый конкретный случай опре-
деляет соответствующую доверительную вероятность. Например, степень надежности пассажирского самолета должна превосходить надежность электрической лампочки.
Задавшись доверительной вероятностью γ , мы должны по выборке x1 , x2 ,..., xn определить интервал [θ′;θ′′], в котором будет находиться неизвестный параметр θ . Такой интер-
вал называют доверительным интервалом, а оценку – интервальной оценкой.
ЗамечаниеU 1.U Грубой принципиальной ошибкой было бы считать доверительную вероятность γ вероятностью того, что неизвестный параметр θ будет принадлежать довери-
тельному интервалу [θ′;θ′′]. Параметр распределения θ , вообще говоря, не случаен. Границы же доверительного интервала [θ′;θ′′] случайны, т.к. находятся по значениям выборки.
Когда говорят, что неизвестный параметр θ не может выйти за границы доверительного интервала [θ′;θ′′], констатируют только тот факт, что если при любом истинном значении θ в
результате эксперимента получена выборка x1 , x2 ,..., xn , а затем по ней построен доверительный интервал [θ′;θ′′], то этот интервал с вероятностью γ накроет значение θ .
Метод доверительных интервалов впервые предложил американский математик
Ю.Нейман. Используя точечную оценку θ неизвестного параметра θ , можно строить доверительные интервалы. На практике используют обычно два типа доверительных интервалов: симметричные и односторонние. Они находятся аналогично, поэтому ограничимся рассмотрением симметричных доверительных интервалов.

58
2. В качестве примера рассмотрим задачу нахождения доверительного интервала для оценки математического ожидания нормального распределения при известной дисперсии.
Это будет первый метод нахождения доверительного интервала в конкретном случае. Пусть имеется выборка x1 , x2 ,..., xn из генеральной совокупности случайной величины
Х , характеристики которой – математическое ожидание а и дисперсия σ 2 – неизвестны. Пусть для этих параметров получены оценки:
|
1 |
n |
|
|
1 |
n |
|
x = |
∑xi |
, s 2 |
= |
∑( xi − x )2 . |
|||
n |
n |
||||||
|
i=1 |
|
|
i=1 |
Требуется построить доверительный иетервал Iγ для математического ожидания а случай-
ной величины Х .
Как и ранее, будем считать значения выборки x1 , x2 ,..., xn независимыми одинаково распределенными случайными величинами X1 , X 2 ,..., X n . Тогда величина х представляет собой сумму независимых одинаково распределенных случайных величин Хi , и, согласно
центральной предельной теореме (см. лекцию 9), при достаточно большом n ее закон распределения близок к нормальному. Параметрами нормального распределения является математическое ожидание и дисперсия (или среднеквадратическое отклонение). Найдем их:
Таким
σ(x) =
ния
|
|
|
X |
1 |
+ X |
2 |
+... + X |
n |
|
|
|
|
1 n |
1 |
|
|
|
|
|
|
|||||||||
|
Mx = M |
|
|
|
|
|
|
|
|
= |
|
|
∑MX i = |
|
|
|
nMX = MX = a , |
|
|||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n i=1 |
|
|
|
|
|
|
|
||||||
|
|
X |
1 |
+ X |
2 |
+... + X |
n |
|
|
|
|
|
1 |
|
D( X1 + X 2 |
|
|
... + X n ) = |
nσ 2 |
|
σ 2 |
|
|||||||
|
D(x) = D |
|
|
|
|
|
|
|
|
= |
|
|
|
|
+ |
|
= |
|
|
. |
|||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
n2 |
n2 |
|
n |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
образом, параметрами |
распределения |
|
случайной |
|
величины х |
|
будут Mx = a и |
||||||||||||||||||||||
σ |
. Предположим, что величина σ нам известна. Потребуем выполнение соотноше- |
||||||||||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P{x − a <δ}=γ ,
где γ – заданная надежность. Т.к. случайная величина х |
распределена по нормальному за- |
||||||||||||||||
кону с параметрами Mx = a и σ(x) = |
σ |
, то, пользуясь свойством 2 нормального распреде- |
|||||||||||||||
ления (лекция 7), получим |
|
n |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P{ |
x −a |
|
<δ}= 2Φ |
δ |
= 2Φ δ |
n |
def= 2Φ(t) . |
||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
σ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
1 |
t |
|
|
|
|
|
|
|
tσ |
|
|
|
|
|
|
|
Здесь Ф(t) = |
∫e |
−z 2 |
/ 2 |
dz . Найдя |
δ = |
, можно написать |
|
|
|||||||||
π |
|
|
n |
|
|
||||||||||||
|
2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P x −a < tσ |
= 2Φ(t) |
|
|
|
||||
или |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P x − tσ |
< a < x + tσ |
|
= 2Φ(t) =γ . |
||||||||
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|||
Т.о., с надежностью γ |
|
доверительный интервал |
Iγ |
= x − tσ |
; x + tσ покрывает неизвест- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n |
ный параметр a , причем точность оценки δ = |
tσ . Число t |
определяется из равенства |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
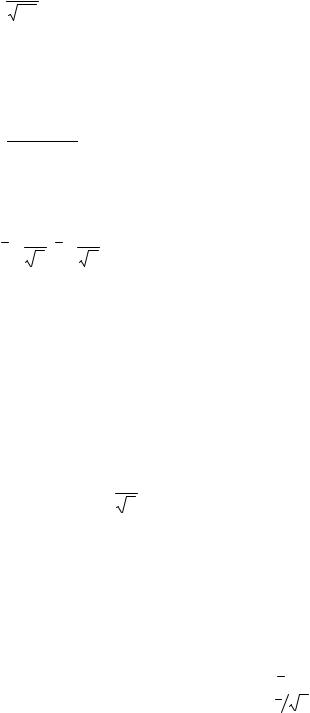
|
|
|
|
|
|
|
|
|
59 |
|
|
|
|
|
|
2Φ(t) =γ |
или Φ(t) = γ . |
|
|
|
|
|
|
|
|
|
|
2 |
|
Т.е., по таблице интегральной функции Лапласа находят аргумент t , |
при котором эта функ- |
||||||||
ция принимает значение γ |
. Если использовать статистические функции из Microsoft Excel, |
||||||||
|
|
|
|
|
2 |
|
|
|
γ +0,5 . Это связано с |
то для нахождения t |
надо вычислять НОРМСТОБР( ) от аргумента |
||||||||
|
|
|
|
|
|
|
|
|
2 |
тем, что |
в |
этом |
пакете |
используется |
функция распределения |
нормального закона |
|||
F (t) = |
1 |
∫t |
e−z 2 / 2 dz . Напомним, что с функцией Лапласа она связана соотношением |
||||||
|
2π |
−∞ |
|
|
|
F (t) = Φ(t) + 1 . |
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2 |
|
Можно использовать пакет Maple. В Maple 6, |
например, для нахождения t нужно вычислить |
||||||||
stats[statevalf,icdf,normald[0,1]]( ) от аргумента |
γ + 0.5 . |
|
|||||||
|
|
|
|
|
|
|
|
2 |
|
|
ПримерU |
1.U По данным примера 1 лекции 12, предполагая, что стандартное отклонение |
|||||||
случайной величины X равно σ =1,4512 , построить доверительный интервал для математического ожидания а с доверительной вероятностью 0,95.
|
Решение. При решении примера 1 лекции 12 была найдена выборочная средняя |
|||
x = 4,21 . |
|
Требуется найти с надежностью γ = 0,95 доверительный интервал |
||
Iγ |
|
tσ |
; x + |
tσ |
= x − |
|
, который покрывает неизвестное математическое ожидание a . Стати- |
||
|
|
n |
n |
|
стических данных в задаче 100. Однако, т.к. все параметры оценивались с использованием середин 8 интервалов, то будет правильным взять n = 8 . В нашем случае γ2 = 0,475 . Число t
определяется из равенства Φ(t) = 0,475 . Воспользовавшись таблицей значений интегральной функции Лапласа, получим t =1,96 . Если использовать статистические функции из Microsoft
Excel, то нужно вычислить НОРМСТОБР( ) от аргумента γ2 +0,5 = 0,975 , т.е.
t = НОРМСТОБР(0,975) = 1,959961.
Используя пакет Maple 6, получим
нормальному закону. Поэтому рассмотрим задачу нахождения доверительного интервала для оценки математического ожидания нормального распределения при неизвестной дис-
t = stats[statevalf, icdf, normald[0,1]](0.975) = 1.95996. |
||||
Далее рассчитываем |
tσ |
=1,00561. Т.о. доверительным интервалом для математического |
||
|
n |
|
|
|
ожидания а с надежностью 0,95 будет интервал I0,95 = (3,20439;5,21561). |
||||
|
|
T = |
x − a |
, |
|
|
|
||
|
|
|
s n |
|
персии. Случай, когда дисперсия известна, был рассмотрен выше.
n |
нахождения доверительного интервала в кон- |
3. Рассмотрим теперь второй метод |
|
кретном случае. Наиболее встречающаяся ситуация, когда величина Х распределена по |
|
По данным выборки можно построить случайную величину:
где х – выборочная средняя, s – исправленное выборочное среднеквадратическое отклоне-
ние, т.е. s 2 = |
n |
|
s 2 = |
1 |
∑(xi − x)2 , n – объем выборки. Значения, принимаемые случай- |
|
n −1 |
|
n −1 i=1 |
||
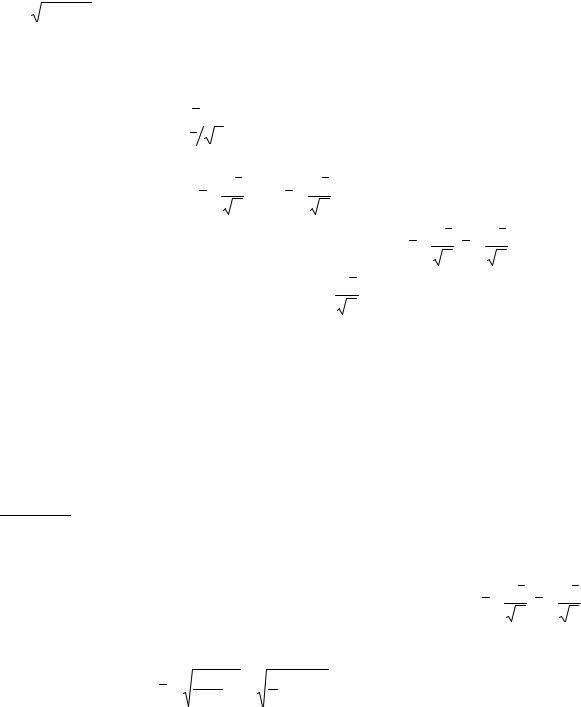
60
ной величиной T , будем обозначать через t . Случайная величина T имеет распределение Стьюдента с k = n −1 степенями свободы. Это распределение впервые ввел английский статистик В. Госсет, более известный под псевдонимом “Стьюдент”. Плотность распределения Стьюдента
S(t, n) = B |
1+ |
t 2 |
−n / 2 . |
|
|||
|
n |
|
|
|
|
n −1 |
|
|
n |
|
|
|
|
|
|
|
Γ |
|
|
|
|
|
∞ |
|
|
|
|
|
|||
Здесь Bn = |
2 |
|
|
|
|
, где Γ(x) = ∫u x−1e−u du – т.н. гамма-функция. |
|
|
|
n −1 |
|
||||
|
π(n −1)Γ |
|
|
|
0 |
||
|
2 |
|
|||||
|
|
|
|
|
|
|
|
Распределение Стьюдента определяется параметром n – объемом выборки и не зависит от неизвестных параметров a и σ . Эта особенность – несомненно большое достоинство.
Т.к. S(t, n) – четная функция от t , то |
|
|
|
|
||
|
|
x −a |
|
|
|
tγ |
|
|
|||||
|
|
|
|
|
= 2∫S(t, n)dt =γ , |
|
P |
|
|
|
|
< tγ |
|
|
s n |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|||||
или, переписав в другом виде,
|
tγ s |
< a < x + |
tγ s |
=γ . |
P x − |
n |
|
||
|
|
n |
|
|
|
|
|
|
tγ s |
|
tγ s |
|
Следовательно, с надежностью γ доверительный интервал |
Iγ |
|
|
; x + |
|
покрывает |
||
= x − |
n |
|
||||||
|
|
|
|
|
|
n |
|
|
неизвестный параметр |
a , причем точность оценки δ = tγ s |
. Число tγ |
определяется из специ- |
|||||
|
n |
|
|
|
|
|
|
|
альных таблиц. Наиболее распространённые таблицы содержат значения tγ = t(γ, n) , которые определяются по заданным n и γ . Можно использовать также таблицу критических точек распределения Стьюдента. В ней tγ будет определяться по заданному уровню значимости α =1 −γ для двусторонней критической области и по заданному числу степеней свободы k = n −1. Если использовать статистические функции из Microsoft Excel, то для нахождения tγ надо вычислять СТЬЮДРАСПОБР(1 −γ; k) . В Maple 6 для нахождения tγ нужно вычис-
лить stats[statevalf, icdf, studentst[ k ]]( ) от аргумента γ2 + 0.5 .
ПримерU 2.U По данным примера 1 лекции 12, полагая, что случайная величина Х рас-
пределена по нормальному закону и ее дисперсия неизвестна, построить доверительный интервал для математического ожидания а с доверительной вероятностью 0,95.
Решение. Оценки параметров распределения известны: x = 4,21; s2 |
= 2,1059; s =1,4512 . |
||||
|
|
tγ s |
|
tγ s |
|
Требуется найти с надежностью γ = 0,95 доверительный интервал Iγ |
|
|
; x + |
|
, |
= x − |
n |
|
|||
|
|
|
n |
|
|
который покрывает неизвестное математическое ожидание a . Т.к. объём выборки n = 8 , то исправленное выборочное среднеквадратическое отклонение равно:
s = |
n |
s 2 = |
8 |
2,1059 ≈1,5514 . |
|
n −1 |
|
7 |
|
Воспользовавшись таблицей значений tγ = t(γ, n) , определяем tγ = t(0,95;8) = 2,37 . В Micro-
soft Excel для тех же целей вычисляют
tγ = СТЬЮДРАСПОБР(0,05;7) = 2,364623.

61
При использовании пакета Maple 6 рассчитывают
tγ = stats[statevalf, icdf, studentst[7]](0.95/2+0.5)=2.36462.
Вычисляя tγ ns =1,297 , убеждаемся в том, что доверительным интервалом для математиче-
ского ожидания а с надёжностью 0,95 будет интервал I0,95 = (2,913;5,507).
ЗамечаниеU 2.U При неограниченном росте объёма выборки n распределение Стьюдента
стремится к нормальному. Практически при n > 30 можно вместо распределения Стьюдента использовать нормальное распределение.
При малых объемах выборки n < 30 доверительный интервал, найденный по интегральной функции Лапласа (т.е. первым методом) является более узким, чем интервал, найденный по распределению Стьюдента (второй метод). Это свидетельствует не о слабости метода Стьюдента, а объясняется тем, что малая выборка содержит малую информацию о признаке Х . Рассмотренные примеры 1 и 2 демонстрируют сказанное выше.
Поговорим теперь об оценке истинного значения измеряемой величины.
Пусть по n независимым измерениям одинаковой точности нужно оценить истинное значение а некоторой физической величины. Результаты отдельных измерений будем рассматривать как случайные величины X1 , X 2 ,..., X n . Эти величины независимы (т.к. измере-
ния независимы), имеют одинаковое математическое ожидание а (истинное значение изме-
ряемой величины), одинаковые дисперсии σ 2 (точность измерений одинакова) и распределение нормально (такое предположение подтверждается опытом). Т.е., все предположения, допускаемые в первом и втором методах нахождения доверительных интервалов, выполняются. Следовательно, формулы, выведенные в этих методах, применимы и в этом случае. Таким образом, истинное значение измеряемой величины можно оценивать по среднему арифметическому результатов измерений с помощью доверительных интервалов. Здесь метод Стьюдента предпочтительнее, поскольку в задачах практики значение σ обычно неизвестно.
4. Рассмотрим задачу нахождения доверительного интервала для оценки среднеквадратического отклонения нормального распределения.
Пусть некий количественный признак Х генеральной совокупности распределен нормально. Требуется оценить неизвестное генеральное среднеквадратическое отклонение σ по исправленному выборочному среднеквадратическому отклонению s . Найдем доверительные интервалы, покрывающие параметр σ с заданной надежностью γ . Следовательно,
должно выполниться соотношение
P{σ − s <δ}=γ
или
P{s −δ <σ < s +δ}=γ .
Как и ранее, следует воспользоваться известной случайной величиной, для которой имеются вычислительные таблицы или готовые статистические функции в каком-нибудь пакете прикладных программ. Чтобы прийти к такой случайной величине проделаем некоторые преобразования. Для начала запишем неравенство
в виде |
|
|
s −δ <σ < s +δ |
|
||
|
|
|
δ |
|
δ |
|
|
|
|
− |
|
||
|
|
s 1 |
|
<σ < s 1+ |
. |
|
|
δ |
|
|
s |
|
s |
Обозначив |
def |
|
|
|
|
|
s |
= q , получим |
|
|
|
|
|
|
s(1− q)<σ < s(1+ q). |
|||||
|
|
|||||
Требуется найти q . Для этого введем в рассмотрение случайную величину χ :

62
χ = s σn −1 ,
где n – объём выборки.
Случайная величина s 2 (σn2−1) распределена по т.н. закону χ2 с n −1 степенями сво-
боды. Плотность же распределения χ имеет вид
χ n−2 e−χ2 / 2
R(χ, n) = 2(n−3) / 2 Γ n −1 .
2
Как видно распределение не зависит от оцениваемого параметра σ , а зависит только от объ- |
||||||||
ёма выборки n . Рассмотрим вероятность P{χ1 |
< χ < χ2 }= γ . Следовательно |
|||||||
|
|
|
|
|
χ2 |
|
|
|
P{χ1 < χ < χ2 }= ∫R(χ, n)dχ = γ . |
||||||||
|
|
|
|
|
χ1 |
|
|
|
Перепепишем последнее неравенство для интервальной оценки σ в следующем виде: |
||||||||
1 |
|
1 |
|
|
1 |
|
||
|
|
|
< |
|
< |
|
. |
|
|
s(1 + q) |
σ |
s(1 − q) |
|||||
Естественно, предполагается, что q <1. |
Домножим члены последнего неравенства на |
|||||||
s n −1 . Имеем оценку |
|
|
|
|
|
|
||
n −1 < s n −1 < |
n −1 , |
|||||||
1 + q |
|
σ |
|
|
1 − q |
|||
откуда |
|
|
|
|
|
|
||
|
n −1 |
< χ |
< |
n −1 . |
||||
|
1 + q |
|
|
|
1 − q |
|||
В силу равносильности преобразований, получаем следующее соотношение: |
||||||||
|
|
|
|
|
|
n−1 /(1−q) |
||
P{s(1 − q)< σ < s(1 + q)}= ∫R(χ, n)dχ = γ . |
||||||||
 n−1 /(1+q)
n−1 /(1+q)
Из последнего уравнения по заданным n и γ можно найти q . Действительно, имеем
1 |
|
< |
χ |
< |
1 |
1 |
, |
1 + q |
|
n −1 |
|
− q |
|
||
1 − q < |
n −1 |
<1 + q , |
|||||
|
|
|
χ |
|
|
|
|
− q < |
n −1 −1 < q . |
|
|||||
|
|
|
χ2 |
|
|
|
|
Следовательно, зная значение χ2 , в качестве q можно взять |
|||||||
|
q = |
n −1 |
−1. |
|
|||
|
|
|
χ 2 |
|
|
|
|
Т.о. определён алгоритм нахождения доверительного интервала, покрывающего |
|||||||
оценку среднеквадратического отклонения |
нормального распределения σ с заданной на- |
||||||
дёжностью γ . Для выполнения этой задачи нужно: а) вычислить по выборке исправленное
выборочное среднеквадратическое отклонение s ; б) найти по таблице или программными |
|
средствами q ; в) выписать доверительный интервал Jγ = (s(1 − q); s(1 + q)) |
или |
Jγ = (s − sq; s + sq).

63
Число q определяется из таблицы значений q = q(γ, n) по заданным n и γ . Можно использовать также таблицу критических точек распределения χ2 . В ней χ2 будет опреде-
ляться по заданному уровню значимости α = γ и по заданному числу степеней свободы
k = n −1. Откуда q может быть определено, как q = |
k −1. Аналогичный подход приме- |
|||
|
|
|
|
χ2 |
няется, если использовать статистические функции из Microsoft Excel: |
||||
|
|
|
q =КОРЕНЬ( k /ХИ2ОБР( k ;γ ))-1. |
|
В Maple 6 число χ2 определяется как |
|
|||
|
|
|
χ2 = stats[statevalf, icdf, chisquare[ k ]](1 −γ ), |
|
откуда |
|
q = sqrt( k / χ2 )-1. |
|
|
|
|
|
|
|
|
ПримерU |
3.U По данным примера 1 лекции 12, полагая, что случайная величина Х рас- |
||
|
|
|
|
|
пределена по нормальному закону, построить доверительный интервал для среднеквадратического отклонения σ с доверительной вероятностью 0,95.
Решение. Напомним, что s =1,5514 и n = 8 – объём выборки. Требуется найти с надёжностью γ = 0,95 доверительный интервал Jγ = (s − sq; s + sq), который покрывает неизвестное среднеквадратическое отклонение σ . Число q можно определить из таблицы значений q = q(γ, n) , т.е. q = q(0,95;8) = 0,8 . Применяя Microsoft Excel, получим
q = КОРЕНЬ(7/ХИ2ОБР(7;0,95))-1 = 0,797151.
Используя Maple 6, сначала рассчитаем число
χ2 = stats[statevalf, icdf, chisquare[7]](1-0.95) = 2.167349909,
откуда
q = sqrt(7/2.167349909)-1 = 0.797151.
Вычислим sq =1,2367 . Доверительным интервалом для среднеквадратического отклонения σ с доверительной вероятностью 0,95 будет интервал J0,95 = (0,3147;2,7881).
ЗамечаниеU 3.U Ранее предполагалось, что q <1. Если же q >1 , то учитывая, что σ > 0 ,
доверительный интервал следует находить в следующем виде: 0 < σ < s(1 + q).
Причём q находится теми же способами.
Скажем несколько слов об оценке точности измерений.
В теории ошибок принято точность измерений характеризовать средним квадратическим отклонением σ случайных ошибок измерений. В качестве оценки σ используют несмещённое выборочное стандартное отклонение s . Обычно результаты измерений взаимно независимы, имеют одно и то же математическое ожидание (истинное значение измеряемой величины) и одинаковую дисперсию (в случае измерений равной точности). Поэтому методы, применяемые при нахождении доверительного интервала для оценки среднеквадратического отклонения нормального распределения, годятся и для оценки точности измерений.

64
Лекция 5. ОБЩИЕU ПОНЯТИЯ О СТАТИСТИЧЕСКИХ ГИПОТЕЗАХ И ИХ ПРОВЕРКЕ U
План
1.Статистическая гипотеза. Виды статистических гипотез. Ошибки первого и второго рода.
2.Статистический критерий проверки нулевой гипотезы. Критическая область. Область принятия гипотезы. Критические точки.
3.Нахождение критических областей. Мощность критерия.
1.Уже не раз упоминалось о том, что в задачах математической статистики важно знать закон распределения генеральной совокупности. Если же мы только приблизительно знаем, что данная генеральная совокупность распределена по конкретному закону, то по этому поводу мы можем выдвинуть гипотезу. В этой гипотезе будет идти речь о виде предполагаемого распределения. В другом случае закон распределения может быть известен, однако неизвестны его параметры. Если имеются основания предположить, что неизвестный
параметр θ равен определенному значению θ0 , то выдвигают гипотезу: θ =θ0 . Т.о., в этой
гипотезе речь идет о предполагаемой величине параметра какого-то известного распределения. В рамках математической статистики часто выдвигаются и другие гипотезы: о равенст-
ве параметров распределений, о независимости выборок и т.д.
Статистическая гипотеза – это гипотеза о типе неизвестного распределения или о параметрах известных распределений. Например, гипотезы: 1) генеральная совокупность распределена по показательному закону; 2) дисперсии двух нормальных совокупностей равны, являются статистическими. Гипотеза: «Я смогу доказать Великую теорему Ферма», не будет статистической. Выдвинутую гипотезу H0 принято называть нулевой или основной.
Противоречащую ей гипотезу H1 называют конкурирующей или альтернативной. Если гипотеза содержит ровно одно предположение, то её называют простой. К примеру, гипотеза H0 : параметр закона распределения Пуассона λ = 7 – простая. Сложной называют гипотезу,
состоящую из конечного или бесконечного числа простых гипотез. Например, сложная гипотеза H : λ > 7 состоит из бесконечного числа простых гипотез Hi : λ = bi (bi > 7) . Гипотеза
H0 : математическое ожидание нормального распределения равно 5 (параметр σ неизвестен)
– сложная. В то же время, эта гипотеза при известном параметре σ является простой. Статистическая гипотеза называется параметрической, если в ней делаются предпо-
ложения относительно области изменения неизвестного параметра (или нескольких параметров) для заданных параметрических семейств функций распределения. Примеры параметрических гипотез: 1) дисперсии двух нормальных совокупностей равны; 2) параметр закона распределения Пуассона λ = 7 ; 3) математическое ожидание нормального распределения равно 5 (параметр σ неизвестен); 4) вероятность успеха в схеме Бернулли заключена между 0,3 и 0,6 и т.д. Примерами непараметрических гипотез служат высказывания: 1) генеральная совокупность распределена по показательному закону; 2) теоретическая функция распределения генеральной совокупности является нормальной; 3) теоретическая функция распределения не является нормальной; 4) функция распределения генеральной совокупности имеет положительное математическое ожидание и т.д.
Естественно, что выдвигаемые гипотезы нуждаются в проверке. В силу того, что методы проверки – статистические, то речь идет о статистической проверке гипотез. При проверке возможны ошибки.
Ошибка первого рода состоит в том, что правильная гипотеза будет отвергнута. Ошибка второго рода состоит в том, что неправильная гипотеза будет принята. Например, если отвергнуто правильное решение «к зданию факультета можно сделать пристройку», то эта ошибка первого рода и она, по-видимому, приведёт только к материальному ущербу. Ес-

65
ли же будет принято неправильное решение «продолжать строительство», то, возможно, что здание рухнет. Т.е. кроме материального ущерба такая ошибка может привести к гибели людей. Можно привести пример, когда ошибка первого рода имеет более тяжёлые последствия, нежели ошибка второго рода.
Правильное решение тоже может быть принято в двух случаях: 1) принята гипотеза, которая является верной; 2) отвергнута гипотеза, которая и в действительности является неверной.
Вероятность совершить ошибку первого рода называют уровнем значимости и обозначают через α . В качестве уровня значимости рассматривают небольшие вероятности: 0,05; 0,01 и т.д.
2. Для проверки нулевых гипотез используют специально подобранные случайные величины, точное или приближённое распределение которых известно. Среди них: нормально распределённая случайная величина; случайная величина F , распределённая по закону Фишера-Снедекора; случайная величина T , распределенная по закону Стьюдента; случайная
величина χ2 и др. Вообще, статистическим критерием называют случайную величину K , с помощью которой проверяют нулевую гипотезу. Для проверки гипотезы по данным кон-
кретных выборок вычисляют наблюдаемое значение критерия Kн .
После того, как выбран конкретный критерий, множество всех его возможных значений разбивают на два непересекающиеся подмножества. Критической областью называют множество значений критерия, при которых нулевую гипотезу отвергают. Областью принятия гипотезы называют множество значений критерия, при которых гипотезу принимают.
Сформулируем основной принцип проверки статистических гипотез. Если наблю-
даемое значение критерия попадает в критическую область – гипотеза отвергается. Если же наблюдаемое значение критерия принадлежит области принятия гипотезы, то гипотеза принимается.
Пусть критерий K – одномерная случайная величина. Тогда все её возможные значения принадлежат некоторому интервалу. Естественно, что критическая область и область принятия гипотезы тоже будут интервалами. Следовательно, имеются точки, которые разделяют эти области. Точки, отделяющие критическую область от области принятия гипотезы, называю критическими, и обозначают kкр . Различают односторонние и двусторонние крити-
ческие области. Среди односторонних областей обычно выделяют правосторонние и левосторонние. Правосторонней называют критическую область, которая определяется неравенством K > kкр , где kкр – положительное число. В свою очередь, левосторонней называется
критическая область, определяемая неравенством K < kкр , где kкр – отрицательное число.
Двусторонней называют критическую область, которая определяется неравенствами K < k1 , K > k2 , где k2 > k1 . В частности, если критические точки симметричны относительно
нуля, то двустороннюю критическую область (при kкр > 0 ) можно определить неравенствами
K< −kкр , K > kкр , или равносильным неравенством K > kкр .
3.Изложим теперь простейшие методы нахождения критических областей. Для определенности рассмотрим правостороннюю критическую область. Для нахождения критиче-
ской точки kкр задают достаточно малый уровень значимости α . А саму критическую точку kкр определяют из условия
P{K > kкр} =α .
Для известных критериев имеются таблицы, по которым находят соответствующую критическую точку. После нахождения критической точки, по данным конкретных выборок рассчитывают наблюдаемое значение критерия Kн . Если окажется, что Kн > kкр , то нулевую гипо-

66
тезу отвергают. В противном же случае говорят, что нет оснований отвергнуть нулевую гипотезу.
ЗамечаниеU 1.U Наблюдаемое значение критерия Kн может оказаться больше, чем kкр
не только лишь потому, что нулевая гипотеза ложна. Среди других причин следующие: малый объём выборки, условия эксперимента имеют недостатки, неудачно выбран статистический критерий и т.д. Т.о. нулевая гипотеза может быть и правильной. Отвергая её, мы с вероятностью α совершаем ошибку первого рода. В книгах по контролю качества продукции вероятность признать негодной партию годных изделий называют «риском производителя», а вероятность принять негодную партию – «риском потребителя».
ЗамечаниеU 2.U Ошибочно думать о том, что если нулевая гипотеза принята, то тем самым она доказана. Частный пример, подтвердивший справедливость общего утверждения, ещё не доказывает его. Поэтому говорить о принятии нулевой гипотезы нужно достаточно сдержанно. Слова могут быть такими: «данные наблюдений согласуются с нулевой гипотезой и не дают оснований её отвергать». На практике для большей достоверности гипотезу проверяют другими методами или повторяют эксперимент, увеличив объём выборки. Отвергают гипотезу более категорично, чем принимают. Действительно, если удаётся привести пример, противоречащий некоторому общему утверждению, то само утверждение признаётся ложным.
Нахождение левосторонней и двусторонней критических областей тоже сводится к определению критических точек. Критическая точка kкр для левосторонней критической об-
ласти определяется из условия
P{K < kкр} =α .
Для определения двусторонней критической области следует найти две критические точки k1 и k2 , причём k2 > k1 . Эти точки должны удовлетворять условию
P{K < k1} + P{K > k2 } =α .
Ясно, что критические точки k1 и k2 могут быть выбраны бесчисленным числом способов. Если же имеются основания выбрать симметричные относительно нуля критические точки −kкр и kкр ( kкр > 0 ), то будет иметь место равенство
P{K < −kкр} = P{K > kкр}.
Следовательно, мы можем записать соотношение
P{K > kкр} = α2 ,
которое и служит для нахождения критических точек двусторонней критической области. Мощностью критерия называют вероятность попадания критерия в критическую об-
ласть при условии, что справедлива конкурирующая гипотеза. Иными словами, мощность критерия – это вероятность того, что нулевая гипотеза будет отвергнута, если верна конкурирующая гипотеза. Пусть для проверки гипотезы принят определённый уровень значимости α и выборка имеет фиксированный объём n . Возможность варьировать остаётся лишь в выборе критической области. Покажем, что её целесообразно построить так, чтобы мощность критерия была максимальной. Если через β обозначить вероятность ошибки второго рода
(т.е. события «принята нулевая гипотеза при справедливости конкурирующей»), то мощность критерия будет равна 1− β . При возрастании мощности критерия 1− β уменьшается
вероятность β совершить ошибку второго рода. Следовательно, если уровень значимости α уже выбран, то критическую область нужно строить так, чтобы мощность критерия 1− β
была максимальной. Выполнение этого требования будет обеспечивать минимальную ошибку второго рода.
ЗамечаниеU 3.U Понятно, что чем меньше вероятности ошибок первого и второго рода, тем лучше для исследователя. Однако при заданном объёме выборки невозможно одновременно уменьшить α и β , т.к. при снижении α вероятность β будет возрастать. Например,

67
если положить α = 0 , то будут приниматься все гипотезы (как правильные, так и неправильные), что, естественно, приведёт к росту вероятности ошибки второго рода β . Как же наи-
более целесообразно выбирать α ? Исследователю нужно учитывать «тяжесть последствий» своего решения для каждого конкретного случая.
В дальнейшем будет рассмотрена лемма Неймана-Пирсона. Согласно ей при фиксированном уровне значимости α можно построить критическую область, для которой мощность критерия 1− β будет максимальной.
ЗамечаниеU 4.U Единственный способ одновременного уменьшения вероятностей ошибок первого и второго рода состоит в увеличении объёма выборок.

68
Лекция 6. ПРОВЕРКАU СТАТИСТИЧЕСКИХ ГИПОТЕЗ О РАВЕНСТВЕ ДИСПЕРСИЙ И СРЕДНИХ U
План
1.Сравнение двух дисперсий нормальных генеральных совокупностей.
2.Сравнение исправленной выборочной дисперсии с гипотетической генеральной
дисперсией нормальной совокупности.
3.Сравнение двух средних нормальных генеральных совокупностей, дисперсии ко-
торых известны.
4.Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых неизвестны и одинаковы. Случай малых независимых выборок.
1.Часто на практике возникает задача сравнения дисперсий. Это связано с потребностью сопоставлять точность приборов, инструментов, самих методов измерений и т.д. Естественно, предпочтительнее тот инструмент, который обеспечивает наименьшее рассеяние результатов измерений, т.е. наименьшую дисперсию.
Пусть генеральные совокупности X и Y распределены нормально. Из совокупностей
извлечены выборки объема n1 и n2 , соответственно. По ним найдены исправленные выбо-
рочные дисперсии sX 2 и sY 2 . Требуется по исправленным дисперсиям при заданном уровне
значимости α проверить нулевую гипотезу. Она состоит в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой:
H0 : DX = DY .
В силу того, что исправленные дисперсии являются несмещенными оценками генеральных дисперсий, т.е.
Ms |
2 = DX , Ms 2 |
= DY , |
X |
Y |
|
нулевую гипотезу можно записать следующим образом:
H0 : MsX 2 = MsY 2 .
Т.о. требуется проверить, что математические ожидания исправленных выборочных дисперсий равны между собой. Обычно исправленные дисперсии оказываются различными. Значимо (существенно) или незначимо различаются исправленные дисперсии?
Если окажется, что нулевая гипотеза справедлива, т.е. генеральные дисперсии одинаковы, то различие исправленных дисперсий незначимо и объясняется случайными причинами, в частности случайным отбором объектов выборки. Например, если различие исправленных выборочных дисперсий результатов измерений, выполненных двумя приборами, оказалось незначимым, то приборы имеют одинаковую точность. Если же нулевая гипотеза отвергнута, т.е. генеральные дисперсии неодинаковы, то различие исправленных дисперсий значимо и не может быть объяснено случайными причинами.
В качестве критерия проверки нулевой гипотезы о равенстве генеральных дисперсий принимают отношение большей исправленной дисперсии к меньшей, т.е. случайную величину
F = |
s |
2 |
. |
б |
|||
|
|||
|
sм |
2 |
|
Величина F при условии справедливости нулевой гипотезы имеет распределение ФишераСнедекора со степенями свободы k1 = n1 −1 и k2 = n2 −1 , где n1 – объем выборки, по которой
вычислена большая исправленная дисперсия, n2 – объем выборки, по которой найдена
меньшая дисперсия. Распределение Фишера-Снедекора зависит только от чисел степеней свободы и не зависит от других параметров. Для него имеются специальные таблицы. Критическая область строится в зависимости от вида конкурирующей гипотезы.

69
В качестве первого случая рассмотрим нулевую гипотезу H0 : DX = DY и конкурирующую гипотезу H1 : DX > DY . Построим правостороннюю критическую область. Потре-
буем, чтобы вероятность попадания критерия F в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости:
P{F > Fкр (α; k1 , k2 )} =α .
Критическая точка Fкр (α; k1 , k2 ) находится по таблице критических точек распределения
Фишера-Снедекора. Обозначим отношение большей из наблюдаемых исправленных дисперсий к меньшей, как Fн . Сформулируем правило проверки нулевой гипотезы.
Для того чтобы при заданном уровне значимости проверить нулевую гипотезу H0 : DX = DY о равенстве генеральных дисперсий нормальных совокупностей при конкури-
рующей гипотезе H1 : DX > DY , надо вычислить отношение большей исправленной дисперсии к меньшей, т.е.
s 2
Fн = sб 2 .
м
По таблице критических точек распределения Фишера-Снедекора находят Fкр (α;k1 , k2 ) . Если Fн < Fкр , то нет оснований отвергать нулевую гипотезу. В противном же случае её отвер-
гают. Если использовать статистические функции из Microsoft Excel, то для нахождения Fкр (α;k1 , k2 ) надо вычислять FРАСПОБР(α; k1 ; k2 ). В Maple 6 для этих целей служит функ-
ция stats[statevalf,icdf,fratio[ k1, k2 ]](1-α ).
ПримерU 1.U По двум независимым выборкам с объёмами n1 =13 и n2 =18 , которые извлечены из нормальных генеральных совокупностей X и Y , найдены исправленные выборочные дисперсии sX 2 =12 и sY 2 = 6 . При уровне значимости α = 0,05 проверить нулевую гипотезу H0 : DX = DY о равенстве генеральных дисперсий при конкурирующей гипотезе
H1 : DX > DY .
Решение. Найдем отношение большей исправленной дисперсии к меньшей:
F = |
12 |
= 2 . |
|
|
|
|
|
|
|
||
н |
6 |
|
|
|
|
|
|
|
|
|
|
Далее используем таблицу критических точек распределения F Фишера-Снедекора. По за- |
|||||
данному уровню значимости α = 0,05 и числам степеней |
свободы |
k1 =13 −1 =12 |
и |
||
k2 =18 −1 =17 находим критическую точку Fкр (0,05;12,17) = 2,38 . |
Т.к. |
Fн < Fкр , то |
нет |
||
оснований отвергать нулевую гипотезу о равенстве генеральных дисперсий. Использование Microsoft Excel и Maple 6 приводит к аналогичным результатам:
Fкр (0,05;12,17) =FРАСПОБР( 0,05;12;17 )=2,38065;
Fкр (0,05;12,17) =stats[statevalf,icdf,fratio[12,17]](1-0.05)=2.38065.
В качестве второго случая рассмотрим нулевую гипотезу H0 : DX = DY и конкурирующую гипотезу H1 : DX ≠ DY . В этом случае надо строить двустороннюю критическую
область. Можно доказать, что наибольшая мощность (вероятность попадания критерия в критическую область при справедливости конкурирующей гипотезы) достигается тогда, когда вероятность попадания критерия в каждый из двух интервалов критической области равна α / 2 . Обозначим через F1 левую границу критической области и через F2 – правую. То-
гда должны выполняться соотношения |
|
|
|
|
P{F < F } = α |
, |
P{F > F } = α . |
||
1 |
2 |
|
2 |
2 |
|
|
|
||

70
Правую критическую точку F2 = Fкр (α / 2;k1 , k2 ) находят по таблице критических точек рас-
пределения Фишера-Снедекора.
Оказывается, что левую критическую точку можно и не отыскивать. Достаточно найти правую критическую точку F2 при уровне значимости, вдвое меньшем заданного. Тогда не только вероятность попадания критерия в «правую часть» критической области (т.е. правее F2 ) равна α / 2 , но и вероятность попадания этого критерия в «левую часть» критической области (т.е. левее F1 ) также равна α / 2 . Т.к. эти события несовместны, то вероятность по-
падания рассматриваемого критерия во всю двустороннюю критическую область будет равна
α / 2 +α / 2 =α .
Сформулируем правило проверки нулевой гипотезы о равенстве генеральных дисперсий нормально распределенных совокупностей при конкурирующей гипотезе H1 : DX ≠ DY . Для этого нужно вычислить отношение большей исправленной дисперсии к меньшей, т.е.
Fн = sб2 . По таблице критических точек распределения Фишера-Снедекора по уровню зна- sм2
чимости α / 2 (вдвое меньшем заданного) и числам степеней свободы k1 и k2 ( k1 – число степеней свободы большей дисперсии) найти критическую точку Fкр (α / 2;k1 , k2 ) . Если Fн < Fкр , то нет оснований отвергать нулевую гипотезу. В противном же случае её отверга-
ют.
ПримерU 2.U По двум независимым выборкам с объёмами n1 =13 и n2 = 9 , которые извлечены из нормальных генеральных совокупностей X и Y , найдены исправленные выборочные дисперсии sX 2 =1,2 и sY 2 = 0,3 . Требуется при уровне значимости α = 0,1 проверить нулевую гипотезу H0 : DX = DY о равенстве генеральных дисперсий при конкурирующей гипотезе H1 : DX ≠ DY .
Решение. Найдем отношение большей исправленной дисперсии к меньшей:
Fн = 10,,23 = 4 .
Теперь используем таблицу критических точек распределения F Фишера-Снедекора. По заданному уровню значимости α / 2 = 0,1/ 2 = 0,05 и числам степеней свободы k1 =13 −1 =12 и
k2 = 9 −1 = 8 находим критическую точку Fкр (0,05;12,8) = 3,28 . Использование Microsoft Excel
и Maple 6 приводит к аналогичным результатам:
Fкр (0,05;12,8) = FРАСПОБР( 0,05;12;8 )=3,28394;
Fкр (0,05;12,8) = stats[statevalf,icdf,fratio[12,8]](1-0.05)=3.28394.
Т.к. Fн > Fкр , то нулевую гипотезу о равенстве генеральных дисперсий отвергаем. Другими
словами, выборочные исправленные дисперсии различаются значимо. Например, если бы рассматриваемые дисперсии характеризовали точность двух методов измерений, то следует предпочесть тот метод, который имеет меньшую дисперсию (судя по нашему примеру 0,3).
2. Рассмотрим теперь задачу сравнения исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности.
Пусть генеральная совокупность распределена нормально, причем генеральная дисперсия хотя и неизвестна, но имеются основания предполагать, что она равна гипотетиче-
скому (предполагаемому) значению. На практике σ0 2 устанавливается на основании предшествующего опыта или теоретически. Пусть из генеральной совокупности извлечена вы-
борка объема n и по ней найдена исправленная выборочная дисперсия s 2 с k = n −1 степенями свободы. Требуется по исправленной дисперсии при заданном уровне значимости про-

71
верить нулевую гипотезу, состоящую в том, что генеральная дисперсия рассматриваемой совокупности равна гипотетическому значению σ0 2 . Т.к. s 2 является несмещенной оценкой генеральной дисперсии, имеем нулевую гипотезу
H0 : Ms 2 =σ0 2 .
Итак, требуется проверить, что математическое ожидание исправленной дисперсии равно гипотетическому значению генеральной дисперсии. Другими словами, надо установить, значимо или незначимо различаются исправленная выборочная и гипотетическая генеральная дисперсии.
На практике рассматриваемая гипотеза проверяется, если нужно проверить точность приборов, инструментов, станков, методов исследования и устойчивость технологических процессов. Например, известна допустимая характеристика рассеяния контролируемого раз-
мера деталей, изготавливаемых станком-автоматом, равная σ0 2 . Если найденная по выборке характеристика окажется значимо больше σ0 2 , то станок нуждается в наладке.
Критерием проверки нулевой гипотезы является случайная величина
χ2 = s 2 (n −1) .
σ0 2
Критическая область строится в зависимости от вида конкурирующей гипотезы. Рассмотрим первый случай. Пусть нулевая гипотеза H0 :σ 2 =σ0 2 . Конкурирующая
гипотеза H1 :σ 2 >σ0 2 . В этом случае строят правостороннюю критическую область и тре-
буют, чтобы выполнялось соотношение
P{χ2 > χкр2 (α; k)} =α .
Сформулируем правило проверки нулевой гипотезы. Надо вычислить наблюдаемое
2 |
|
s 2 |
(n −1) |
|
2 |
|
|
значение критерия χн |
= |
|
|
|
. Затем по таблице критических точек распределения χ |
|
, по |
|
σ |
2 |
|
||||
|
|
|
|
0 |
|
|
|
заданному уровню значимости α и числу степеней свободы k = n −1 найти критическую
точку χкр2 (α; k) . В Microsoft Excel |
критическая |
точка находится следующим |
образом |
|||||||||||
χкр2 (α;k) =ХИ2ОБР( k ;α ). В Maple 6 она определяется как |
|
|
|
|||||||||||
|
|
|
χкр2 (α; k) = stats[statevalf, icdf, chisquare[ k ]](1−α ). |
|
||||||||||
Если χн2 < χкр2 , |
то нет оснований отвергать нулевую гипотезу. В противном случае нулевую |
|||||||||||||
гипотезу отвергают. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
ПримерU |
3.U Из нормальной генеральной совокупности |
извлечена выборка |
объема |
||||||||||
|
|
|
|
|||||||||||
n =15 и по ней найдена исправленная выборочная дисперсия s 2 |
=14,9 . Требуется при уров- |
|||||||||||||
не значимости α = 0,01 проверить нулевую гипотезу H0 :σ 2 =σ0 |
2 =14,1, приняв в качестве |
|||||||||||||
конкурирующей гипотезы H1 :σ 2 |
>14,1 . |
|
|
|
|
|
|
|
||||||
|
Решение. Найдем наблюдавшееся значение критерия: |
|
|
|
||||||||||
|
|
2 |
= |
s 2 |
(n −1) |
= |
14,9 14 |
≈14,79 . |
|
|
|
|||
|
|
|
χн |
|
|
|
|
|
|
|
|
|||
|
|
|
|
σ |
2 |
14,1 |
|
|
|
|
||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
Согласно конкурирующей гипотезе, критическая область является правосторонней. Из таблиц по уровню значимости α = 0,01 и числу степеней свободы k = n −1 =15 −1 =14 находим
критическую |
точку |
χкр2 (0,01;14) = 29,1. |
В |
Microsoft |
Excel |
получаем |
χкр2 (0,01;14) =ХИ2ОБР(14;0,01)=29,141. В Maple |
6 имеем |
χкр2 (0,01;14) =stats[statevalf, icdf, |
||||
chisquare[14]](1-0.01)=29.141. Т.к. χн2 < χкр2 , то нет оснований отвергать нулевую гипотезу.

72
Другими словами, различие между исправленной дисперсией 14,9 и гипотетической генеральной дисперсией 14,1 – незначимое.
Рассмотрим теперь второй основной случай проверки гипотез. Нулевая гипотеза H0 :σ 2 =σ0 2 . Конкурирующая гипотеза H1 :σ 2 ≠σ0 2 . В этом случае строят двустороннюю
критическую область. При этом исходят из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости α . Критические точки – левую и правую границы критической области
– находят, требуя, чтобы вероятность попадания критерия в каждый из двух интервалов критической области была равна α / 2 :
P{χ2 < χлев2 |
.кр (α / 2;k)} =α / 2, P{χ2 > χправ2 |
.кр (α / 2;k)} =α / 2 . |
В таблице критических точек распределения указаны лишь «правые» критические точки, поэтому возникает кажущееся затруднение в отыскании «левой» критической точки. Это за-
труднение |
легко преодолеть, если принять во |
внимание, что события χ2 < χлев2 |
.кр и |
|||||
χ2 > χлев2 |
.кр |
противоположны и, следовательно, |
|
|
|
|
||
|
|
P{χ2 < χлев2 |
.кр} + P{χ2 |
> χлев2 |
.кр} =1 . |
|
||
Отсюда |
|
P{χ2 > χлев2 |
.кр} =1− P{χ2 < χлев2 |
|
|
|
||
|
|
.кр} =1−α / 2 . |
|
|||||
Т.е. левую критическую точку можно искать как правую (и значит, ее можно найти по таблице), исходя из требования, чтобы вероятность попадания критерия в интервал, расположенный правее этой точки, была равна 1−α / 2 .
Сформулируем правило проверки нулевой гипотезы. Для того чтобы при заданном уровне значимости α проверить нулевую гипотезу о равенстве неизвестной генеральной
дисперсии σ 2 нормальной совокупности гипотетическому значению σ0 2 при конкурирую-
щей гипотезе H1 :σ 2 ≠σ0 2 , надо вычислить наблюдаемое значение критерия χн2 = |
s 2 (n −1) |
|
||||||||
|
||||||||||
|
|
|
|
|
|
|
|
σ |
2 |
|
|
|
|
|
|
|
|
|
|
0 |
|
и по таблице найти левую критическую точку χлев2 |
.кр = χкр2 |
(1−α / 2; k) и правую критическую |
||||||||
точку χправ2 |
.кр = χкр2 (α / 2;k) . Если окажется, что χлев2 |
.кр < χн2 |
< χправ2 |
.кр , то нет оснований отверг- |
||||||
нуть нулевую гипотезу. Если же окажется, что χн2 < χлев2 |
.кр |
или χн2 > χправ2 |
.кр , то нулевую гипо- |
|||||||
тезу отвергают.
ПримерU 4.U Из нормальной генеральной совокупности извлечена выборка объема
n =16 и по ней найдена исправленная выборочная дисперсия s 2 =10,9 . Требуется при уровне значимости α = 0,02 проверить нулевую гипотезу H0 :σ 2 =σ0 2 =14 , приняв в качестве
конкурирующей H1 :σ 2 ≠14 .
Решение. Найдем наблюдавшееся значение критерия:
2 |
= |
s 2 |
(n −1) |
= |
10,9 15 |
≈11,68 . |
|
χн |
|
|
|
|
|||
|
σ |
2 |
14 |
||||
|
|
|
|
0 |
|
|
|
Судя по конкурирующей гипотезе, критическая область будет двусторонней. По таблицам находим критические точки:
χлев2 |
.кр = χкр2 (1−0,02 / 2;15) = χкр2 (0,99;15) = 5,23 |
|
и |
|
|
χправ2 |
.кр = χкр2 (0,02 / 2;15) = χкр2 (0,01;15) = 30,6 . |
|
Т.к. наблюдавшееся значение критерия принадлежит области принятия гипотезы: 5,23<11,68<30,6, то нет оснований её отвергать. Другими словами, исправленная выборочная
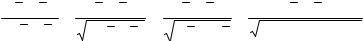
73
дисперсия s 2 =10,9 незначимо отличается от гипотетической генеральной дисперсии
σ0 2 =14 .
Втретьем случае конкурирующая гипотеза имеет вид H1 :σ 2 <σ0 2 . При такой кон-
курирующей гипотезе находят критическую точку χкр2 (1−α;k) . Если окажется, что χн2 > χкр2 (1−α;k) , то нет оснований отвергать нулевую гипотезу. В противном случае её отвергают.
3. На практике часто возникает необходимость сравнить средние статистических со-
вокупностей. Рассмотрим вопрос сравнения средних двух нормальных генеральных совокуп-
ностей, дисперсии которых известны. Нами будет рассмотрен случай независимых выборок. Итак, пусть генеральные совокупности X и Y распределены нормально и их дисперсии известны (например, из предшествующего опыта или найдены теоретически). По незави-
симым выборкам объема n и m , соответственно, извлеченным из этих совокупностей, рассчитаны выборочные средние x и y . Необходимо по выборочным средним при заданном
уровне значимости α проверить нулевую гипотезу, состоящую в том, что генеральные средние (математические ожидания) рассматриваемых совокупностей равны между собой, т.е.
H0 : MX = MY .
Т.к. выборочные средние являются несмещенными оценками генеральных средних (т.е. Mx = MX , My = MY ), то нулевую гипотезу можно записать так:
H0 : Mx = My .
Т.о. требуется проверить, что математические ожидания выборочных средних равны между собой. Такая задача ставится потому, что, как правило, выборочные средние оказываются различными. Возникает вопрос: значимо или незначимо различаются они?
Если окажется, что нулевая гипотеза справедлива, т.е. генеральные средние одинаковы, то различие выборочных средних незначимо и объясняется случайными причинами (случайным отбором элементов выборки и т.д.). Например, если физические величины имеют одинаковые истинные размеры, а средние арифметические результатов измерений этих величин различны, то это различие незначимое. Если же нулевая гипотеза отвергнута, т.е. генеральные средние неодинаковы, то различие выборочных средних значимо и не может быть объяснено случайными причинами, а объясняется тем, что сами генеральные средние (математические ожидания) различны. Например, если среднее арифметическое x результатов измерений первой физической величины значимо отличается от среднего арифметического y результатов измерений второй физической величины, то это означает, что истинные раз-
меры (математические ожидания) этих величин различны.
В качестве критерия проверки нулевой гипотезы примем случайную величину
Z = |
x − y |
= |
x − y |
= |
x − y |
= |
x − y |
. |
|
σ(x − y) |
|
D(x − y) |
|
Dx + Dy |
|
DX / n + DY / m |
|
Критерий Z – нормированная нормальная случайная величина. Действительно, величина распределена нормально, так как является линейной комбинацией нормально распределенных величин x и y . Сами эти величины распределены нормально как выборочные средние,
найденные по выборкам, извлеченным из нормальных генеральных совокупностей. Z – нормированная величина, т.к. при справедливости нулевой гипотезы MZ = 0 и, поскольку выборки независимы, σ(Z ) =1 .
Как и ранее критическая область строится в зависимости от вида конкурирующей гипотезы.
Случай первый: нулевая гипотеза H0 : MX = MY , конкурирующая гипотеза H1 : MX ≠ MY . В этом случае строят двустороннюю критическую область. При этом требу-
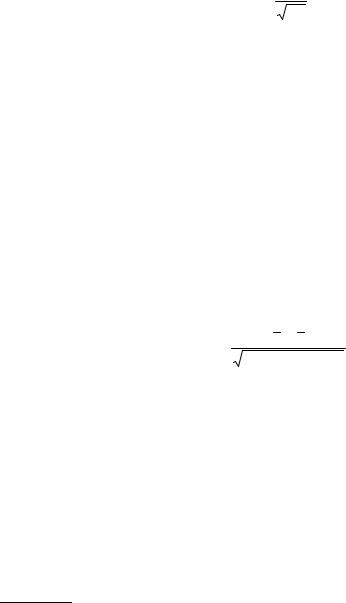
74
ют, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна заданному уровню значимости α .
Наибольшая мощность критерия достигается тогда, когда левая и правая критические точки выбраны так, что вероятность попадания критерия в каждый из двух интервалов критической области равна α / 2 :
P{Z < zлев.кр} =α / 2, P{Z > zправ.кр} =α / 2 .
Т.к. Z – нормированная нормальная величина, а распределение такой величины симметрично относительно нуля, то критические точки также симметричны относительно нуля. Обозначим правую границу двусторонней критической области через zкр , тогда левая граница
равна (−zкр ) . Поэтому достаточно найти правую границу, чтобы найти саму двустороннюю критическую область Z < −zкр , Z > zкр и область принятия нулевой гипотезы (−zкр; zкр ) .
Интегральная функция Лапласа Φ(z) = |
1 |
∫z |
e−t 2 / 2 dt определяет вероятность попада- |
|
2π |
0 |
|
ния нормированной нормальной случайной величины Z в интервал (0; z) : |
|||
P{0 < Z < z} = Φ(z) .
В силу симметрии этого распределения относительно нуля, имеем
P{0 < Z < zкр} + P{Z > zкр} =1/ 2 .
Т.е.
Φ(zкр ) +α / 2 =1/ 2 ,
откуда получаем
Φ(zкр ) = (1−α) / 2 .
Теперь, обозначив через Zн наблюдаемое значение критерия (т.е. вычисленное по
данным выборки), сформулируем правило проверки нулевой гипотезы.
Для того, чтобы при заданном уровне значимости α проверить нулевую гипотезу H0 : MX = MY о равенстве математических ожиданий двух нормальных генеральных сово-
купностей с известными дисперсиями при конкурирующей гипотезе H1 : MX ≠ MY , надо
вычислить наблюдаемое значение критерия |
|
||||||
|
|
|
|
|
Zн = |
x − y |
. |
|
|
|
|
|
DX / n + DY / m |
||
|
|
|
|
|
|
|
|
и по таблице интегральной функции Лапласа найти критическую точку zкр из условия |
|||||||
|
|
|
|
|
Φ(zкр ) = (1−α) / 2 . |
|
|
Если окажется, |
что |
|
Zн |
|
< zкр , то нет оснований отвергать нулевую гипотезу. В противном же |
||
|
|
||||||
случае её нужно отвергнуть. |
|
|
|||||
Если использовать статистические функции из Microsoft Excel, то для нахождения zкр |
|||||||
надо вычислять |
|
|
|
|
zкр =НОРМСТОБР( (1−α) / 2 +0,5 ). |
||
|
|
|
|
|
|||
В Maple 6 для нахождения zкр вычисляют |
|
|
|||||
|
|
|
zкр =stats[statevalf, icdf, normald[0,1]]( (1−α) / 2 +0.5 ). |
||||
ПримерU |
1.U По двум независимым выборкам, объемы которых соответственно равны |
||||||
n = 50 и m = 40 , извлеченным из нормальных генеральных совокупностей, найдены выборочные средние x =105 и y =110 . Генеральные дисперсии известны: DX =10 и DY = 8,25 .
Требуется при уровне значимости α = 0,01 проверить нулевую гипотезу H0 : MX = MY , при конкурирующей гипотезе H1 : MX ≠ MY .
Решение. Найдём наблюдаемое значение критерия

|
|
|
|
|
|
75 |
Zн = |
105 −110 |
= |
−5 |
= |
−5 |
= −7,8444 . |
|
10 / 50 +8,25 / 40 |
|
0,2 +0,20625 |
0,6374 |
|
|
По условию, конкурирующая гипотеза имеет вид |
H1 : MX ≠ MY , поэтому критическая об- |
|||||
ласть – двусторонняя. Найдем правую критическую точку из условия
Φ(zкр ) = (1−0,01) / 2 = 0,495 .
По таблице интегральной функции Лапласа zкр = 2,58 . Если использовать Microsoft Excel, то zкр =НОРМСТОБР( (1−0,01) / 2 +0,5 )=2,5758.
При использовании Maple 6, имеем
zкр =stats[statevalf, icdf, normald[0,1]]( (1−0.01) / 2 +0.5 )=2.5758.
Т. к. Zн > zкр , то нулевая гипотеза отвергается. Иными словами, выборочные средние разли-
чаются значимо.
В качестве второго случая рассмотрим нулевую гипотезу H0 : MX = MY и конкурирующую гипотезу H1 : MX > MY . На практике такой случай имеет место, если профессио-
нальные соображения позволяют предположить, что генеральная средняя одной совокупности больше генеральной средней другой. Например, пусть генеральная средняя характеризует объём выпуска продукции. Если технологический процесс был усовершенствован, то естественно допустить, что это приведет к увеличению объёма выпуска продукции.
В этом случае строят правостороннюю критическую область. Причём, исходят из требования, чтобы вероятность попадания критерия в эту область (в предположении справедливости нулевой гипотезы) была равна заданному уровню значимости:
P{Z > zкр} =α .
Критическая точка находится следующим образом. Воспользовавшись симметрией функции распределения стандартной нормальной случайной величины относительно нуля, получаем
P{0 < Z < zкр} + P{Z > zкр} =1/ 2 .
Т.о.
Φ(zкр ) +α =1/ 2 ,
откуда имеем
Φ(zкр ) = (1−2α) / 2 .
Из последнего соотношения по таблицам интегральной функции Лапласа или программными средствами находят точку zкр .
Определим правило проверки нулевой гипотезы. Для того чтобы при заданном уровне значимости α проверить нулевую гипотезу H0 : MX = MY о равенстве математических ожи-
даний двух нормальных генеральных совокупностей с известными дисперсиями при конкурирующей гипотезе H1 : MX > MY , надо вычислить наблюдавшееся значение критерия
Zн = |
x − y |
|
DX / n + DY / m |
||
|
и по таблице интегральной функции Лапласа найти критическую точку zкр из условия
Φ(zкр ) = (1−2α) / 2 .
Если окажется, что Zн < zкр , то нет оснований отвергать нулевую гипотезу. В противном же
случае её нужно отвергнуть.
ПримерU 2.U По двум независимым выборкам, объемы которых соответственно равны n =12 и m =12 , извлеченным из нормальных генеральных совокупностей, найдены выборочные средние x =15 и y =12,9 . Генеральные дисперсии известны: DX = 20 и DY =17 .
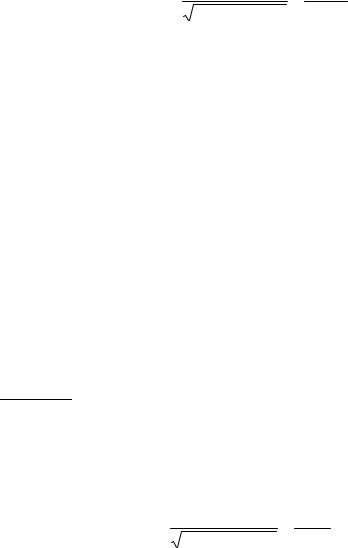
76
При уровне значимости α = 0,05 проверить нулевую гипотезу H0 : MX = MY при конкурирующей гипотезе H1 : MX > MY .
Решение. Найдем наблюдаемое значение критерия:
Zн |
= |
15 −12,9 |
/12 |
≈ |
2,1 |
≈1,196 . |
Найдем критическую точку zкр |
|
20 /12 +17 |
|
1,7559 |
|
|
из условия |
|
|
|
|
||
|
|
Φ(zкр ) = (1−0,1) / 2 = 0,45 . |
||||
По таблице интегральной функции Лапласа zкр =1,64 . Т.к. Zн < zкр , то нет оснований от-
вергнуть нулевую гипотезу. Другими словами, выборочные средние различаются незначимо. Третий случай: нулевая гипотеза H0 : MX = MY , конкурирующая гипотеза
H1 : MX < MY . Этот случай подразумевает построение левосторонней критической области.
При этом нужно исходить из требования, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости:
P{Z < z′кр} =α .
Т.к. критерий Z распределен симметрично относительно нуля, то z′кр = −zкр .
Правило проверки нулевой гипотезы будет следующим. При конкурирующей гипотезе H1 : MX < MY надо вычислить Zн . Из таблицы интегральной функции Лапласа найти
«вспомогательную точку» zкр по равенству Φ(zкр ) = (1−2α) / 2 и положить z′кр = −zкр . Если окажется, что Zн > −zкр , то нет оснований отвергать нулевую гипотезу. В противном же слу-
чае её нужно отвергнуть.
ПримерU 3.U По двум независимым выборкам, объемы которых соответственно равны n = 55 и m = 55 , извлеченным из нормальных генеральных совокупностей, найдены выборочные средние x =139 и y =151 . Генеральные дисперсии известны: DX = 30 и DY = 21.
При уровне значимости α = 0,01 проверить нулевую гипотезу H0 : MX = MY , при конкурирующей гипотезе H1 : MX < MY .
Решение. Найдем наблюдаемое значение критерия:
Zн = |
139 −151 |
≈ −12 ≈ −12,4611. |
|
|
|
30 / 55 + 21/ 55 |
0,963 |
|
|
Определим «вспомогательную точку» zкр из условия |
|
|
||
|
Φ(zкр ) = (1−0,02) / 2 = 0,49 . |
|
|
|
По таблице интегральной функции Лапласа zкр = 2,33 . Т.о., |
′ |
. В силу того, |
||
zкр = −zкр = −2,33 |
||||
что Zн < −zкр , то нулевую гипотезу следует отвергнуть. Другими словами, выборочная средняя x значимо меньше выборочной средней y .
Мы закончили рассмотрение случая, в котором предполагалось, что генеральные совокупности X и Y распределены нормально и их дисперсии известны. При этих предположениях, в случае справедливости нулевой гипотезы о равенстве средних и независимых выборках, критерий Z распределён нормально с параметрами 0 и 1. Если же хотя бы одно из перечисленных требований не выполняется, то описанный метод сравнения средних неприменим.
В то же время, если независимые выборки имеют большой объем (не менее 30 каждая), то выборочные средние x и y распределены приближенно нормально. Выборочные
дисперсии sX 2 и sY 2 являются достаточно хорошими оценками генеральных дисперсий DX
и DY , соответственно. В этом смысле их можно считать известными приближенно. Тогда критерий

77
Z ′ = |
|
x − y |
|
|
|
2 / n + s |
2 |
|
|
s |
X |
/ m |
||
|
|
Y |
|
распределен приближенно нормально с параметрами MZ ′ = 0 (при условии справедливости нулевой гипотезы) и σ(Z ′) =1 (если выборки независимы). В итоге мы можем сделать сле-
дующие выводы: 1) если генеральные совокупности распределены нормально, а дисперсии их неизвестны; 2) если генеральные совокупности не распределены нормально и дисперсии их неизвестны, причем выборки имеют большой объем и независимы, тогда можно сравнивать средние так, как описано ранее, заменив при этом точный критерий приближенным критерием. Т.е. наблюдаемое значение приближенного критерия будет равно
|
|
|
|
|
|
|
Zн′ |
= |
x − y |
. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
sX 2 / n + sY 2 / m |
|
|
|
ЗамечаниеU |
1.U Поскольку рассматриваемый критерий – приближённый, к его выводам |
|||||||
следует |
относиться |
осторожно. |
|
|
|
|||||
|
|
ПримерU |
4.U По двум независимым выборкам, объемы которых соответственно равны |
|||||||
n =110 |
|
|
x = 30 , y = 29 и выборочные дисперсии |
|||||||
и m =140 , найдены выборочные средние |
||||||||||
sX |
2 =16 , sY |
2 = 27 . Необходимо при уровне значимости α = 0,05 проверить нулевую гипоте- |
||||||||
зу H0 : MX = MY , при конкурирующей гипотезе H1 : MX > MY . |
||||||||||
|
|
Решение. Найдем наблюдаемое значение критерия: |
||||||||
|
|
|
|
|
|
|
Zн′ = |
|
30 −29 |
≈1,7193 . |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
16 /110 + 27 /140 |
||||
По условию конкурирующая гипотеза имеет вид H1 : MX > MY . Следовательно, критическая область – правосторонняя. Найдем критическую точку zкр из условия
Φ(zкр ) = (1−2α) / 2 = (1−0,1) / 2 = 0,45 .
По таблице интегральной функции Лапласа zкр =1,64 . Т.к. Zн′ > zкр , то нулевая гипотеза отвергается. Другими словами, выборочные средние различаются значимо.
4. Пусть генеральные совокупности X и Y распределены нормально, причем их дисперсии неизвестны. Например, по выборкам малого объема нельзя получить хорошие оценки генеральных дисперсий. По этой причине метод сравнения средних, изложенный ранее, неприменим. Однако если дополнительно предположить, что неизвестные генеральные дисперсии равны между собой, то можно построить критерий (Стьюдента) сравнения средних. Например, если сравниваются средние размеры двух партий деталей, изготовленных на одном и том же станке, то естественно допустить, что дисперсии контролируемых размеров одинаковы. Возможен и случай, когда нет оснований считать дисперсии одинаковыми. Тогда перед тем как сравнивать средние, нужно, пользуясь критерием Фишера-Снедекора, проверить гипотезу о равенстве генеральных дисперсий.
Основная задача выглядет следующим образом. В предположении, что генеральные дисперсии одинаковы, требуется проверить нулевую гипотезу H0 : MX = MY . Т.е. требуется
выяснить, значимо или незначимо различаются выборочные средние x и y , найденные по
независимым малым выборкам объёмов n и m ( n < 30 , m < 30 ).
В качестве критерия проверки нулевой гипотезы рассмотрим случайную величину
T = |
x − y |
nm(n + m −2) . |
|
(n −1)sX 2 +(m −1)sY 2 |
n + m |
Величина T при справедливости нулевой гипотезы имеет t -распределение Стьюдента с k = n + m − 2 степенями свободы.
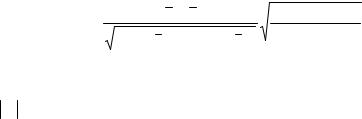
78
Как и ранее, в зависимости от вида конкурирующей гипотезы будем строить критическую область.
В первом из рассматриваемых случаев при нулевой гипотезе H0 : MX = MY конкурирующей будет гипотеза H1 : MX ≠ MY .
В этом случае строят двусторонюю критическую область. При этом, исходят из требования, чтобы вероятность попадания критерия T в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости α . Наибольшая мощность критерия достигается тогда, когда «левая» и «правую» критические точки выбраны так, что
P{T < tлев.кр} =α / 2, P{T > tправ.кр} =α / 2 .
Поскольку случайная величина T имеет распределение Стьюдента (симметричное относительно нуля), то и критические точки симметричны относительно нуля. Т.о., если обозначить правую границу двусторонней критической области через tдвуст.кр (α;k) , то левая гра-
ница равна (−tдвуст.кр (α;k)) . Следовательно, достаточно найти правую границу двусторонней
критической области, чтобы найти саму двустороннюю критическую область: T < −tдвуст.кр (α;k), T > tдвуст.кр (α;k) . При этом область принятия нулевой гипотезы определяется симметричным относительно нуля отрезком [−tдвуст.кр (α;k),tдвуст.кр (α;k)] .
Сформулируем правило проверки нулевой гипотезы.
Для того чтобы при заданном уровне значимости проверить нулевую гипотезу H0 : MX = MY о равенстве математических ожиданий двух нормальных генеральных сово-
купностей с неизвестными, но одинаковыми дисперсиями (случай независимых малых выбо-
рок) при конкурирующей гипотезе |
H1 : MX ≠ MY , |
надо вычислить наблюдаемое значение |
|
критерия Стьюдента: |
|
|
|
T = |
|
x − y |
nm(n + m −2) . |
н |
(n −1)sX 2 +(m −1)sY 2 |
n + m |
|
|
|||
Затем по таблице критических точек распределения Стьюдента при заданном уровне значимости α и числу степеней свободы k = n + m −2 найти критическую точку t (α;k) . Если
окажется, что Tн < tдвуст.кр (α; k) , то отвергать нулевую гипотезу нет оснований. В противном
случае её отвергают. |
|
|
|
|||
|
ПримерU |
5.U По двум независимым малым выборкам с объёмами n =13 , m =18 , кото- |
||||
рые |
|
|
Y , найдены выборочные |
|||
извлечены из нормальных генеральных совокупностей X , |
||||||
средние x = 4 , |
y = 3 и исправленные выборочные дисперсии sX |
2 |
=12 , sY |
2 = 6 . При уровне |
||
значимости α = 0,05 проверить нулевую гипотезу H0 : MX = MY о равенстве генеральных дисперсий при конкурирующей гипотезе H1 : MX ≠ MY .
Решение. Т.к. выборочные дисперсии различны, проверим предварительно нулевую гипотезу H0 : DX = DY о равенстве генеральных дисперсий, пользуясь критерием F Фише-
ра-Снедекора.
Найдем отношение большей исправленной дисперсии к меньшей:
Fн = 126 = 2 .
Дисперсия sX 2 значительно больше дисперсии sY 2 , поэтому в качестве конкурирующей примем гипотезу H1 : DX > DY . В этом случае критическая область – правосторонняя. По таблице критических точек распределения F Фишера-Снедекора при заданном уровне значимости α = 0,05 и числам степеней свободы k1 =13 −1 =12 и k2 =18 −1 =17 находим кри-
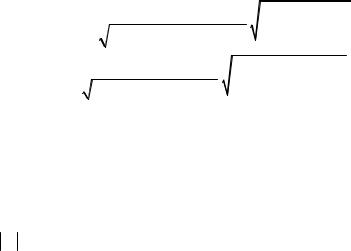
79
тическую точку Fкр (0,05;12,17) = 2,38 . Т.к. Fн < Fкр , то нет оснований отвергать нулевую
гипотезу о равенстве генеральных дисперсий.
Поскольку предположение о равенстве генеральных дисперсий выполняестя, сравним средние. Для этого вычислим наблюдаемое значение критерия Стьюдента:
T |
= |
|
x − y |
|
|
nm(n + m −2) = |
|
|
|
|
|
||||
н |
|
(n −1)sX 2 +(m −1)sY 2 |
n + m |
|
|||
|
|
|
|||||
= |
|
|
4 −3 |
13 18(13 +18 −2) |
≈ 0,9433. |
||
(13 |
−1)12 +(18 −1)6 |
|
|
13 +18 |
|||
|
|
|
|
||||
По условию, конкурирующая гипотеза имеет вид H1 : MX ≠ MY , поэтому критическая область – двустороняя. По уровню значимости α = 0,05 (двусторонняя критическая об-
ласть) и числу степеней свободы
k = n + m −2 =13 +18 −2 = 29
находим из приложения 6 по таблице критических точек распределения Стьюдента tдвуст.кр (0,05;29) = 2,045231 .
Т.к. Tн < tдвуст.кр (α; k) , то отвергать нулевую гипотезу о равенстве генеральных средних нет оснований. Иными словами, выборочные средние различаются незначимо.
Вместо таблиц можно использовать и программные средства. Например, в Maple 6 для нахождения критической точки (при двухсторонней критической области) следует применять функцию
tдвуст.кр (α;k) = stats[statevalf,icdf,studentst[ k ]](1−α / 2 ).
Если же использовать Microsoft Excel, то
tдвуст.кр (α;k) = СТЬЮДРАСПОБР(α ; k ).
Пример выполнен.
Рассмотрим второй случай. Нулевая гипотеза H0 : MX = MY . Конкурирующая гипотеза H1 : MX > MY . В этом случае строят правосторонюю критическую область. При этом,
исходят из требования, чтобы вероятность попадания критерия T в эту область в предположении справедливости нулевой гипотезы, была равна принятому уровню значимости:
P{T > tправ.кр} =α .
Критическую точку tправ.кр (α;k) находят по таблице приложения 6, по уровню значимости α ,
помещенному в нижней строке таблицы, и по числу степеней свободы k = n + m −2 . Если окажется, что Tн < tправ.кр (α;k) , то отвергать нулевую гипотезу нет оснований. В противном случае её отвергают.
В Maple 6 для нахождения критической точки (при односторонней критической области) следует применять ту же функцию, но с другим аргументом:
tправ.кр (α;k) = stats[statevalf,icdf,studentst[ k ]](1−α ).
Если же использовать Microsoft Excel, то
|
tправ.кр (α;k) = СТЬЮДРАСПОБР( 2α ; k ). |
Третий |
случай. Нулевая гипотеза H0 : MX = MY . Конкурирующая гипотеза |
H1 : MX < MY . В этом случае строят левосторонюю критическую область, исходя из требо- |
|
вания, чтобы |
P{T < tлев.кр} =α . Т.к. распределение Стьюдента симметрично относительно |
нуля, то tлев.кр (α;k) = −tправ.кр (α;k) . Нахождение критической точки tправ.кр (α;k) описывалось во втором случае. Если окажется, что Tн > −tправ.кр (α;k) , то отвергать нулевую гипотезу нет оснований. В противном случае её отвергают.

80
Лекция 7. КРИТЕРИИU СОГЛАСИЯU
План
1.Понятие критерия согласия.
2.Критерий согласия Пирсона.
3.Проверка гипотезы о нормальном распределении генеральной совокупности по
критерию Пирсона.
1.Рассмотрим один из вопросов, связанных с проверкой правдоподобия гипотез, а именно – вопрос о согласованности теоретического и статистического распределения. Если закон распределения неизвестен, но есть основания предположить, что он имеет определен-
ный вид (например, F0 (x) ), то проверяют нулевую гипотезу: генеральная совокупность распределена по закону F0 (x) . Более того, пусть данное статистическое распределение выровнено с помощью некоторой теоретической кривой f0 (x) . Как бы хорошо ни была подобрана
теоретическая кривая, между нею и статистическим распределением неизбежны некоторые расхождения. Возникает вопрос: объясняются ли эти расхождения только случайными обстоятельствами, связанными с ограниченным числом наблюдений, или они являются существенными и связаны с тем, что подобранная нами кривая плохо выравнивает данное статистическое распределение. Для ответа на такой вопрос служат т.н. «критерии согласия».
Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределением. Идея применения критериев согласия заключается в следующем. На основании данного статистического материала нам предстоит проверить гипотезу H0 , состоящую в том, что случайная величина X подчиняется некоторому определенному
закону распределения. Этот закон может быть задан в той или иной форме: например, в виде функции распределения F(x) или в виде совокупностей вероятностей pi , где pi – вероят-
ность того, что величина X попадет в пределы i -го разряда (интервала). Функция распределения F (x) является наиболее общей формой закона распределения. Поэтому будем форму-
лировать гипотезу H0 , как состоящую в том, что случайная величина X имеет известную функцию распределения F0 (x) . Т.е. относительно теоретической функции распределения (функции распределения генеральной совокупности) F (x) выдвигаются две непараметрические (см. лекцию 14 МС) гипотезы: простая нулевая H0 : F(x) = F0 (x) и сложная конкурирующая H1 : F (x) ≠ F0 (x) .
На практике применяют критерии согласия χ2 («хи-квадрат») Пирсона, Колмогорова
(Андрей Николаевич Колмогоров (1903-1987) – советский математик), Смирнова (Николай Васильевич Смирнов (1900-1966) – советский математик), ω2 («омега-квадрат») и др.
2. Наиболее часто употребим критерий Пирсона. Опишем, как он применяется к проверке гипотезы о нормальном распределении генеральной совокупности. Заметим, что этот критерий аналогично применяется и для других распределений, и этот факт – несомненное преимущество.
Итак, пусть проведена серия опытов, в результате которых получена выборка объёма n . По выборке составлено статистическое распределение:
Варианты xi |
x1 |
x2 |
… |
xs |
Эмпирические частоты ni |
n1 |
n2 |
… |
ns |
s
Естественно, что ∑ni = n . Кроме того, в предположении нормального распределения, мы
i=1
вычислили (а, сказать точнее, оценили) частоты ni′ теоретического распределения. При

81
уровне значимости α требуется проверить нулевую гипотезу H0 : генеральная совокупность
распределена нормально.
Будет ли случайным расхождение частот? Может быть, что расхождение случайно (незначимо) и объясняется либо малым числом наблюдений, либо способом их группировки, либо иными причинами. Возможно, что расхождение частот неслучайно (значимо) и объясняется тем, что теоретические частоты вычислены исходя из неверной гипотезы о нормальном распределении генеральной совокупности. Критерий Пирсона отвечает на поставленный вопрос. Однако, как и любой критерий, он не доказывает справедливости гипотезы, а лишь устанавливает на допустимом уровне значимости α ее согласие или несогласие с данными наблюдений.
Как и ранее, для того чтобы принять или отвергнуть гипотезу H0 , нам следует ввести
некоторую случайную величину U , характеризующую степень расхождения теоретического и статистического распределений. Величина U может быть выбрана различными способами. Например, в качестве U можно взять сумму квадратов отклонений теоретических частот ni′
от соответствующих наблюдаемых частот ni . Или же сумму тех же квадратов отклонений с некоторыми коэффициентами («весами»). Или же максимальное отклонение статистической функции распределения Fn ( x) от теоретической F (x) и т. д.
При использовании критерия согласия Пирсона для проверки нулевой гипотезы рас-
s |
(ni −ni′) |
2 |
|
сматривают случайную величину: χ2 = ∑ |
|
. Эта величина, действительно, является |
|
ni′ |
|
||
i=1 |
|
|
случайной, т.к. в различных опытах она принимает различные, заранее неизвестные значения. Понятно, что чем меньше различаются эмпирические и теоретические частоты, тем
меньше величина критерия χ2 . Следовательно, он в определённом смысле характеризует
близость эмпирического и теоретического распределений.
Обсудим сам вид критерия. Итак, возведением в квадрат разностей частот устраняют возможность взаимного погашения положительных и отрицательных разностей. Делением на ni′ достигают уменьшения каждого из слагаемых. В противном случае сумма была бы велика
и это приводило бы к отклонению нулевой гипотезы даже и тогда, когда она справедлива. Доказано, что при n → ∞ закон распределения введенной случайной величины независимо от того, какому закону подчинена генеральная совокупность, стремится к закону распреде-
ления χ2 с k степенями свободы. Число степеней свободы равно: k = s −1− r , где s – число
групп (частичных интервалов) выборки, r – число параметров предполагаемого распределения. Параметры оцениваются по данным выборки. Например, если предполагаемое распределение – нормальное, то оценивают два параметра – математическое ожидание и среднеквадратическое отклонение. Следовательно, r = 2 , поэтому число степеней свободы
k= s −3.
Всилу того, что односторонний критерий более категорично отвергает нулевую гипотезу, чем двусторонний, построим правостороннюю критическую область. При этом будем требовать, чтобы вероятность попадания критерия в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости α :
P{χ2 > χкр2 (α;k)} =α .
Обозначим наблюдаемое значение критерия χн2 и сформулируем правило проверки нулевой гипотезы.
3. Рассмотрим задачу проверки гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона.

82
ПравилоU .U Для того чтобы при заданном уровне значимости α проверить нулевую гипотезу H0 : генеральная совокупность распределена нормально, надо сначала вычислить тео-
ретические частоты ni′, а затем наблюдаемое значение критерия
χ2 = ∑s (ni −ni′)2 .
нi=1 ni′
Затем по таблице критических точек распределения χ2 (приложение 5) при заданном уровне значимости α и числе степеней свободы k = s −3 находят критическую точку χкр2 (α;k) . Если окажется, что χн2 < χкр2 , то нет оснований отвергать нулевую гипотезу. В противном слу-
чае её отвергают.
ЗамечаниеU 1.U Объем выборки должен быть достаточно велик, во всяком случае, не менее 50. Каждая группа должна содержать не менее 5-8 вариант. Малочисленные группы следует объединять в одну, суммируя частоты.
ЗамечаниеU 2.U Поскольку возможны ошибки первого и второго рода, в особенности, если согласование теоретических и эмпирических частот «слишком хорошее», следует проявлять осторожность, Например, можно повторить опыт, увеличить число наблюдений, воспользоваться другими критериями, построить график распределения, вычислить асимметрию и эксцесс.
ЗамечаниеU 3.U Для контроля вычислений формулу, по которой вычисляют наблюдаемое значение критерия, преобразуют к виду
|
|
|
s |
n |
2 |
|
|
|
|
χн2 = ∑ |
i |
|
−n , |
|
|
|
n′ |
|||
|
|
|
= |
|
||
|
|
|
i 1 |
|
i |
|
|
|
s |
s |
|
|
|
учитывая, что ∑ni = n и ∑ni′ = n . |
|
|
|
|||
|
|
i=1 |
i=1 |
|
|
|
|
ПримерU |
1.U При уровне значимости α = 0,05 проверить гипотезу о нормальном рас- |
||||
|
|
|
|
|
|
|
пределении генеральной совокупности, если известны эмпирические ni и теоретические ni′ частоты:
|
|
|
ni |
|
5 |
|
13 |
36 |
|
83 |
101 |
80 |
35 |
|
15 |
|
|
|
|||
|
|
|
ni′ |
|
4 |
|
15 |
40 |
|
79 |
97 |
75 |
33 |
25 |
|
|
|
||||
Решение. Вычисления необходимые для определения наблюдаемого значения крите- |
|||||||||||||||||||||
рия приведём в табл. 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Табл. 1. |
Расчёт наблюдаемого значения критерия Пирсона |
|||||||||||||
|
i |
|
ni |
|
ni′ |
|
|
ni −ni′ |
(ni −ni′)2 |
|
|
|
(ni −ni′)2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ni′ |
|
|
|
|
1 |
|
5 |
|
|
4 |
1 |
1 |
|
0,25 |
|
||||||||||
|
2 |
|
13 |
|
|
15 |
-2 |
4 |
|
0,266667 |
|
||||||||||
|
3 |
|
36 |
|
|
40 |
-4 |
16 |
|
0,4 |
|
||||||||||
|
4 |
|
83 |
|
|
79 |
4 |
16 |
|
0,202532 |
|
||||||||||
|
5 |
|
101 |
|
|
97 |
4 |
16 |
|
0,164948 |
|
||||||||||
|
6 |
|
80 |
|
|
75 |
5 |
25 |
|
0,333333 |
|
||||||||||
|
7 |
|
35 |
|
|
33 |
2 |
4 |
|
0,121212 |
|
||||||||||
|
8 |
|
15 |
|
|
25 |
-10 |
100 |
|
4 |
|
||||||||||
|
Σ |
|
368 |
|
|
368 |
|
|
|
|
|
|
|
χн2 = 5,738692 |
|
||||||
Число степеней свободы, учитывая, что число групп выборки (число различных вариант) s = 8 , равно k = 8 −3 = 5 . По таблице приложения 5 находим χкр2 (0,05;5) =11,07048 .

83
Т.к. χн2 < χкр2 , то нет оснований отвергать нулевую гипотезу. Иными словами, расхо-
ждение эмпирических и теоретических частот незначимое. Т.о., данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
Этот пример легко выполняется с помощью Microsoft Excel. Наблюдаемое значение критерия:
χн2 =ХИ2ОБР(ХИ2ТЕСТ( ); s −1). Критическая же точка находится как
χкр2 (α;k) = ХИ2ОБР(α ; k ).
Сущность критерия согласия Пирсона состоит в сравнении эмпирических и теоретических частот. Понятно, что эмпирические частоты находят из опыта. Как найти теоретические частоты, если предполагается, что генеральная совокупность распределена нормально? Ниже приведен один из способов решения этой задачи.
1) Весь интервал наблюдаемых значений X (выборки объема n ) делят на s частичных интервалов одинаковой длины. Находят середины частичных интервалов xi* = (xi + xi+1 ) / 2 . В качестве частоты ni варианты xi* принимают число вариант, которые
попали в i -й интервал. В итоге имеют последовательность равноотстоящих вариант и соответствующих им частот:
Варианты xi* |
x1* |
x2* |
… |
xs* |
Эмпирические частоты ni |
n1 |
n2 |
… |
ns |
s
Естественно, что ∑ni = n .
i=1
2)Вычисляют выборочную среднюю x* и выборочное среднее квадратическое от-
клонение s* . |
|
|
|
3) Центрируют и нормируют случайную величину X , |
т.е. переходят к величине |
||
Z = ( X − x* ) / s* и вычисляют концы интервалов (zi ; zi+1 ) : |
|
|
|
zi = (xi − x* ) / s* , |
zi+1 = (xi+1 − x* ) / s* , |
|
|
причем наименьшее значение Z , т.е. z1 , полагают равным −∞, |
а наибольшее, т.е. zs , |
пола- |
|
гают равным + ∞. |
|
|
|
4) Вычисляют теоретические вероятности pi попадания случайной величины |
X в |
||
интервалы (xi ; xi+1 ) по формуле |
|
|
|
pi = Φ(zi+1 ) −Φ(zi ) ,
где Φ(z) – интегральная функция Лапласа (см. приложение 2). 5) Находят искомые теоретические частоты
ni′ = npi .
После применения описанного способа нахождения теоретических частот, естествен-
но, можно использовать то же правило проверки нулевой гипотезы. |
|
|
||||||||
|
ПримерU |
2.U Выборка объёма n =100 задана интервальным распределением: |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Интервал (xi ; xi+1 ) |
(0;10) |
(10;20) |
(20;30) |
(30;40) |
(40;50) |
|
||
|
|
Частота ni |
6 |
16 |
44 |
24 |
10 |
|
||
При уровне |
значимости α = 0,05 |
проверить гипотезу о нормальном распределении генераль- |
||||||||
ной совокупности.
Решение. Эмпирические частоты попадания в интервал заданы. Определим теоретические частоты, предполагая, что генеральная совокупность распределена нормально.
1) Весь интервал наблюдаемых значений X (выборки объема n =100 ) уже разделена на s = 5 частичных интервалов одинаковой длины. Найдём середины частичных интервалов
84
xi* . В качестве частоты ni варианты xi* примем число вариант, которые попали в i -й интер-
вал. В итоге имеют статистическое распределение равноотстоящих вариант и соответствующих им частот:
Варианта xi* |
5 |
15 |
25 |
35 |
45 |
Частота ni |
6 |
16 |
44 |
24 |
10 |
2)Выборочная средняя равна x* = 26,6 . Выборочное среднее квадратическое отклонение равно s* =10,072 .
3)Вычисляем концы интервалов (zi ; zi+1 ) (см. табл. 2).
|
|
|
|
|
Табл. 2. Нахождение концов интервалов |
||||
i |
Границы интервала |
|
|
Границы |
|
интервала |
|
||
xi |
xi+1 |
xi − x* |
xi+1 − x* |
zi = (xi − x* ) / s* |
|
zi+1 = (xi+1 − x* ) / s* |
|
||
1 |
0 |
10 |
|
-16,6 |
−∞ |
|
|
-1,64813 |
|
2 |
10 |
20 |
-16,6 |
-6,6 |
-1,64813 |
|
-0,65528 |
|
|
3 |
20 |
30 |
-6,6 |
3,4 |
-0,65528 |
|
0,337569 |
|
|
4 |
30 |
40 |
3,4 |
13,4 |
0,337569 |
|
1,330421 |
|
|
5 |
40 |
50 |
13,4 |
|
1,330421 |
|
|
+ ∞ |
|
4)Вычисляют теоретические вероятности pi (см. табл. 3).
5)Находим искомые теоретические частоты ni′ = npi (см. табл. 3).
Табл. 3. Нахождение теоретических вероятностей и частот
i |
Границы |
интервала |
Φ(zi ) |
Φ(zi+1 ) |
pi = Φ(zi+1 ) −Φ(zi ) |
ni′ = npi =100 pi |
zi |
zi+1 |
|||||
1 |
−∞ |
-1,64813 |
-0,5 |
-0,45034 |
0,049663 |
4,966263 |
2 |
-1,64813 |
-0,65528 |
-0,45034 |
-0,24386 |
0,20648 |
20,64804 |
3 |
-0,65528 |
0,337569 |
-0,24386 |
0,132156 |
0,376013 |
37,60131 |
4 |
0,337569 |
1,330421 |
0,132156 |
0,40831 |
0,276154 |
27,6154 |
5 |
1,330421 |
+ ∞ |
0,40831 |
0,5 |
0,09169 |
9,168987 |
|
|
|
|
|
s |
s |
|
|
|
|
|
∑pi =1 |
∑ni′ =100 |
|
|
|
|
|
i=1 |
i=1 |
Вычисления необходимые для определения наблюдаемого значения критерия приведём в табл. 4.
|
|
Табл. 4. |
Расчёт наблюдаемого значения критерия Пирсона |
||||||
i |
ni |
ni′ |
ni −ni′ |
(n −n′)2 |
|
(n −n′)2 |
|
||
|
|
|
|
i i |
|
i |
i |
|
|
|
|
|
|
|
|
|
ni′ |
|
|
1 |
6 |
4,966263 |
1,033737 |
1,068612 |
|
|
0,215174 |
|
|
2 |
16 |
20,64804 |
-4,64804 21,60429 |
|
|
1,046312 |
|
||
3 |
44 |
37,60131 |
6,398692 |
40,94326 |
|
|
1,088879 |
|
|
4 |
24 |
27,6154 |
-3,6154 |
13,07113 |
|
|
0,473327 |
|
|
5 |
10 |
9,168987 |
0,831013 |
0,690583 |
|
|
0,075317 |
|
|
Σ |
100 |
100 |
|
|
|
χн2 |
= 2,89901 |
|
|
85
Число степеней свободы, учитывая, что число групп выборки s = 5 , равно k = 5 −3 = 2 . По таблице приложения 5 находим χкр2 (0,05;2) = 5,991476 .
Т.к. χн2 < χкр2 , то нет оснований отвергать нулевую гипотезу. Иными словами, расхо-
ждение эмпирических и теоретических частот незначимое. Т.о., данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.

86
Лекция 8. ОБЩИЕU ПОНЯТИЯ О КОРРЕЛЯЦИИ И РЕГРЕССИИ U
План
1.Виды связи между случайными величинами. Числовые характеристики системы
двух случайных величин.
2.Выборочное уравнение регрессии. Сглаживание экспериментальных зависимо-
стей методом наименьших квадратов (МНК).
3.Выборочное уравнение прямой линии регрессии.
1.Рассмотрим практический опыт, целью которого является исследование зависимости некоторой случайной величины Y от другой случайной величины X . Например, зависимость урожайности зерновых культур от количества вносимых удобрений; зависимость себестоимости продукции от производительности труда; зависимость начальной скорости снаряда от температуры порохового заряда и т.д. Случайные величины могут быть связаны либо функциональной зависимостью, либо статистической, либо быть независимыми.
Строгая функциональная зависимость между случайными величинами присутствует редко. Это связано с тем, что обе величины или одна из них подвержены действию случайных факторов. Более того, среди этих факторов могут быть и общие, т.е. воздействующие и на Y , и на X .
Статистической (стохастической, вероятностной) называют зависимость, при ко-
торой изменение одной из величин влечет изменение закона распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой. В этом случае статистическую зависимость называют корреляционной. Задачи изучения зависимостей между величинами, связь между которыми не является строго функциональной, решаются в рамках т.н. теории корреляции.
Для проведения четких аналогий между понятиями теории вероятностей и математической статистики приведём некоторые определения и факты.
Условным математическим ожиданием (условной средней) y(x) (или yx ) дискрет-
ной случайной величины Y при X = x ( x – конкретное возможное значение X ) называют:
n
M (Y / x) = M (Y / X = x) = ∑yi p( yi / x) = y(x) .
i=1
Для непрерывных случайных величин:
M (Y / x) = M (Y / X = x) = +∞∫yf ( y / x)dy = y(x) ,
−∞
где f ( y / x) – условная плотность случайной величины Y при X = x . Условное математическое ожидание M (Y / x) есть функция от x :
M (Y / x) = y(x) ,
которую называют функцией регрессии Y на X (или, Y по X ). График функции y = y(x)
называют линией регрессии Y на X . В случае непрерывного распределения, действительно, будет «линия» в обычном понимании этого слова. В дискретном случае – будем иметь некоторое множество изолированных точек на плоскости. Аналогично определяется функция регрессии X на Y :
M ( X / y) = x( y) .
2. Условное среднее yx является функцией от х, поэтому, обозначив эту функцию через ϕ(х) , получим уравнение
yx =ϕ(х) .
87
Это уравнение называют выборочным уравнением регрессии Y на X . Сама функция ϕ(х)
называется выборочной регрессией Y на X , а ее график – выборочной линией регрессии Y на
X .
Пусть изучается система количественных признаков ( X ;Y ), которые представлены экспериментальными данными в табл. 1:
Табл. 1. Статистические данные двух количественных признаков
xi |
x1 |
x2 |
… |
xn |
yi |
y1 |
y2 |
… |
yn |
Предположим, что между количественными признаками имеется количественная связь: y =ϕ(х) .
Одними из главных задач математической статистики являются:
•определение вида связи ϕ(х) ;
•выяснение вопроса тесноты связи и коррелированности величин X и Y .
Первую задачу обычно называют задачей сглаживания экспериментальной зависимости. Желательно так обработать данные опыта, чтобы по возможности точно отразить общую тенденцию зависимости y от x , и вместе с тем сгладить незакономерные, случайные откло-
нения, связанные с погрешностями самого наблюдения.
Как уже говорилось, для подобных задач обычно применяют метод наименьших квадратов (МНК). Этот метод дает возможность при заданном типе зависимости y =ϕ(х)
(например, y = aх+b ) так выбрать ее числовые параметры (т.е. a и b ), чтобы кривая y =ϕ(х) в определенном смысле наилучшим образом отображала экспериментальные данные. При использовании МНК требование наилучшего согласования кривой y =ϕ(х) и экс-
периментальных точек сводится к тому, чтобы сумма квадратов отклонений эксперимен-
тальных точек от сглаживающей кривой была минимальной:
n
∑[ yi −ϕ(xi )]2 → min .
i=1
Из каких же соображений выбирают тип кривой y =ϕ(х) ? Часто этот вопрос решается следующим образом: на график наносятся статистические данные в виде точек с координатами (xi ; yi ), i =1,2,..., n . Совокупность этих точек в системе координат называют корреляционным полем. Тип функции ϕ определяется по внешнему виду экспериментальной зави-
симости. Часто же бывает так, что физические или другие особенности опыта подсказывают тип кривой y =ϕ(х) .
Перейдем к задаче определения параметров a,b,c,... , исходя из принципа наименьших
квадратов. Пусть имеется таблица экспериментальных данных (табл. 1) и пусть из каких-то соображений выбран общий вид функции y =ϕ(х) , зависящей от нескольких числовых па-
раметров a,b,c,... . Именно эти параметры и требуется выбрать согласно МНК так, чтобы сумма квадратов отклонений yi от ϕ(xi ) была минимальной. Запишем y как функцию не только аргумента x , но и параметров a,b,c,... :
y =ϕ(x;a,b,c,...) .
Требуется выбрать a,b,c,... так, чтобы выполнялось условие
n
∑[ yi −ϕ(xi ;a,b,c,...)]2 → min .
i=1
Для этого продифференцируем функцию выборочной регрессии ее по a,b,c,... и приравняем производные к нулю. Полученная система будет содержать столько же уравнений, сколько и

88
неизвестных a,b,c,... . Для того, чтобы её решить, необходимо задать конкретный вид функции ϕ .
3. Рассмотрим часто встречающийся на практике случай: когда предполагаемая зависимость линейна, т.е. функция связи ищется в виде
y = ϕ(x; a,b) = ax +b .
Составляем общую систему уравнений для нахождения параметров a и b :
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑[ yi − (axi + b)]xi = 0, |
|
|
|||||||||||||||||||
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑[ yi − (axi + b)] = 0. |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Раскроем скобки, произведём суммирование и разделим оба уравнения на n : |
|||||||||||||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|||
|
|
|
|
∑xi yi |
|
|
|
|
∑xi |
2 |
|
|
|
∑xi |
|
|
|
|
|
||||||||
|
|
|
|
|
i=1 |
|
|
|
− a |
i=1 |
|
|
|
−b |
i=1 |
|
= 0, |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
∑yi |
|
|
|
∑xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
i=1 |
|
− a |
i=1 |
|
−b = 0. |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Суммы, входящие в уравнения системы, представляют собой статистические моменты: |
|||||||||||||||||||||||||||
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
∑xi |
= a |
( X ) = x, |
∑yi |
|
|
|
|
|
|
|
|
|
∑xi |
2 |
|
|
|
|
∑xi yi |
|
||||||
|
i=1 |
i=1 |
|
= a |
(Y ) = y, |
|
i=1 |
|
|
= a |
2 |
( X ), |
i=1 |
|
= a ( X ,Y ) . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
n |
1 |
|
n |
|
|
1 |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
1,1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следовательно, наша система примет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
a |
( X |
,Y ) −a a |
|
( X ) −bx = 0, |
|
|
|||||||||||||||||
|
|
|
|
1,1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
y −ax −b = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Выразим b из второго уравнения системы и подставим в первое. В итоге получим |
|||||||||||||||||||||||||||
|
|
|
b = y −ax, |
a = |
a1,1 ( X ,Y ) − x y |
= |
m1,1 ( X ,Y ) |
, |
|
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a2 ( X ) −(x)2 |
|
sX 2 |
|
|
|||||||||||
где m1,1 ( X ,Y ) – выборочная ковариация (или выборочный корреляционный момент, или вы-
борочный совместный момент первого порядка), sX |
2 – выборочная дисперсия. |
||||||
Т.о., линейная зависимость, связывающая y и x , имеет вид: |
|||||||
y = |
m1,1 ( X ,Y ) |
x + y − |
m1,1 ( X ,Y ) |
x . |
|||
|
|
||||||
|
sX |
2 |
|
|
sX |
2 |
|
Напомним, что нашей задачей было нахождение выборочным уравнением регрессии Y на |
|||||||
X : |
yx |
= aх+b . |
|
|
|
||
|
|
|
|
|
|||
Поэтому, несколько перегруппировав уравнение линейной связи, получим уравнение прямой линии регрессии Y на X :
yx − y = m1,1s(XX2 ,Y ) (x − x) .
Если же ввести в рассмотрение выборочный коэффициент корреляции
rB = m1,1 ( X ,Y ) , sX sY
то уравнение прямой линии регрессии Y на X примет вид

89
y |
|
− y = r |
sY |
(x − x) . |
|
|
|||
|
x |
B sX |
||
Можно отметить, что данная прямая проходит через точку (x; y) и её угловой коэффициент
равен |
r |
|
sY |
. Общий результат можно сформулировать в виде следующего утверждения. |
|||||||||||
|
|
||||||||||||||
|
B sX |
|
.U Уравнение прямой линии регрессии Y на X имеет вид: |
||||||||||||
|
УтверждениеU |
||||||||||||||
|
|
|
|
|
|
|
|
|
y |
|
− y = r |
sY |
(x − x) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
x |
B sX |
|
|||
|
|
1 |
n |
|
1 |
n |
|
n |
|
|
|
n |
|||
где x = |
∑xi |
, y = |
∑yi , sX = |
1 ∑( xi − x )2 , sY = |
1 ∑( yi − y)2 . Здесь rB – выбороч- |
||||||||||
n |
|
||||||||||||||
|
|
i=1 |
|
n i=1 |
n |
i=1 |
n i=1 |
||||||||
ный коэффициент корреляции, который вычисляется по формуле:
|
|
1 |
∑∑nxy (x − x)( y − y) |
|
|
|
n |
||
r |
= |
x y |
||
|
|
|||
B |
sX sY |
|||
|
|
|
|
|
|
1 |
∑∑nxy xy − x y ∑∑nxy xy −n x y |
||||||
|
n |
|||||||
= |
x y |
|
= |
x y |
|
, |
||
|
|
|
|
|
||||
|
|
|
|
sX sY |
n sX sY |
|||
где x , y – варианты (наблюдавшиеся значения) случайных величин X , Y ; nxy – частота пары вариант (x, y) , n – объём выборки.
Коэффициент ρ |
|
= r |
sY |
называют выборочным коэффициентом регрессии Y на X . |
|||||||||
|
|
||||||||||||
|
YX |
B sX |
|
|
|
|
|
|
|
|
|
||
Уравнение прямой регрессии Y на X можно записать в виде: |
|
|
|
|
|||||||||
|
|
|
|
|
yx − y = ρYX (x − x) . |
|
|
|
|
||||
Несколько преобразовав последнее уравнение, получим |
|
|
|
|
|||||||||
|
|
|
|
yx = ρYX x + y − ρYX x . |
|
|
|
|
|||||
Уравнение прямой линии регрессии X на Y имеет вид: |
|
|
|
|
|||||||||
|
|
|
|
x |
|
− x = r |
sX |
( y − y) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
y |
|
B |
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
sX |
|
|
Вводя выборочный коэффициент регрессии |
X на Y , а именно ρ |
|
= r |
, получим |
|||||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
XY |
B |
sY |
|
xy − x = ρXY ( y − y) .

90
Лекция 9. НАХОЖДЕНИЕU УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ РЕГРЕССИИ U
План
1.Выборочный коэффициент корреляции. Проверка гипотезы о значимости выборочного коэффициента корреляции.
2.Практические способы решения задач линейной регрессии.
1.Поговорим теперь подробно о выборочном коэффициенте корреляции rB . Он является статистическим аналогом для коэффициента корреляции rXY , который вводился в курсе теории вероятностей. Коэффициент корреляции rXY характеризует не всякую зависимость, а
только линейную. Линейная вероятностная зависимость случайных величин заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать (или же убывать) по линейному закону. Коэффициент корреляции характеризует степень тесноты линейной зависимости между случайными величинами. Если случайные величины X и Y связаны точной линейной функциональной зависимостью:
Y = aX + b ,
то rXY = ±1. Знак «плюс» или «минус» берется в зависимости от того, положителен или отрицателен коэффициент a . Вернёмся к задачам математической статистики и будем говорить о выборочном коэффициенте корреляции rB . В общем случае, когда величины X и Y связаны
произвольной статистической зависимостью, этот коэффициент находится в пределах:
−1 < rB <1.
В случае rB > 0 говорят о положительной выборочной корреляции величин X и Y , в случае rB < 0 – об отрицательной корреляции. Положительная корреляция между случайными ве-
личинами означает, что при возрастании одной из них другая имеет тенденцию в среднем возрастать. Отрицательная корреляция означает, что при возрастании одной из случайных величин другая имеет тенденцию в среднем убывать. Например, а) вес и рост человека связаны положительной корреляцией; б) время, потраченное на регулировку прибора при подготовке к его работе, и время его безотказной работы связаны положительной корреляцией; в) наоборот, время, потраченное на подготовку, и количество неисправностей, обнаруженное при работе прибора, связаны отрицательной корреляцией.
Выборочный коэффициент корреляции rB является оценкой коэффициента корреляции rXY генеральной совокупности. Допустим, что в ходе эксперимента или измерений rB
оказался отличным от нуля. Т.к. выборка отобрана случайно, то нельзя делать вывод о том, что rXY также отличен от нуля. Необходимо проверить гипотезу о значимости (существенно-
сти) выборочного коэффициента корреляции rB , или, что то же самое, гипотезу о равенстве нулю коэффициента корреляции генеральной совокупности rXY . Если гипотеза о равенстве нулю коэффициента корреляции генеральной совокупности rXY будет отвергнута, то выборочный коэффициент корреляции rB значим, а величины X и Y коррелированы. В против-
ном случае он незначим, а величины X и Y некоррелированы.
Рассмотрим случай двумерной нормально распределённой генеральной совокупности ( X ,Y ) . Из совокупности извлечена выборка объёма n и по ней вычислен выборочный коэф-
фициент корреляции rB ≠ 0 . Требуется проверить нулевую гипотезу H 0 : rXY = 0 при конкурирующей гипотезе H1 : rXY ≠ 0 . Для этой цели вычисляют наблюдаемое значение критерия
Тн = rB1−nr−B 22 .

91
Используя таблицу критических точек распределения Стьюдента, по заданному уровню значимости α и числу степеней свободы k = n −2 , находят критическую точку tкр (α;k) двухс-
торонней критической области. Если оказывается, что Тн < tкр , то нет нет оснований отвергать нулевую гипотезу. В противном же случае её отвергают.
2. Приведем пример, позволяющий судить о задачах линейной регрессии.
ПримерU 1.U По выборочным данным для случайных величин X и Y (табл. 1) требуется
найти:
1)основные числовые характеристики выборки (выборочное среднее, дисперсию, среднее квадратическое отклонение);
2)характеристики взаимовлияния случайных величин (выборочную ковариацию, выборочный коэффициент корреляции) и объяснить степень тесноты линейной связи;
3)проверить значимость коэффициента корреляции с помощью критерия Стьюдента при уровне значимости α = 0,05 ;
4)выборочное уравнение линейной регрессии Y на X , объяснить его, построить корреляционное поле и прямую выборочной регрессии в нем.
Табл. 1. Данные задачи: X – средняя месячная доходность (%) фондового индекса, Y – средняя месячная доходность (%) акции корпорации “Омега”
|
X |
|
5,3 |
19 |
21 |
|
|
2,8 |
-8,9 |
2,8 |
-14 |
-5,3 |
-3 |
11 |
|
|
|
Y |
|
-3 |
8,2 |
6,1 |
|
|
-0,3 |
-4 |
-0,3 |
-4,8 |
-1,4 |
-5 |
-2 |
|
|
Решение. |
|
|
|
1 |
n |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1) Выборочное среднее: x = |
∑xi , где xi |
( i =1,2,..., n ) – наблюдаемые значения слу- |
||||||||||||||
n |
||||||||||||||||
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|||
чайной величины X , вошедшие в выборку объема n . В нашей задаче n =10 . Вычисляем: x = 101 (5,3 +19,0 +... +11,0) = 3,07 ; y = −0,65 .
Дисперсия выборки (выборочная дисперсия) sX 2 вычисляется по формулам:
|
1 |
n |
1 |
n |
sX 2 = |
∑(xi − x )2 = |
∑xi 2 −(x )2 . |
||
|
n |
i=1 |
n i=1 |
|
Выборочное среднее квадратическое (стандартное) отклонение sX – это квадратный корень
из выборочной дисперсии sX |
2 . |
|
|
|
||
Находим дисперсии и стандартные отклонения обеих выборок: |
||||||
sX 2 = |
1 |
(5,3)2 +(19,0)2 |
+... +(11,0)2 −(3,07)2 |
=118,4821; sX = 118, 4821 =10,8850 ; |
||
|
||||||
10 |
s 2 |
|
s |
|
||
|
|
|
=17,9405 ; |
= 4,2356 . |
||
|
|
|
Y |
|
Y |
|
2) Найдем характеристики взаимовлияния случайных величин – выборочную ковариацию, выборочный коэффициент корреляции, и объясним степень тесноты линейной связи.
Выборочной ковариацией называют число:
|
|
|
|
n |
|
n |
|
|
|
|
covB ( X ,Y ) = |
1 ∑(xi |
− x)( yi − y) = |
1 ∑xi yi − x y . |
|
Вычисляя его, получим |
n i=1 |
|
n i=1 |
||||
|
|
|
|||||
covB (X ,Y ) = |
|
1 |
[5,3 (−3,0) +19,0 8,2 +... +11,0 (−2,0)]−3,07 (−0,65) = 38,9495 . |
||||
10 |
|||||||
|
|
|
|
|
|||
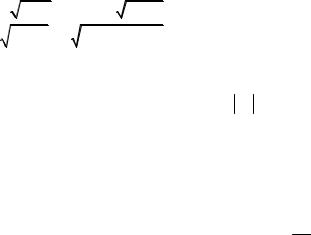
|
|
|
|
|
|
|
|
|
|
|
|
|
92 |
|
Выборочный коэффициент корреляции |
|
|
рассчитывается следующим |
образом: |
||||||||
rB = |
covB ( X ,Y ) |
. Подставив числовые |
значения, имеем rB = 0,8448 . |
Судя |
по знаку |
||||||||
sX sY |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rB = 0,8448 , корреляция между X и Y |
– положительная (т.е. при увеличении величины X |
||||||||||||
величина Y |
в среднем увеличивается). |
А т.к. |
|
rB |
|
|
≈1 , то связь между X |
и Y |
достаточно |
||||
|
|
||||||||||||
близка к линейной. |
|
|
|
|
|
|
|
|
|||||
|
3) Вычислим наблюдаемое значение критерия Стьюдента: |
|
|
||||||||||
|
|
|
Тн = |
rB n −2 |
= 0,8448 |
10 −2 ≈ 4, 4656 . |
|
|
|||||
|
|
|
|
|
|
||||||||
|
|
|
|
1−r 2 |
1−(0,8448)2 |
|
|
||||||
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
Используя таблицу критических точек распределения Стьюдента, по заданному уровню значимости α = 0,05 и числу степеней свободы k = n −2 =10 −2 = 8 , найдём критическую точку
двухсторонней критической области tкр (0,05;8) = 2,306006 . Т.к. Тн > tкр , то гипотеза о равенстве нулю генерального коэффициента корреляции rXY отвергается. Т.е. коэффициент
корреляции значимо отличается от нуля и, следовательно, X и Y коррелированы. Коротко говоря, коэффициент корреляции значим с надежностью не менее 95%
4) Найдем выборочное уравнение линейной регрессии Y на X , объясним его, построим корреляционное поле и прямую выборочной регрессии в нем.
Уравнение прямой линии регрессии Y на X имеет вид: y − y = rB sY (x − x) . Можно sX
отметить, что данная прямая проходит через точку (x; y) . Угловой коэффициент этой пря-
мой ρ |
|
= r |
sY |
называют выборочным коэффициентом регрессии Y на X . Уравнение пря- |
|
|
|||
|
YX |
B sX |
||
мой регрессии Y на X можно записать в виде: y − y = ρYX (x − x) . Несколько преобразовав последнее уравнение, получим: y = ρYX x + y − ρYX x . Подставив численные значения, имеем y = 0,3287x −1,6592 .
Т.о., с увеличением величины X на 1 единицу величина Y увеличивается в среднем на 0,3287 единицы. Непосредственно для нашей задачи – при увеличении доходности фондового индекса на 1% доходность акции в среднем вырастет на 0,3287%.
Корреляционное поле и линия регрессии на нем выглядит так:
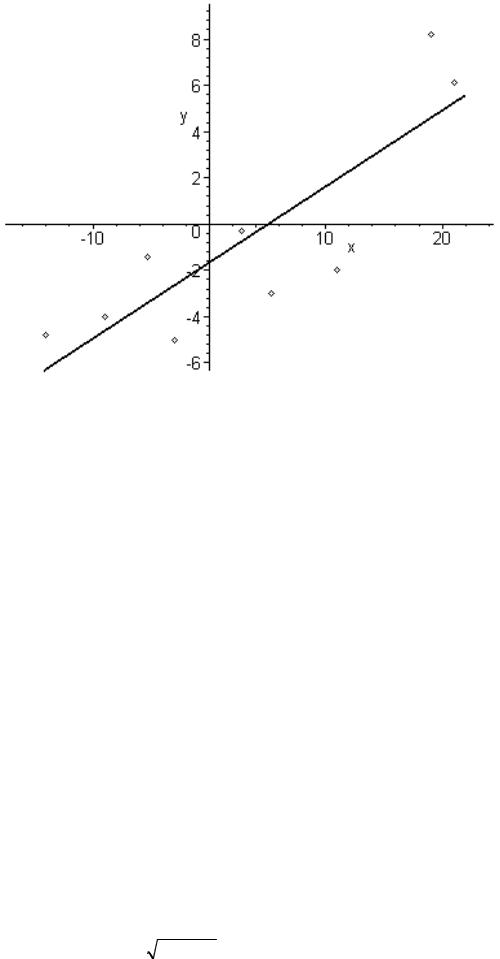
93
ЗамечаниеU .U Практически любой пакет прикладных программ, позволяющий делать математические расчеты, содержит статистические функции или процедуры. Например, в Microsoft Excel встроены статистические функции, среди которых есть СРЗНАЧ( ), ДИСП( ), СТАНДОТКЛОН( ), КОВАР( ), КОРРЕЛ( ) и т.д. Весьма хорош математический пакет Maple (любой версии).
Для того, чтобы выполнить подобную задачу без использования компьютера, удобно пользоваться табл. 2.
Табл. 2. Расчеты к задаче на парную корреляцию
№ |
xi |
|
yi |
|
x 2 |
y 2 |
xi yi |
|
|
|
|
|
i |
i |
|
1 |
|
5,3 |
|
-3 |
28,09 |
9 |
-15,9 |
2 |
|
19 |
|
8,2 |
361 |
67,24 |
155,8 |
3 |
|
21 |
|
6,1 |
441 |
37,21 |
128,1 |
4 |
|
2,8 |
|
-0,3 |
7,84 |
0,09 |
-0,84 |
5 |
|
-8,9 |
|
-4 |
79,21 |
16 |
35,6 |
6 |
|
2,8 |
|
-0,3 |
7,84 |
0,09 |
-0,84 |
7 |
|
-14 |
|
-4,8 |
196 |
23,04 |
67,2 |
8 |
|
-5,3 |
|
-1,4 |
28,09 |
1,96 |
7,42 |
9 |
|
-3 |
|
-5 |
9 |
25 |
15 |
10 |
|
11 |
|
-2 |
121 |
4 |
-22 |
Σ |
|
30,7 |
|
-6,5 |
1279,07 |
183,63 |
369,54 |
В нашей задаче n =10 , поэтому получим: |
|
−6,5 |
|
||
x = |
30,7 |
= 3,07 ; |
y = |
= −0,65 ; |
|
|
10 |
|
|
10 |
|
s |
2 |
= 1279,07 −(3,07)2 |
=118, 4821; |
s 2 |
= 183,63 −(−0,65)2 =17,9405 ; |
|
X |
10 |
|
Y |
10 |
|
|
|
|
||
|
|
sX = |
118, 4821 =10,8850 ; |
sY = 4,2356 . |
|
94
Для расчета выборочной ковариации воспользуемся последним столбцом табл. 2: covB ( X ,Y ) = 369,5410 −3,07 (−0,65) = 38,9495 ,
откуда
|
|
|
|
|
|
|
|
rB = |
38,9495 |
= 0,8448 . |
|
|
|
|
|
|
|
|
|
10,8850 |
4,2356 |
||
|
|
|
|
|
|
|
|
|
|
||
|
Эконометрическую модель мы ищем в виде: |
|
|||||||||
|
|
|
|
sY |
|
|
|
|
y = a0 + a1 x , |
||
где a |
= ρ |
|
= r |
, a |
= y − ρ |
|
x . Подставляя численные значения, получим |
||||
|
|
|
|||||||||
1 |
|
YX |
B sX |
0 |
|
YX |
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 = 0,3287 , |
a0 = −1,6592 . |
||
В итоге, имеем
y = −1,6592 +0,3287x .

95
Лекция 10. НАХОЖДЕНИЕU УРАВНЕНИЙ КРИВОЛИНЕЙНОЙ РЕГРЕССИИ U
План
1.Параболическая корреляция второго порядка.
2.Методы нахождения уравнений криволинейной регрессии.
3.Понятие о множественной корреляции.
1. Рассмотрим задачу нахождения уравнения регрессии yx =ϕ(х) (или xy =ψ( y) ) между данными эксперимента (или измерений) x1 , x2 ,..., xn и y1 , y2 ,..., yn . Наиболее приме-
ним для этой цели МНК. Для его использования необходимо задать конкретный вид функции ϕ (или ψ ). Если график линии регресии изображается кривой линией, то корреляцию
называют криволинейной. Напомним, что тип функции ϕ определяется либо по внешнему
виду экспериментальной зависимости (т.е. фактически по виду корреляционного поля), либо по физическим или другим особенностями опыта.
Часто встречающийся на практике случай: когда функция ϕ выражается многочленом (полиномом) второй степени – параболой второго порядка:
ϕ(x;a,b,c) = ax2 +bx +c .
Этот случай принято называть параболической корреляцией второго порядка.
Согласно МНК требуется выбрать параметры a,b,c так, чтобы выполнялось условие
n
∑[ yi −ϕ(xi ;a,b,c)]2 → min .
i=1
Соответствующая система уравнений примет вид:
n |
|
|
|
|
|
2 = 0, |
∑[ yi −(axi2 +bxi +c)]xi |
||||||
i=1 |
|
|
|
|
|
|
n |
[ y |
−(ax2 +bx |
|
+c)]x |
|
= 0, |
|
|
|
||||
|
i |
i |
|
i |
|
|
∑ i |
|
|
||||
i=1 |
|
|
|
|
|
|
n
∑[ yi −(axi2 +bxi +c)] = 0.
i=1
Если раскрыть скобки, просуммировать и разделить на n , то получим следующую систему уравнений:
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|||
|
∑xi2 yi |
|
|
|
∑xi4 |
|
|
|
|
∑xi3 |
|
|
∑xi2 |
|
|
|||||||||
i=1 |
|
|
−a |
|
i=1 |
|
|
−b |
|
i=1 |
|
|
−c |
|
i=1 |
|
= 0, |
|||||||
|
n |
|
|
|
n |
|
|
|
n |
|
|
|
n |
|
||||||||||
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|||
|
∑xi yi |
|
|
∑xi3 |
|
|
∑xi2 |
|
∑xi |
|
|
|||||||||||||
|
i=1 |
|
|
−a |
|
i=1 |
|
|
−b |
i=1 |
|
|
−c |
|
i=1 |
|
= 0, |
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
n |
|
|
|
n |
|
|
|
|
|
|
|
n |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
||||||
|
n |
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
∑yi |
|
|
|
∑xi2 |
|
|
|
∑xi |
|
|
|
|
|
|
|
|
|||||||
i=1 |
−a |
i=1 |
−b |
i=1 |
−c = 0. |
|
|
|||||||||||||||||
|
n |
|
n |
|
|
|
n |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Суммы, входящие в уравнения системы, представляют собой статистические моменты системы двух случайных величин X , Y , а именно:

96
|
n |
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
||
|
∑xi |
= a |
( X ) = x, |
∑yi |
= a |
(Y ) = y, |
∑xi |
2 |
= a |
|
|
(X ), |
∑xi |
3 |
= a |
|
( X ), |
∑xi |
4 |
= a |
|
(X ) , |
|||||||
|
i=1 |
i=1 |
|
i=1 |
|
|
2 |
i=1 |
|
3 |
i=1 |
|
4 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
n |
1 |
|
n |
|
|
1 |
|
|
n |
|
|
|
|
|
n |
|
|
|
n |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑xi yi |
|
∑xi |
2 yi |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
i=1 |
|
|
|
|
= a1,1 (X ,Y ), |
|
i=1 |
|
|
|
= a2,1 ( X ,Y ) . |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, наша система примет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
a4 (X )a + a3 ( X )b + a2 (X )c = a2,1 (X ,Y ), |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
( X )a + a2 ( X )b + a1 (X )c = a1,1 (X ,Y ), |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
a3 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
a |
2 |
(X )a + a (X )b + |
1 c = a (Y ). |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
Это система 3-х линейных уравнений с тремя неизвестными a,b,c , которые можно найти,
используя какой-то из методов линейной алгебры (например, метод Гаусса).
ЗамечаниеU 1.U Если данные эксперимента сгруппированы в корреляционную таблицу, то вместо последней системы удобнее пользоваться системой вида
|
|
|
|
|
|
|
∑x4 nx a |
|
|
x |
|
|
|
|
|
|
|
|
∑x3nx a |
|
|
x |
|
|
|
|
|
∑x2 nx a |
|
|
x |
|
|
|
|
|
∑x3nx |
|
|
∑x2 nx |
|
|
|
|
|
||
+ |
b + |
c = |
|
∑yx x2 nx , |
|||||||
|
x |
|
|
|
x |
|
|
|
|
x |
|
|
∑x2 nx |
|
|
|
|
|
|
∑yx xnx |
|
||
+ |
b + |
∑xnx c |
= |
, |
|||||||
|
x |
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
∑xnx b + nc = |
∑yx nx . |
|
|
|||||||
|
x |
|
|
|
|
x |
|
|
|
|
|
ПримерU 1.U Найти выборочное уравнение регрессии Y на X вида yx = ax2 +bx +c по данным корреляционной табл. 1.
Табл. 1. Корреляционная таблица к примеру 1
Y |
|
|
X |
|
ny |
1 |
2 |
3 |
4 |
||
|
|
|
|
|
|
5 |
3 |
1 |
|
|
4 |
15 |
1 |
4 |
2 |
|
7 |
40 |
|
1 |
9 |
1 |
11 |
65 |
|
|
2 |
6 |
8 |
nx |
4 |
6 |
13 |
7 |
n = 30 |
yx |
7,5 |
17,5 |
40 |
61,4286 |
|
Решение. Представим несколько способов решения: а) без использования программных средств; б) с помощью компьютера.
а) Составим расчётную табл. 2:
Табл. 2. Расчёты по параболической корреляции второго порядка
x |
nx |
yx |
xnx |
x2 nx |
x3nx |
x4 nx |
yx nx |
yx xnx |
yx x2 nx |
1 |
4 |
7,5 |
4 |
4 |
4 |
4 |
30 |
30 |
30 |
2 |
6 |
17,5 |
12 |
24 |
48 |
96 |
105 |
210 |
420 |
3 |
13 |
40 |
39 |
117 |
351 |
1053 |
520 |
1560 |
4680 |
4 |
7 |
61,4286 |
28 |
112 |
448 |
1792 |
430 |
1720 |
6880 |
Σ |
30 |
— |
83 |
257 |
851 |
2945 |
1085 |
3520 |
12010 |

97
На основании расчётов табл. 2 составим систему уравнеий:
2945a +851b + 257c =12010,851a + 257b +83c = 3520,257a +83b +30c =1085.
Решив эту систему, получим: a ≈ 2,3632; b ≈ 6,8478; c ≈ −3,0234 . Искомое уравнение регресии:
yx = 2,3632x2 +6,8478x −3,0234 .
б) Для того, чтобы решить ту же задачу в Microsoft Excel, нужно выполнить следующую последовательность действий:
•ввести экспериментальные данные постолбцово (или построчно);
•на основании введённых данных построить точечную диаграмму;
•активизировать данные диаграммы, щёлкнув по точкам правой кнопкой «мыши»;
•в пункте меню «Диаграмма» выбрать опцию «Добавить линию тренда…»;
•в пункте меню «Тип» выбрать «Полиномиальная (степень 2)» и в пункте «Параметры» – «Показывать уравнение на диаграмме».
Результаты решения нашей задачи присутствуют на рис. 1. Обратим внимание на то,
что уравнение регрессии совпало с уравнением, найденным способом а). |
|
|||||
|
|
Параболическая корреляция второго порядка |
|
|||
|
70 |
|
y = 2,3632x2 |
+ 6,8478x - 3,0234 |
|
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
50 |
|
|
|
|
|
y |
40 |
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
x |
|
|
|
|
Рис. 1. Решение примера 1 с помощью Microsoft Excel |
|
|||
Случай параболической корреляции рассмотрен полностью.
2. Не очень сложно решается задача сглаживания экспериментальной зависимости методом наименьших квадратов и в том случае, когда уравнение регресии представляет собой не многочлен, а сумму произвольных заданных функций ϕ1 (x),ϕ2 (x),...,ϕk (x) c коэффи-
циентами a1 , a2 ,..., ak , которые подлежат определению:
k
yx =ϕ(x;a1, a2 ,..., ak ) = a1ϕ1 (x) + a2ϕ2 (x) +... + akϕk (x) = ∑aiϕi (x) .
i=1
Удобно сглаживать экспериментальную зависимость, например, тригонометрическим многочленом
ϕ(x;a1 , a2 , a3 , a4 ) = a1 cosωx + a2 sinωx + a3 cos 2ωx + a4 sin 2ωx
или линейной комбинацией экспоненциальных функций
ϕ(x;a1 , a2 , a3 ) = a1eαt + a2eβt + a3eγt .
98
В общем случае задача нахождения коэффициентов a1 , a2 ,..., ak сводится к решению системы k линейных уравнений
|
n |
|
−[a1ϕ1 |
(xi ) + a2ϕ2 |
(xi ) +... + akϕk (xi )])ϕ1 (xi ) = 0, |
|||
∑( yi |
||||||||
i=1 |
|
|
|
|
|
|
|
|
|
n |
( y −[a ϕ (x ) + a ϕ (x ) +... + a ϕ (x )])ϕ (x ) = 0, |
||||||
|
|
|||||||
∑ i |
1 1 |
i |
2 2 |
i |
k k i |
2 i |
||
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
−[a1ϕ1 |
(xi ) + a2ϕ2 |
(xi ) +... + akϕk (xi )])ϕk (xi ) = 0. |
|||
∑( yi |
||||||||
i=1 |
|
|
|
|
|
|
|
|
Суммируя почленно, получим
|
n |
n |
|
n |
n |
a1 |
∑[ϕ1 (xi )]2 + a2 |
∑ϕ2 (xi )ϕ1 (xi ) +... + ak ∑ϕk (xi )ϕ1 (xi ) = ∑yiϕ1 (xi ), |
|||
i=1 |
i=1 |
|
i=1 |
i=1 |
|
|
n |
|
n |
n |
n |
a1 |
∑ϕ1 (xi )ϕ2 (xi ) + a2 |
∑[ϕ2 (xi )]2 +... + ak ∑ϕk (xi )ϕ2 (xi ) = ∑yiϕ2 (xi ), |
|||
|
i=1 |
|
i=1 |
i=1 |
i=1 |
|
|
|
|
|
|
|
n |
|
n |
n |
n |
|
|
||||
a1 |
∑ϕ1 (xi )ϕk (xi ) + a2 |
∑ϕ2 (xi )ϕk (xi ) +... + ak ∑[ϕk (xi )]2 |
= ∑yiϕk (xi ). |
||
|
i=1 |
|
i=1 |
i=1 |
i=1 |
Записывая последнюю систему более компактно, приходим к окончательному виду
|
k |
n |
∑a j ∑ϕ1 |
||
j=1 |
i=1 |
|
|
k |
n |
∑a j ∑ϕ2 |
||
j=1 |
i=1 |
|
|
|
|
|
|
|
|
k |
n |
∑a j ∑ϕk |
||
j=1 |
i=1 |
|
n
(xi )ϕ j (xi ) = ∑yiϕ1 (xi ),
i=1
n
(xi )ϕ j (xi ) = ∑yiϕ2 (xi ),
i=1
n
(xi )ϕ j (xi ) = ∑yiϕk (xi ).
i=1
Решая эту систему линейных уравнений, мы всегда найдём коэффициенты a1 , a2 ,..., ak . Несколько сложнее находить уравнение криволинейной регрессии yx =ϕ(x;a,b,c,...) ,
если параметры a,b,c,... входят в него нелинейно, т.е. yx = aebx , yx = axb и т.д. Если выпи-
сывать системы уравнений, соответствующие методу наименьших квадратов, то их решение может оказаться достаточно трудоёмким. Однако эту сложность можно преодолеть, если использовать специальные приёмы или применить программные средства.
При использовании Microsoft Excel, нужно выполнять последовательность действий, изложенную в части б) примера 1. При этом, исследователю нужно выбирать тип линии тренда, среди которых “Линейная”, “Логарифмическая”, “Полиномиальная”, “Степенная”, “Экспоненциальная”. На рис. 2 имеется одна из найденных линий криволинейной регресии.

|
|
|
|
|
|
99 |
|
|
Экспоненциальная корреляция |
|
|
||
|
80 |
|
y = 3,3796e0,757x |
|
|
|
|
|
|
|
|
|
|
|
70 |
|
|
|
|
|
|
60 |
|
|
|
|
|
|
50 |
|
|
|
|
|
y |
40 |
|
|
|
|
|
|
30 |
|
|
|
|
|
|
20 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
x |
|
|
Рис. 2. Корреляционное поле с экспоненциальной линией регрессии по данным примера 1 |
||||||
На полученных диаграммах будут представлены уравнения соответствующих линий регресии. Не приводя диаграммы, выпишем эти уравнения (табл. 3).
Как видно, выбор типов кривой регрессии достаточно большой. Какая же из этих кривых лучше сглаживает конкретную экспериментальную зависимость? Т.к. речь идёт о методе наименьших квадратов, то критерием выбора типа кривой будет сумма квадратов отклонений
n
∑[ yi − yx (xi )]2 .
i=1
Выбирать нужно кривую с наименьшим значением этой суммы.
Рассчитаем эти суммы по данным примера 1 для всех типов линии регрессии и поместим их также в табл. 3.
Табл. 3. Уравнения регресии и суммы квадратов отклонений, найденные с помощью Microsoft Excel по данным примера 1
Тип линии регрессии |
Уравнение |
Сумма квадратов откло- |
|
|
n |
|
|
нений ∑[ yi − yx (xi )]2 |
|
|
i=1 |
Линейная |
yx =18,934x −16,218 |
4023,08 |
Логарифмическая |
yx = 39,539ln(x) −0,9275 |
5046,28 |
Полиномиальная (сте- |
yx = 2,3632x2 +6,8478x −3,0234 |
3869,46 |
пень 2). Допускается вы- |
|
|
бор степени от 2 до 6. |
|
|
Степенная |
yx = 5,7263x1,6705 |
4115,27 |
Экспоненциальная |
yx = 3,3796e0,757 x |
5001,83 |
Следовательно, среди рассмотренных типов линий регрессии наилучшее приближение достигается при параболической корреляции второго порядка:
yx = 2,3632x2 +6,8478x −3,0234 .
3. До настоящего момента рассматривалась корреляционная связь между двумя количественными признаками. Если же исследуется связь между несколькими признаками, то корреляция называется множественной.

100
Рассмотрим простейший случай трёх признаков X ,Y , Z и предполагаемая связь меж-
ду ними линейная:
z = ax +by +c .
Нам необходимо решить три задачи: 1) найти выборочное уравнение связи, т.е. определить коэффициенты регрессии a и b и свободный член c ; 2) оценить тесноту связи между признаком Z и обоими признаками X ,Y ; 3) оценить тесноту связи между Z и X при постоян-
ном Y , между Z и Y при постоянном X .
Задача 1) решается методом наименьших квадратов. Заметим, что уравнение связи удобно искать в виде
z − z = a(x − x) +b( y − y) ,
где
a = |
rxz |
−ryz rxy |
|
s |
z |
, b = |
ryz |
−rxz rxy |
|
s |
z |
. |
1 |
−r 2 |
|
|
1−r 2 |
|
|
||||||
|
|
sx |
|
sy |
||||||||
|
|
xy |
|
|
|
|
|
xy |
|
|
|
|
Здесь rxz , ryz , rxy – выборочные коэффициенты корреляции между соответствующими признаками, sx , sy , sz – выборочные среднеквадратические отклонения.
Для решения задачи 2) вводят выборочный совокупный коэффициент корреляции, ко-
торый оценивает тесноту связи между признаком Z и обоими признаками X ,Y , и определяется формулой
r 2 |
−2r |
r |
r |
+ r |
2 |
R = xz |
xy |
xz |
yz |
yz |
, |
|
1− r |
2 |
|
|
|
|
|
xy |
|
|
|
причём 0 ≤ R ≤1.
3) Теснота связи между Z и X при постоянном Y , между Z и Y при постоянном X
оценивается соответствующими частными выборочными коэффициентами корреляции:
rxz( y) = |
rxz |
−rxy ryz |
, |
|
(1−r |
|
2 )(1−r |
||
|
|
2 ) |
||
|
xy |
yz |
|
|
ryz( x) = |
ryz |
−rxy rxz |
, |
|
(1−r |
|
2 )(1−r |
||
|
|
2 ) |
||
|
xy |
xz |
|
|
которые имеют те же свойства и тот же смысл, что и изучаемый ранее выборочный коэффициент корреляции. Они служат для оценки тесноты линейной связи между признаками.
|
ПримерU |
2.U Баскетболисты города представлены выборкой из 10 человек. У каждого из |
|||||||
|
|
x (кг), объём груди y (см) и рост z |
(см). Данные приведены в табл. 4. |
||||||
них измеряли вес |
|||||||||
|
|
|
|
|
|
Табл. 4. Данные о 10 баскетболистах города |
|||
|
|
|
|
№ |
Вес x (кг) |
Объём груди y (см) |
Рост z (см) |
|
|
|
|
|
|
1 |
120 |
113 |
|
194 |
|
|
|
|
|
2 |
80 |
102 |
|
183 |
|
|
|
|
|
3 |
100 |
115 |
|
200 |
|
|
|
|
|
4 |
90 |
108 |
|
190 |
|
|
|
|
|
5 |
95 |
116 |
|
195 |
|
|
|
|
|
6 |
88 |
105 |
|
190 |
|
|
|
|
|
7 |
89 |
110 |
|
191 |
|
|
|
|
|
8 |
91 |
109 |
|
187 |
|
|
|
|
|
9 |
87 |
110 |
|
192 |
|
|
|
|
|
10 |
70 |
95 |
|
180 |
|

101
Требуется: 1) найти выборочное уравнение связи, если предполагается, что эти признаки связаны линейно, т.е.
z= ax +by +c ;
2)определить выборочный совокупный коэффициент корреляции R ; 3) вычислить частные выборочные коэффициенты корреляции rxz( y) и ryz( x) .
Решение. 1) Уравнение связи имеет вид:
z − z = a(x − x) +b( y − y) .
Раскрывая скобки и приводя подобные, получим
z = ax +by + z −ax −by .
После определения коэффициентов регрессии a и b , найдём c = z − ax −by . Индивидуальные числовые характеристики выборки таковы:
x = 91; y =108,3; z =190,2; sx =12,3693; sy = 6,00083; sz = 5,50999 .
Рассчитаем теперь совместные выборочные характеристики:
rxy = 0,77601; rxz = 0,73803; ryz = 0,92062 .
Подставляя вычисленные характеристики в соответствующие формулы, получим значения параметров:
a = 0,02644; b = 0,80302; c =100,826 .
Следовательно, искомое уравнение связи имеет вид:
z= 0,02644x +0,80302 y +100,826 .
2)Выборочный совокупный коэффициент корреляции
R = 0,92138 ,
что свидетельствует о высокой степени тесноты линейной связи. 3) Частные выборочные коэффициенты корреляции:
rxz ( y) = 0,09589 ; ryz( x) = 0,81747 .
Пример выполнен полностью.
ЗамечаниеU 2.U Множественная корреляция часто возникает в эконометрических задачах. Например, важным показателем акции является скорректированный «бета»- коэффициент βa . Он зависит от следующих количественных признаков: as – параметр, ха-
рактеризующий сектор экономики; βh – статистический «бета»-коэффициент; Y – диви-
дендная доходность компании; S – параметр, характеризующий «размер» компании (десятичный логарифм от суммарной рыночной стоимости акций, выраженной в млрд. долл.). Уравнение связи ищется в таком виде:
βa = as +с1βh +с2Y +с3 S .
Т.е. определению подлежат коэффициенты регрессии с1 ,с2 ,с3 . Исследования рынка США
показали, например, что в конце 70-х гг. «бета»-коэффициенты хорошо корректировались следующим соотношением:
βa = as +0,576βh −0,019Y −0,105S .
102
ЗАКЛЮЧЕНИЕU
Завершая курс лекций, следует отметить, что ТВиМС – развивающаяся наука, из недр которой возникли теория случайных процессов, теория массового обслуживания, теория информации и др. прикладные и теоретические научные направления.
Для студентов-экономистов наибольшее значение, пожалуй, имеет тот факт, что основываясь на вероятностных методах, сформировалась отдельная наука – эконометрия. Этот предмет обычно изучают на третьем курсе. А среди разделов математического программирования отдельно выделяют стохастическое программирование.
Автор надеется на сотрудничество и ожидает дельных рекомендаций по улучшению качества лекций.
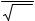
103
ПРИЛОЖЕНИЯU
|
|
|
|
|
|
|
|
|
1 |
|
|
|
Приложение 1 |
|
|
|
Таблица значений функции Лапласа ϕ(x) = |
|
e−x2 / 2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
ϕ(x) |
x |
ϕ(x) |
x |
ϕ(x) |
x |
ϕ(x) |
|
x |
|
ϕ(x) |
x |
ϕ(x) |
|
0 |
0,3989 |
0,7 |
0,3123 |
1,4 |
0,1497 |
2,1 |
0,0440 |
|
2,8 |
|
0,0079 |
3,5 |
0,0009 |
|
0,01 |
0,3989 |
0,71 |
0,3101 |
1,41 |
0,1476 |
2,11 |
0,0431 |
|
2,81 |
|
0,0077 |
3,51 |
0,0008 |
|
0,02 |
0,3989 |
0,72 |
0,3079 |
1,42 |
0,1456 |
2,12 |
0,0422 |
|
2,82 |
|
0,0075 |
3,52 |
0,0008 |
|
0,03 |
0,3988 |
0,73 |
0,3056 |
1,43 |
0,1435 |
2,13 |
0,0413 |
|
2,83 |
|
0,0073 |
3,53 |
0,0008 |
|
0,04 |
0,3986 |
0,74 |
0,3034 |
1,44 |
0,1415 |
2,14 |
0,0404 |
|
2,84 |
|
0,0071 |
3,54 |
0,0008 |
|
0,05 |
0,3984 |
0,75 |
0,3011 |
1,45 |
0,1394 |
2,15 |
0,0396 |
|
2,85 |
|
0,0069 |
3,55 |
0,0007 |
|
0,06 |
0,3982 |
0,76 |
0,2989 |
1,46 |
0,1374 |
2,16 |
0,0387 |
|
2,86 |
|
0,0067 |
3,56 |
0,0007 |
|
0,07 |
0,3980 |
0,77 |
0,2966 |
1,47 |
0,1354 |
2,17 |
0,0379 |
|
2,87 |
|
0,0065 |
3,57 |
0,0007 |
|
0,08 |
0,3977 |
0,78 |
0,2943 |
1,48 |
0,1334 |
2,18 |
0,0371 |
|
2,88 |
|
0,0063 |
3,58 |
0,0007 |
|
0,09 |
0,3973 |
0,79 |
0,2920 |
1,49 |
0,1315 |
2,19 |
0,0363 |
|
2,89 |
|
0,0061 |
3,59 |
0,0006 |
|
0,1 |
0,3970 |
0,8 |
0,2897 |
1,5 |
0,1295 |
2,2 |
0,0355 |
|
2,9 |
|
0,0060 |
3,6 |
0,0006 |
|
0,11 |
0,3965 |
0,81 |
0,2874 |
1,51 |
0,1276 |
2,21 |
0,0347 |
|
2,91 |
|
0,0058 |
3,61 |
0,0006 |
|
0,12 |
0,3961 |
0,82 |
0,2850 |
1,52 |
0,1257 |
2,22 |
0,0339 |
|
2,92 |
|
0,0056 |
3,62 |
0,0006 |
|
0,13 |
0,3956 |
0,83 |
0,2827 |
1,53 |
0,1238 |
2,23 |
0,0332 |
|
2,93 |
|
0,0055 |
3,63 |
0,0005 |
|
0,14 |
0,3951 |
0,84 |
0,2803 |
1,54 |
0,1219 |
2,24 |
0,0325 |
|
2,94 |
|
0,0053 |
3,64 |
0,0005 |
|
0,15 |
0,3945 |
0,85 |
0,2780 |
1,55 |
0,1200 |
2,25 |
0,0317 |
|
2,95 |
|
0,0051 |
3,65 |
0,0005 |
|
0,16 |
0,3939 |
0,86 |
0,2756 |
1,56 |
0,1182 |
2,26 |
0,0310 |
|
2,96 |
|
0,0050 |
3,66 |
0,0005 |
|
0,17 |
0,3932 |
0,87 |
0,2732 |
1,57 |
0,1163 |
2,27 |
0,0303 |
|
2,97 |
|
0,0048 |
3,67 |
0,0005 |
|
0,18 |
0,3925 |
0,88 |
0,2709 |
1,58 |
0,1145 |
2,28 |
0,0297 |
|
2,98 |
|
0,0047 |
3,68 |
0,0005 |
|
0,19 |
0,3918 |
0,89 |
0,2685 |
1,59 |
0,1127 |
2,29 |
0,0290 |
|
2,99 |
|
0,0046 |
3,69 |
0,0004 |
|
0,2 |
0,3910 |
0,9 |
0,2661 |
1,6 |
0,1109 |
2,3 |
0,0283 |
|
3 |
|
0,0044 |
3,7 |
0,0004 |
|
0,21 |
0,3902 |
0,91 |
0,2637 |
1,61 |
0,1092 |
2,31 |
0,0277 |
|
3,01 |
|
0,0043 |
3,71 |
0,0004 |
|
0,22 |
0,3894 |
0,92 |
0,2613 |
1,62 |
0,1074 |
2,32 |
0,0270 |
|
3,02 |
|
0,0042 |
3,72 |
0,0004 |
|
0,23 |
0,3885 |
0,93 |
0,2589 |
1,63 |
0,1057 |
2,33 |
0,0264 |
|
3,03 |
|
0,0040 |
3,73 |
0,0004 |
|
0,24 |
0,3876 |
0,94 |
0,2565 |
1,64 |
0,1040 |
2,34 |
0,0258 |
|
3,04 |
|
0,0039 |
3,74 |
0,0004 |
|
0,25 |
0,3867 |
0,95 |
0,2541 |
1,65 |
0,1023 |
2,35 |
0,0252 |
|
3,05 |
|
0,0038 |
3,75 |
0,0004 |
|
0,26 |
0,3857 |
0,96 |
0,2516 |
1,66 |
0,1006 |
2,36 |
0,0246 |
|
3,06 |
|
0,0037 |
3,76 |
0,0003 |
|
0,27 |
0,3847 |
0,97 |
0,2492 |
1,67 |
0,0989 |
2,37 |
0,0241 |
|
3,07 |
|
0,0036 |
3,77 |
0,0003 |
|
0,28 |
0,3836 |
0,98 |
0,2468 |
1,68 |
0,0973 |
2,38 |
0,0235 |
|
3,08 |
|
0,0035 |
3,78 |
0,0003 |
|
0,29 |
0,3825 |
0,99 |
0,2444 |
1,69 |
0,0957 |
2,39 |
0,0229 |
|
3,09 |
|
0,0034 |
3,79 |
0,0003 |
|
0,3 |
0,3814 |
1 |
0,2420 |
1,7 |
0,0940 |
2,4 |
0,0224 |
|
3,1 |
|
0,0033 |
3,8 |
0,0003 |
|
0,31 |
0,3802 |
1,01 |
0,2396 |
1,71 |
0,0925 |
2,41 |
0,0219 |
|
3,11 |
|
0,0032 |
3,81 |
0,0003 |
|
0,32 |
0,3790 |
1,02 |
0,2371 |
1,72 |
0,0909 |
2,42 |
0,0213 |
|
3,12 |
|
0,0031 |
3,82 |
0,0003 |
|
0,33 |
0,3778 |
1,03 |
0,2347 |
1,73 |
0,0893 |
2,43 |
0,0208 |
|
3,13 |
|
0,0030 |
3,83 |
0,0003 |
|
0,34 |
0,3765 |
1,04 |
0,2323 |
1,74 |
0,0878 |
2,44 |
0,0203 |
|
3,14 |
|
0,0029 |
3,84 |
0,0003 |
|
0,35 |
0,3752 |
1,05 |
0,2299 |
1,75 |
0,0863 |
2,45 |
0,0198 |
|
3,15 |
|
0,0028 |
3,85 |
0,0002 |
|
0,36 |
0,3739 |
1,06 |
0,2275 |
1,76 |
0,0848 |
2,46 |
0,0194 |
|
3,16 |
|
0,0027 |
3,86 |
0,0002 |
|
0,37 |
0,3725 |
1,07 |
0,2251 |
1,77 |
0,0833 |
2,47 |
0,0189 |
|
3,17 |
|
0,0026 |
3,87 |
0,0002 |
|
0,38 |
0,3712 |
1,08 |
0,2227 |
1,78 |
0,0818 |
2,48 |
0,0184 |
|
3,18 |
|
0,0025 |
3,88 |
0,0002 |
|
0,39 |
0,3697 |
1,09 |
0,2203 |
1,79 |
0,0804 |
2,49 |
0,0180 |
|
3,19 |
|
0,0025 |
3,89 |
0,0002 |
|
0,4 |
0,3683 |
1,1 |
0,2179 |
1,8 |
0,0790 |
2,5 |
0,0175 |
|
3,2 |
|
0,0024 |
3,9 |
0,0002 |
|
0,41 |
0,3668 |
1,11 |
0,2155 |
1,81 |
0,0775 |
2,51 |
0,0171 |
|
3,21 |
|
0,0023 |
3,91 |
0,0002 |
|
0,42 |
0,3653 |
1,12 |
0,2131 |
1,82 |
0,0761 |
2,52 |
0,0167 |
|
3,22 |
|
0,0022 |
3,92 |
0,0002 |
|
0,43 |
0,3637 |
1,13 |
0,2107 |
1,83 |
0,0748 |
2,53 |
0,0163 |
|
3,23 |
|
0,0022 |
3,93 |
0,0002 |
|
0,44 |
0,3621 |
1,14 |
0,2083 |
1,84 |
0,0734 |
2,54 |
0,0158 |
|
3,24 |
|
0,0021 |
3,94 |
0,0002 |
|
0,45 |
0,3605 |
1,15 |
0,2059 |
1,85 |
0,0721 |
2,55 |
0,0154 |
|
3,25 |
|
0,0020 |
3,95 |
0,0002 |
|
0,46 |
0,3589 |
1,16 |
0,2036 |
1,86 |
0,0707 |
2,56 |
0,0151 |
|
3,26 |
|
0,0020 |
3,96 |
0,0002 |
|
0,47 |
0,3572 |
1,17 |
0,2012 |
1,87 |
0,0694 |
2,57 |
0,0147 |
|
3,27 |
|
0,0019 |
3,97 |
0,0002 |
|
104
Окончание приложения 1
|
|
|
|
|
|
|
|
|
|
|
|
x |
ϕ(x) |
x |
ϕ(x) |
x |
ϕ(x) |
x |
ϕ(x) |
x |
ϕ(x) |
x |
ϕ(x) |
0,48 |
0,3555 |
1,18 |
0,1989 |
1,88 |
0,0681 |
2,58 |
0,0143 |
3,28 |
0,0018 |
3,98 |
0,0001 |
0,49 |
0,3538 |
1,19 |
0,1965 |
1,89 |
0,0669 |
2,59 |
0,0139 |
3,29 |
0,0018 |
3,99 |
0,0001 |
0,5 |
0,3521 |
1,2 |
0,1942 |
1,9 |
0,0656 |
2,6 |
0,0136 |
3,3 |
0,0017 |
4 |
0,0001 |
0,51 |
0,3503 |
1,21 |
0,1919 |
1,91 |
0,0644 |
2,61 |
0,0132 |
3,31 |
0,0017 |
4,01 |
0,0001 |
0,52 |
0,3485 |
1,22 |
0,1895 |
1,92 |
0,0632 |
2,62 |
0,0129 |
3,32 |
0,0016 |
4,02 |
0,0001 |
0,53 |
0,3467 |
1,23 |
0,1872 |
1,93 |
0,0620 |
2,63 |
0,0126 |
3,33 |
0,0016 |
4,03 |
0,0001 |
0,54 |
0,3448 |
1,24 |
0,1849 |
1,94 |
0,0608 |
2,64 |
0,0122 |
3,34 |
0,0015 |
4,04 |
0,0001 |
0,55 |
0,3429 |
1,25 |
0,1826 |
1,95 |
0,0596 |
2,65 |
0,0119 |
3,35 |
0,0015 |
4,05 |
0,0001 |
0,56 |
0,3410 |
1,26 |
0,1804 |
1,96 |
0,0584 |
2,66 |
0,0116 |
3,36 |
0,0014 |
4,06 |
0,0001 |
0,57 |
0,3391 |
1,27 |
0,1781 |
1,97 |
0,0573 |
2,67 |
0,0113 |
3,37 |
0,0014 |
4,07 |
0,0001 |
0,58 |
0,3372 |
1,28 |
0,1758 |
1,98 |
0,0562 |
2,68 |
0,0110 |
3,38 |
0,0013 |
4,08 |
0,0001 |
0,59 |
0,3352 |
1,29 |
0,1736 |
1,99 |
0,0551 |
2,69 |
0,0107 |
3,39 |
0,0013 |
4,09 |
0,0001 |
0,6 |
0,3332 |
1,3 |
0,1714 |
2 |
0,0540 |
2,7 |
0,0104 |
3,4 |
0,0012 |
4,1 |
0,0001 |
0,61 |
0,3312 |
1,31 |
0,1691 |
2,01 |
0,0529 |
2,71 |
0,0101 |
3,41 |
0,0012 |
4,11 |
0,0001 |
0,62 |
0,3292 |
1,32 |
0,1669 |
2,02 |
0,0519 |
2,72 |
0,0099 |
3,42 |
0,0012 |
4,12 |
0,0001 |
0,63 |
0,3271 |
1,33 |
0,1647 |
2,03 |
0,0508 |
2,73 |
0,0096 |
3,43 |
0,0011 |
4,13 |
0,0001 |
0,64 |
0,3251 |
1,34 |
0,1626 |
2,04 |
0,0498 |
2,74 |
0,0093 |
3,44 |
0,0011 |
4,14 |
0,0001 |
0,65 |
0,3230 |
1,35 |
0,1604 |
2,05 |
0,0488 |
2,75 |
0,0091 |
3,45 |
0,0010 |
4,15 |
0,0001 |
0,66 |
0,3209 |
1,36 |
0,1582 |
2,06 |
0,0478 |
2,76 |
0,0088 |
3,46 |
0,0010 |
4,16 |
0,0001 |
0,67 |
0,3187 |
1,37 |
0,1561 |
2,07 |
0,0468 |
2,77 |
0,0086 |
3,47 |
0,0010 |
4,17 |
0,0001 |
0,68 |
0,3166 |
1,38 |
0,1539 |
2,08 |
0,0459 |
2,78 |
0,0084 |
3,48 |
0,0009 |
4,18 |
0,0001 |
0,69 |
0,3144 |
1,39 |
0,1518 |
2,09 |
0,0449 |
2,79 |
0,0081 |
3,49 |
0,0009 |
4,19 |
0,0001 |
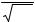
105
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 2 |
|
|
Таблица значений интегральной функции Лапласа Φ(x) = |
1 |
∫x e−z2 / 2 dz |
|||||||||||
|
|
|
|
|
|
|
|
|
|
2π |
0 |
|
|
|
x |
Φ(x) |
x |
Φ(x) |
x |
Φ(x) |
x |
Φ(x) |
x |
Φ(x) |
|
x |
Φ(x) |
|
|
0 |
0 |
0,9 |
0,3159 |
1,8 |
0,4641 |
2,7 |
0,4965 |
3,6 |
0,499841 |
4,5 |
0,4999966 |
|
||
0,01 |
0,004 |
0,91 |
0,3186 |
1,81 |
0,4649 |
2,71 |
0,4966 |
3,61 |
0,499847 |
4,51 |
0,4999968 |
|
||
0,02 |
0,008 |
0,92 |
0,3212 |
1,82 |
0,4656 |
2,72 |
0,4967 |
3,62 |
0,499853 |
4,52 |
0,4999969 |
|
||
0,03 |
0,012 |
0,93 |
0,3238 |
1,83 |
0,4664 |
2,73 |
0,4968 |
3,63 |
0,499858 |
4,53 |
0,499997 |
|
||
0,04 |
0,016 |
0,94 |
0,3264 |
1,84 |
0,4671 |
2,74 |
0,4969 |
3,64 |
0,499864 |
4,54 |
0,4999972 |
|
||
0,05 |
0,0199 |
0,95 |
0,3289 |
1,85 |
0,4678 |
2,75 |
0,497 |
3,65 |
0,499869 |
4,55 |
0,4999973 |
|
||
0,06 |
0,0239 |
0,96 |
0,3315 |
1,86 |
0,4686 |
2,76 |
0,4971 |
3,66 |
0,499874 |
4,56 |
0,4999974 |
|
||
0,07 |
0,0279 |
0,97 |
0,334 |
1,87 |
0,4693 |
2,77 |
0,4972 |
3,67 |
0,499879 |
4,57 |
0,4999976 |
|
||
0,08 |
0,0319 |
0,98 |
0,3365 |
1,88 |
0,4699 |
2,78 |
0,4973 |
3,68 |
0,499883 |
4,58 |
0,4999977 |
|
||
0,09 |
0,0359 |
0,99 |
0,3389 |
1,89 |
0,4706 |
2,79 |
0,4974 |
3,69 |
0,499888 |
4,59 |
0,4999978 |
|
||
0,1 |
0,0398 |
1 |
0,3413 |
1,9 |
0,4713 |
2,8 |
0,4974 |
3,7 |
0,499892 |
4,6 |
0,4999979 |
|
||
0,11 |
0,0438 |
1,01 |
0,3438 |
1,91 |
0,4719 |
2,81 |
0,4975 |
3,71 |
0,499896 |
4,61 |
0,499998 |
|
||
0,12 |
0,0478 |
1,02 |
0,3461 |
1,92 |
0,4726 |
2,82 |
0,4976 |
3,72 |
0,4999 |
4,62 |
0,4999981 |
|
||
0,13 |
0,0517 |
1,03 |
0,3485 |
1,93 |
0,4732 |
2,83 |
0,4977 |
3,73 |
0,499904 |
4,63 |
0,4999982 |
|
||
0,14 |
0,0557 |
1,04 |
0,3508 |
1,94 |
0,4738 |
2,84 |
0,4977 |
3,74 |
0,499908 |
4,64 |
0,4999983 |
|
||
0,15 |
0,0596 |
1,05 |
0,3531 |
1,95 |
0,4744 |
2,85 |
0,4978 |
3,75 |
0,499912 |
4,65 |
0,4999983 |
|
||
0,16 |
0,0636 |
1,06 |
0,3554 |
1,96 |
0,475 |
2,86 |
0,4979 |
3,76 |
0,499915 |
4,66 |
0,4999984 |
|
||
0,17 |
0,0675 |
1,07 |
0,3577 |
1,97 |
0,4756 |
2,87 |
0,4979 |
3,77 |
0,499918 |
4,67 |
0,4999985 |
|
||
0,18 |
0,0714 |
1,08 |
0,3599 |
1,98 |
0,4761 |
2,88 |
0,498 |
3,78 |
0,499922 |
4,68 |
0,4999986 |
|
||
0,19 |
0,0753 |
1,09 |
0,3621 |
1,99 |
0,4767 |
2,89 |
0,4981 |
3,79 |
0,499925 |
4,69 |
0,4999986 |
|
||
0,2 |
0,0793 |
1,1 |
0,3643 |
2 |
0,4772 |
2,9 |
0,4981 |
3,8 |
0,499928 |
4,7 |
0,4999987 |
|
||
0,21 |
0,0832 |
1,11 |
0,3665 |
2,01 |
0,4778 |
2,91 |
0,4982 |
3,81 |
0,49993 |
4,71 |
0,4999988 |
|
||
0,22 |
0,0871 |
1,12 |
0,3686 |
2,02 |
0,4783 |
2,92 |
0,4982 |
3,82 |
0,499933 |
4,72 |
0,4999988 |
|
||
0,23 |
0,091 |
1,13 |
0,3708 |
2,03 |
0,4788 |
2,93 |
0,4983 |
3,83 |
0,499936 |
4,73 |
0,4999989 |
|
||
0,24 |
0,0948 |
1,14 |
0,3729 |
2,04 |
0,4793 |
2,94 |
0,4984 |
3,84 |
0,499938 |
4,74 |
0,4999989 |
|
||
0,25 |
0,0987 |
1,15 |
0,3749 |
2,05 |
0,4798 |
2,95 |
0,4984 |
3,85 |
0,499941 |
4,75 |
0,499999 |
|
||
0,26 |
0,1026 |
1,16 |
0,377 |
2,06 |
0,4803 |
2,96 |
0,4985 |
3,86 |
0,499943 |
4,76 |
0,499999 |
|
||
0,27 |
0,1064 |
1,17 |
0,379 |
2,07 |
0,4808 |
2,97 |
0,4985 |
3,87 |
0,499946 |
4,77 |
0,4999991 |
|
||
0,28 |
0,1103 |
1,18 |
0,381 |
2,08 |
0,4812 |
2,98 |
0,4986 |
3,88 |
0,499948 |
4,78 |
0,4999991 |
|
||
0,29 |
0,1141 |
1,19 |
0,383 |
2,09 |
0,4817 |
2,99 |
0,4986 |
3,89 |
0,49995 |
4,79 |
0,4999992 |
|
||
0,3 |
0,1179 |
1,2 |
0,3849 |
2,1 |
0,4821 |
3 |
0,4987 |
3,9 |
0,499952 |
4,8 |
0,4999992 |
|
||
0,31 |
0,1217 |
1,21 |
0,3869 |
2,11 |
0,4826 |
3,01 |
0,4987 |
3,91 |
0,499954 |
4,81 |
0,4999992 |
|
||
0,32 |
0,1255 |
1,22 |
0,3888 |
2,12 |
0,483 |
3,02 |
0,4987 |
3,92 |
0,499956 |
4,82 |
0,4999993 |
|
||
0,33 |
0,1293 |
1,23 |
0,3907 |
2,13 |
0,4834 |
3,03 |
0,4988 |
3,93 |
0,499958 |
4,83 |
0,4999993 |
|
||
0,34 |
0,1331 |
1,24 |
0,3925 |
2,14 |
0,4838 |
3,04 |
0,4988 |
3,94 |
0,499959 |
4,84 |
0,4999993 |
|
||
0,35 |
0,1368 |
1,25 |
0,3944 |
2,15 |
0,4842 |
3,05 |
0,4989 |
3,95 |
0,499961 |
4,85 |
0,4999994 |
|
||
0,36 |
0,1406 |
1,26 |
0,3962 |
2,16 |
0,4846 |
3,06 |
0,4989 |
3,96 |
0,499963 |
4,86 |
0,4999994 |
|
||
0,37 |
0,1443 |
1,27 |
0,398 |
2,17 |
0,485 |
3,07 |
0,4989 |
3,97 |
0,499964 |
4,87 |
0,4999994 |
|
||
0,38 |
0,148 |
1,28 |
0,3997 |
2,18 |
0,4854 |
3,08 |
0,499 |
3,98 |
0,499966 |
4,88 |
0,4999995 |
|
||
0,39 |
0,1517 |
1,29 |
0,4015 |
2,19 |
0,4857 |
3,09 |
0,499 |
3,99 |
0,499967 |
4,89 |
0,4999995 |
|
||
0,4 |
0,1554 |
1,3 |
0,4032 |
2,2 |
0,4861 |
3,1 |
0,499 |
4 |
0,499968 |
4,9 |
0,4999995 |
|
||
0,41 |
0,1591 |
1,31 |
0,4049 |
2,21 |
0,4864 |
3,11 |
0,4991 |
4,01 |
0,49997 |
4,91 |
0,4999995 |
|
||
0,42 |
0,1628 |
1,32 |
0,4066 |
2,22 |
0,4868 |
3,12 |
0,4991 |
4,02 |
0,499971 |
4,92 |
0,4999996 |
|
||
0,43 |
0,1664 |
1,33 |
0,4082 |
2,23 |
0,4871 |
3,13 |
0,4991 |
4,03 |
0,499972 |
4,93 |
0,4999996 |
|
||
0,44 |
0,17 |
1,34 |
0,4099 |
2,24 |
0,4875 |
3,14 |
0,4992 |
4,04 |
0,499973 |
4,94 |
0,4999996 |
|
||
0,45 |
0,1736 |
1,35 |
0,4115 |
2,25 |
0,4878 |
3,15 |
0,4992 |
4,05 |
0,499974 |
4,95 |
0,4999996 |
|
||
0,46 |
0,1772 |
1,36 |
0,4131 |
2,26 |
0,4881 |
3,16 |
0,4992 |
4,06 |
0,499975 |
4,96 |
0,4999996 |
|
||
0,47 |
0,1808 |
1,37 |
0,4147 |
2,27 |
0,4884 |
3,17 |
0,4992 |
4,07 |
0,499976 |
4,97 |
0,4999997 |
|
||
0,48 |
0,1844 |
1,38 |
0,4162 |
2,28 |
0,4887 |
3,18 |
0,4993 |
4,08 |
0,499977 |
4,98 |
0,4999997 |
|
||
0,49 |
0,1879 |
1,39 |
0,4177 |
2,29 |
0,489 |
3,19 |
0,4993 |
4,09 |
0,499978 |
4,99 |
0,4999997 |
|
||
0,5 |
0,1915 |
1,4 |
0,4192 |
2,3 |
0,4893 |
3,2 |
0,4993 |
4,1 |
0,499979 |
5 |
0,4999997 |
|
||
|
|
|
|
|
|
|
|
|
|
|
106 |
|
|
|
|
|
|
|
|
|
|
|
Окончание приложения 2 |
||
x |
Φ(x) |
x |
Φ(x) |
x |
Φ(x) |
x |
Φ(x) |
x |
Φ(x) |
x |
Φ(x) |
|
0,51 |
0,195 |
1,41 |
0,4207 |
2,31 |
0,4896 |
3,21 |
0,4993 |
4,11 |
0,49998 |
5,01 |
0,4999997 |
|
0,52 |
0,1985 |
1,42 |
0,4222 |
2,32 |
0,4898 |
3,22 |
0,4994 |
4,12 |
0,499981 |
5,02 |
0,4999997 |
|
0,53 |
0,2019 |
1,43 |
0,4236 |
2,33 |
0,4901 |
3,23 |
0,4994 |
4,13 |
0,499982 |
5,03 |
0,4999998 |
|
0,54 |
0,2054 |
1,44 |
0,4251 |
2,34 |
0,4904 |
3,24 |
0,4994 |
4,14 |
0,499983 |
5,04 |
0,4999998 |
|
0,55 |
0,2088 |
1,45 |
0,4265 |
2,35 |
0,4906 |
3,25 |
0,4994 |
4,15 |
0,499983 |
5,05 |
0,4999998 |
|
0,56 |
0,2123 |
1,46 |
0,4279 |
2,36 |
0,4909 |
3,26 |
0,4994 |
4,16 |
0,499984 |
5,06 |
0,4999998 |
|
0,57 |
0,2157 |
1,47 |
0,4292 |
2,37 |
0,4911 |
3,27 |
0,4995 |
4,17 |
0,499985 |
5,07 |
0,4999998 |
|
0,58 |
0,219 |
1,48 |
0,4306 |
2,38 |
0,4913 |
3,28 |
0,4995 |
4,18 |
0,499985 |
5,08 |
0,4999998 |
|
0,59 |
0,2224 |
1,49 |
0,4319 |
2,39 |
0,4916 |
3,29 |
0,4995 |
4,19 |
0,499986 |
5,09 |
0,4999998 |
|
0,6 |
0,2257 |
1,5 |
0,4332 |
2,4 |
0,4918 |
3,3 |
0,4995 |
4,2 |
0,499987 |
5,1 |
0,4999998 |
|
0,61 |
0,2291 |
1,51 |
0,4345 |
2,41 |
0,492 |
3,31 |
0,4995 |
4,21 |
0,499987 |
5,11 |
0,4999998 |
|
0,62 |
0,2324 |
1,52 |
0,4357 |
2,42 |
0,4922 |
3,32 |
0,4995 |
4,22 |
0,499988 |
5,12 |
0,4999998 |
|
0,63 |
0,2357 |
1,53 |
0,437 |
2,43 |
0,4925 |
3,33 |
0,4996 |
4,23 |
0,499988 |
5,13 |
0,4999999 |
|
0,64 |
0,2389 |
1,54 |
0,4382 |
2,44 |
0,4927 |
3,34 |
0,4996 |
4,24 |
0,499989 |
5,14 |
0,4999999 |
|
0,65 |
0,2422 |
1,55 |
0,4394 |
2,45 |
0,4929 |
3,35 |
0,4996 |
4,25 |
0,499989 |
5,15 |
0,4999999 |
|
0,66 |
0,2454 |
1,56 |
0,4406 |
2,46 |
0,4931 |
3,36 |
0,4996 |
4,26 |
0,49999 |
5,16 |
0,4999999 |
|
0,67 |
0,2486 |
1,57 |
0,4418 |
2,47 |
0,4932 |
3,37 |
0,4996 |
4,27 |
0,49999 |
5,17 |
0,4999999 |
|
0,68 |
0,2517 |
1,58 |
0,4429 |
2,48 |
0,4934 |
3,38 |
0,4996 |
4,28 |
0,499991 |
5,18 |
0,4999999 |
|
0,69 |
0,2549 |
1,59 |
0,4441 |
2,49 |
0,4936 |
3,39 |
0,4997 |
4,29 |
0,499991 |
5,19 |
0,4999999 |
|
0,7 |
0,258 |
1,6 |
0,4452 |
2,5 |
0,4938 |
3,4 |
0,4997 |
4,3 |
0,499991 |
5,2 |
0,4999999 |
|
0,71 |
0,2611 |
1,61 |
0,4463 |
2,51 |
0,494 |
3,41 |
0,4997 |
4,31 |
0,499992 |
5,21 |
0,4999999 |
|
0,72 |
0,2642 |
1,62 |
0,4474 |
2,52 |
0,4941 |
3,42 |
0,4997 |
4,32 |
0,499992 |
5,22 |
0,4999999 |
|
0,73 |
0,2673 |
1,63 |
0,4484 |
2,53 |
0,4943 |
3,43 |
0,4997 |
4,33 |
0,499993 |
5,23 |
0,4999999 |
|
0,74 |
0,2704 |
1,64 |
0,4495 |
2,54 |
0,4945 |
3,44 |
0,4997 |
4,34 |
0,499993 |
5,24 |
0,4999999 |
|
0,75 |
0,2734 |
1,65 |
0,4505 |
2,55 |
0,4946 |
3,45 |
0,4997 |
4,35 |
0,499993 |
5,25 |
0,4999999 |
|
0,76 |
0,2764 |
1,66 |
0,4515 |
2,56 |
0,4948 |
3,46 |
0,4997 |
4,36 |
0,499993 |
5,26 |
0,4999999 |
|
0,77 |
0,2794 |
1,67 |
0,4525 |
2,57 |
0,4949 |
3,47 |
0,4997 |
4,37 |
0,499994 |
5,27 |
0,4999999 |
|
0,78 |
0,2823 |
1,68 |
0,4535 |
2,58 |
0,4951 |
3,48 |
0,4997 |
4,38 |
0,499994 |
5,28 |
0,4999999 |
|
0,79 |
0,2852 |
1,69 |
0,4545 |
2,59 |
0,4952 |
3,49 |
0,4998 |
4,39 |
0,499994 |
5,29 |
0,4999999 |
|
0,8 |
0,2881 |
1,7 |
0,4554 |
2,6 |
0,4953 |
3,5 |
0,4998 |
4,4 |
0,499995 |
5,3 |
0,4999999 |
|
0,81 |
0,291 |
1,71 |
0,4564 |
2,61 |
0,4955 |
3,51 |
0,4998 |
4,41 |
0,499995 |
5,31 |
0,4999999 |
|
0,82 |
0,2939 |
1,72 |
0,4573 |
2,62 |
0,4956 |
3,52 |
0,4998 |
4,42 |
0,499995 |
5,32 |
0,4999999 |
|
0,83 |
0,2967 |
1,73 |
0,4582 |
2,63 |
0,4957 |
3,53 |
0,4998 |
4,43 |
0,499995 |
5,33 |
0,5 |
|
0,84 |
0,2995 |
1,74 |
0,4591 |
2,64 |
0,4959 |
3,54 |
0,4998 |
4,44 |
0,499995 |
5,34 |
0,5 |
|
0,85 |
0,3023 |
1,75 |
0,4599 |
2,65 |
0,496 |
3,55 |
0,4998 |
4,45 |
0,499996 |
5,35 |
0,5 |
|
0,86 |
0,3051 |
1,76 |
0,4608 |
2,66 |
0,4961 |
3,56 |
0,4998 |
4,46 |
0,499996 |
5,36 |
0,5 |
|
0,87 |
0,3078 |
1,77 |
0,4616 |
2,67 |
0,4962 |
3,57 |
0,4998 |
4,47 |
0,499996 |
5,37 |
0,5 |
|
0,88 |
0,3106 |
1,78 |
0,4625 |
2,68 |
0,4963 |
3,58 |
0,4998 |
4,48 |
0,499996 |
5,38 |
0,5 |
|
0,89 |
0,3133 |
1,79 |
0,4633 |
2,69 |
0,4964 |
3,59 |
0,4998 |
4,49 |
0,499996 |
5,39 |
0,5 |
|
107
|
|
Таблица значений tγ |
= t(γ , n) |
|
Приложение 3 |
|||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
n |
|
γ |
|
n |
|
γ |
|
|
0,95 |
0,99 |
0,999 |
0,95 |
0,99 |
0,999 |
|
||
5 |
2,776451 |
4,60408 |
8,610077 |
20 |
2,093025 |
2,860943 |
3,883324 |
|
6 |
2,570578 |
4,032117 |
6,868504 |
25 |
2,063898 |
2,796951 |
3,745372 |
|
7 |
2,446914 |
3,707428 |
5,958718 |
30 |
2,045231 |
2,756387 |
3,659516 |
|
8 |
2,364623 |
3,499481 |
5,408074 |
35 |
2,032243 |
2,728393 |
3,600726 |
|
9 |
2,306006 |
3,355381 |
5,041366 |
40 |
2,022689 |
2,707911 |
3,558089 |
|
10 |
2,262159 |
3,249843 |
4,780886 |
45 |
2,015367 |
2,692286 |
3,525784 |
|
11 |
2,228139 |
3,169262 |
4,586764 |
50 |
2,009574 |
2,679953 |
3,500463 |
|
12 |
2,200986 |
3,105815 |
4,436879 |
60 |
2,000997 |
2,661764 |
3,46321 |
|
13 |
2,178813 |
3,054538 |
4,317844 |
70 |
1,994945 |
2,648976 |
3,437162 |
|
14 |
2,160368 |
3,012283 |
4,220929 |
80 |
1,990452 |
2,639499 |
3,417954 |
|
15 |
2,144789 |
2,976849 |
4,140311 |
90 |
1,986978 |
2,632205 |
3,403256 |
|
16 |
2,131451 |
2,946726 |
4,07279 |
100 |
1,984217 |
2,626402 |
3,391469 |
|
17 |
2,119905 |
2,920788 |
4,014873 |
120 |
1,980097 |
2,61778 |
3,374153 |
|
18 |
2,109819 |
2,898232 |
3,965106 |
∞ |
1,96 |
2,576 |
3,291 |
|
19 |
2,100924 |
2,878442 |
3,921741 |
|
|
|
|
|
Приложение 4
Таблица значений q = q(γ , n)
n |
|
γ |
|
n |
|
γ |
|
0,95 |
0,99 |
0,999 |
0,95 |
0,99 |
0,999 |
||
5 |
1,372354 |
2,669219 |
5,637076 |
20 |
0,370411 |
0,577748 |
0,874616 |
6 |
1,089256 |
2,003404 |
3,876984 |
25 |
0,316453 |
0,486838 |
0,722958 |
7 |
0,91543 |
1,62299 |
2,968182 |
30 |
0,279704 |
0,426244 |
0,624712 |
8 |
0,797151 |
1,376883 |
2,419917 |
35 |
0,252759 |
0,382491 |
0,555237 |
9 |
0,711017 |
1,204263 |
2,055041 |
40 |
0,231983 |
0,34915 |
0,50313 |
10 |
0,645197 |
1,076192 |
1,795189 |
45 |
0,215372 |
0,32274 |
0,462317 |
11 |
0,593073 |
0,977119 |
1,600562 |
50 |
0,201723 |
0,301201 |
0,429388 |
12 |
0,550636 |
0,898006 |
1,449209 |
60 |
0,180468 |
0,267955 |
0,379117 |
13 |
0,515321 |
0,833255 |
1,328032 |
70 |
0,16454 |
0,243273 |
0,342256 |
14 |
0,485407 |
0,779158 |
1,228707 |
80 |
0,152056 |
0,22407 |
0,313872 |
15 |
0,459689 |
0,733212 |
1,145734 |
90 |
0,141947 |
0,208611 |
0,291173 |
16 |
0,437306 |
0,693642 |
1,075388 |
100 |
0,133553 |
0,195834 |
0,272531 |
17 |
0,417617 |
0,659166 |
1,014734 |
150 |
0,106095 |
0,154431 |
0,212848 |
18 |
0,400138 |
0,628816 |
0,961997 |
200 |
0,090434 |
0,131081 |
0,179673 |
19 |
0,3845 |
0,601863 |
0,915692 |
250 |
0,080031 |
0,115677 |
0,157986 |
