43

ристик случайной величины X , которые представляют теоретические или генеральные характеристики. Определение точности и надежности оценок будет рассматриваться далее.

Основными направлениями исследований в математической статистике являются:

•оценка неизвестных параметров и выяснение свойств этих оценок;

•проверка статистических гипотез.

4. Поговорим теперь о простейших статистических преобразованиях.

На практике мы имеем дело с числами, которые характеризуют исследуемый объект и измеряются в определенных единицах. Рассмотрим следующий пример. Фирма «Телефункен» обеспечивает телефонами-автоматами большой город. Одним из числовых признаков, характеризующих эффективность работы телефона-автомата, является количество телефонных звонков, сделанных из него за сутки. Этот числовой признак измеряется в штуках (шт).

ПримерU 3.U Собраны суточные данные по количеству звонков из 20-ти телефоновавтоматов (табл. 1):

Табл. 1. Выборка к примеру 3

Требуется проиллюстрировать на данном примере основные статистические преобразования. Расположим данные в порядке возрастания (табл. 2) значения варьирующего признака

(количества звонков):

Табл. 2. Упорядоченная выборка

Вариационным рядом называется ряд данных, расположенных в порядке возрастания варьирующего признака. Другое название вариационного ряда – упорядоченная выборка.

Взяв выборку из 20-ти данных, будет предпринята попытка судить по ним о всей генеральной совокупности (т.е. о всех телефонах-автоматах города).

При рассмотрении статистической совокупности исследователя интересует частота ni , с которой элемент (или варианта) xi встречается в выборке объёма n . Заметим, что

k

∑ni = n ,

i=1

где k – число различных вариант xi . В нашем примере 3 имеем n = 20 , k = 7 . Тогда наша выборка может быть записана в виде таблицы распределения частот (табл. 3):

Табл. 3. Таблица распределения частот

Обычно исследователя интересует также доля или частость тех или иных индивидуумов в статистической совокупности. Нас, например, будет интересовать доля телефоновавтоматов, количество звонков из которых находится в определенных границах. Так, доля телефонов-автоматов, с количеством звонков от 28 до 30 шт определяется из вариационного ряда и составляет W(28 ≤ X ≤ 30) =11/20 = 0,55 . Напомним, что выборка состоит из попав-

ших в нее значений случайной величины Х. В этой лекции вводилось понятие эмпирической функции распределения. Для нашего примера эта функция будет принимать такие значения:

F20 (26) =W ( X < 26) = 0 ; F20 (27) =W ( X < 27) =1/ 20 ; F20 (28) = 3/ 20 и т.д. Используя поня-

44

тие частоты ni можно определить частости wi , с которыми конкретные варианты xi встречается в выборке объёма n :

wi =W ( X = xi ) = ni , ∑k wi =1 . n i=1

Тогда нашу выборку из примера 3 можно записать в виде таблицы распределения частостей, оставив в ней для удобства и частоты (табл. 4):

Аналог такой таблицы в теории вероятностей – закон распределения дискретной случайной величины.

Для иллюстрации значений выборки используются графики статистических распреде-

лений: полигон, ступенчатая кривая, гистограмма.

Полигон частот строится следующим образом: а) на оси ОХ откладываются представители выборки и над ними строятся ординаты, соответствующие частотам; б) полученные т.о. точки соединяются отрезками прямой.

Рис. 1. Полигон частот, построенный по табл. 4.

Аналогом функции распределения случайной величины в математической статистике является распределение накопленных частостей (табл. 5):

Табл. 5. Таблица накопленных частостей

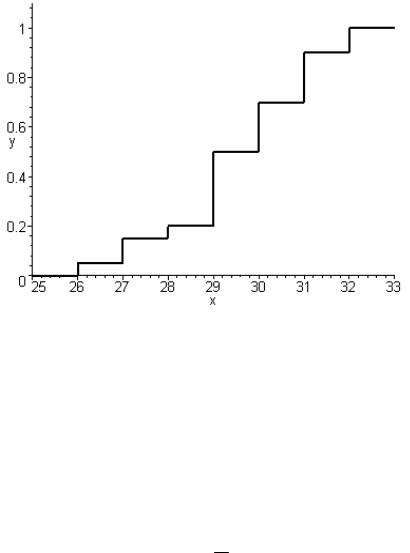
Ступенчатая кривая или кумулянта, построенная для выборочного распределения по накопленным частостям, представляет собой график эмпирической функции распределения. Ступенчатая кривая строится так: над каждым отрезком оси ОХ, изображающим расстояние между соседними представителями выборки, проводится отрезок горизонтальной прямой на

45

высоте, равной накопленной частости в данном интервале. Концы отрезков соединяются вертикальными прямыми (рис. 2). Накопленной частостью в данном интервале называется сумма всех частостей, начиная с первого интервала до данного интервала включительно.

Рис. 2. Ступенчатая кривая накопленных частостей, построенная по табл. 5.

Разность R между наибольшим и наименьшим значениями в выборке называется

размахом варьирования или широтой распределения выборки.

Для выборки из примера 3 размах варьирования равен

R = 32 − 26 = 6 .

При большом объеме n выборки и при большом числе различных значений величины X , встречающихся в выборке, приходится иногда прибегать к разбивке распределения на интервалы (разряды) значений и затем рассматривать не отдельные значения, а эти интервалы (разряды). Такой подход называют группировкой значений выборки. Обычно берут l интервалов одинаковой ширины

∆x Rl .

Далее, определяют частоты k j – количество значений выборки, попавших в j-й интервал,

причем

l

∑k j = n .

j =1

Если значение совпадает с границей интервала, то его частота делится пополам и прибавляется к частотам левого и правого интервалов. После этого подсчитываются частости интервалов wj , причем

l

∑w j =1 .

j =1

Вернемся к примеру 3. Наименьшим отрезком с целыми концами, содержащим выборку из этого примера, является отрезок [26;32]. Разобъём его на 6 интервалов с шириной

∆x =1 .

Результаты вычислений приведем в табл. 6.

46

Табл. 6. Распределение выборки из примера 3, разбитое на интервалы

Гистограмма строится следующим образом: над каждым отрезком оси ОХ , изображающим интервал значений выборки, строится прямоугольник, площадь которого равна частости или частоте в данном интервале.

Поэтому, используя таблицу 6, построим гистограмму частот выборки, разбитой на интервалы равной ширины (рис. 4).

Рис. 3. Гистограмма частот выборки, разбитой на интервалы равной ширины.

Для построения гистограммы накопленных частостей воспользуемся таблицей 7.

Гистограмма накопленных частостей (рис. 4) будет иллюстрировать эмпирическую функцию распределения выборки, разбитой на интервалы равной ширины.

47

Рис. 4. Гистограмма накопленных частостей выборки, разбитой на интервалы равной ширины.