Случаи понижения порядка

I. В случае, если дифференциальное уравнение имеет вид, гдезаданная функция. Общее решение этого уравнения можно получить произведя последовательноnинтегрирований; при каждом интегрировании будет появляться новая произвольная постоянная. Общий интеграл уравнения имеет вид

II.Уравнение

не содержащее явно и младших производных до порядкавключительно, допускает понижение порядка наединиц. Для этого выполняется замена. Тогда

сводится к нормальному уравнению

и уравнение относительно будет порядка:

.

Если найдено решение общее решение этого уравнения , то для определенияполучим уравнение. Интегрируя его, получаем общее решение исходного уравнения.

III. .Уравнение

не содержащее явно независимой переменной допускает понижение порядка на единицу путем замены обеих переменных посредством подстановки(за новую независимую переменную принимаем) с последующим выражением производныху, у, у^IV,... в соответствии с формулами

у^(IV)…

IV.ПустьF(x, u₀, u₁,..., u_n) ‑ однородная функция степениотносительно аргументовu₀, u₁,..., u_п , то есть приt  0 F(x, tu₀, tu₁,...,tu_п)= t^{k .}F(x, u₀, u₁,..., u_п). Тогда порядок “однородного” дифференциального уравненияF(x, y, y,...,y^(п))=0может быть понижен на единицу с помощью заменыу=  е, гдеz(x) ‑ новая неизвестная функция(при этому= 0 является дополнительным решением исходного однородного уравнения).

Задачи с решениями

1.Найти общее решение уравнения

Решение:Интегрируя последовательно данное уравнение, получим

Ответ:

2.

Решение:данное уравнение не содержит искомой функции и ее производных до третьего порядка включительно. Замена:

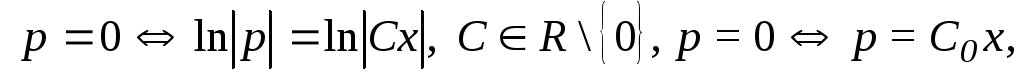
Ответ:

3..

Решение: Замена:,

Ответ: у=С₁

4. .

Решение: Функция является однородной функцией степени 2 относительно аргументов.

Замена:

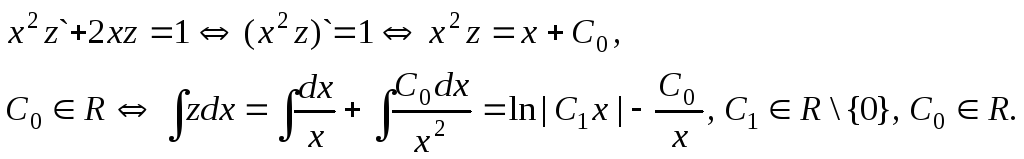
(при С₁=0 получается дополнительное решение ).

Ответ: y=C₁x

5.

Решение:

Ответ:

6.

Решение: 1 способ. Домножим наобе части данного уравнения:

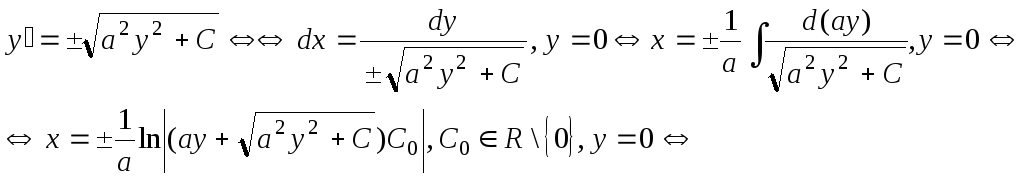
2 способ. Замена

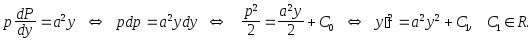
Далее преобразования те же, что в 1 способе.

3 способ. Функция является однородной функцией степени 1 относительно аргументов.

Замена:

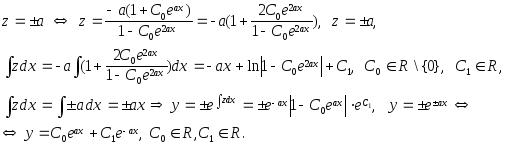
4 способ. Данное дифференциальное уравнение является линейным однородным второго порядка с постоянными коэффициентами.

Замена:

Ответ:

7.

Решение:В уравнении явно отсутствуютх и у Замена:

Ответ:

8.

Найти все частные решения, удовлетворяющие заданным начальным условиям:

Решение:

Ответ:

9.

Решение:отсутствует x в явном виде, следовательно делаем замену:

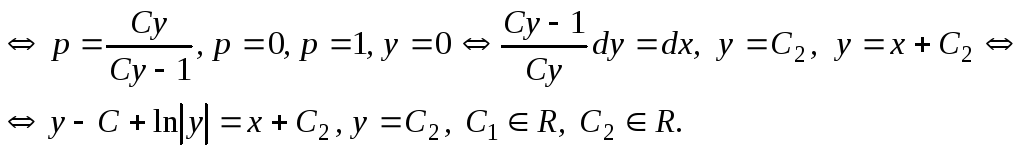Ответ:

10.

Решение:

Ответ:

11.

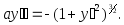
Решение:отсутствуют переменныехиу.

Замена:

Исключая параметр, найдем общий интеграл

Ответ:

12.

Решение:.

Ответ:

13.

Решение:

Получили уравнение Клеро. Замена:

1.

2. Найдем семейство особых решений:

Ответ:

14.

Решение:

Ответ:

15.

Решение:левая часть является однородной функцией аргументов

Замена:

(уравнение Бернулли)

(линейное уравнение)

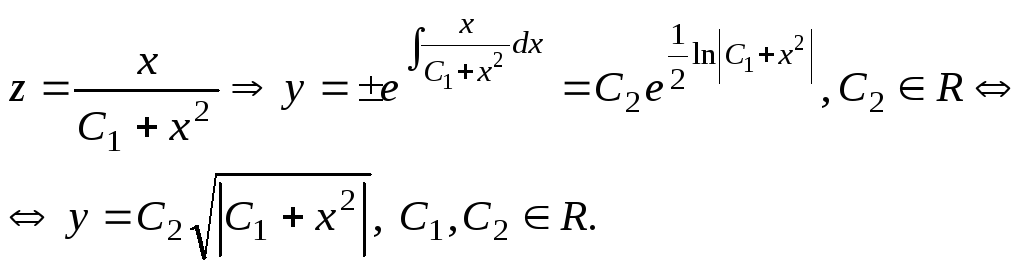
Ответ: .

Задачи для самостоятельного решения

Решить уравнения:

1.Ответ:

(Замена).

2.Ответ:

(Замена ).

3. Ответ:

4. Ответ:

5. Ответ:

6. Ответ:

7.Ответ:

8.Ответ:.

9.при,

Ответ:

10.Ответ:

- особое решение.

11.Ответ:

- особое решение.

12. Ответ:

13. Ответ:

14.Ответ:

15. Ответ:

16. Ответ:

17. Ответ:

18.Ответ:

19.приОтвет:

20.приОтвет:

21.Ответ:

22. Ответ:

23. Ответ:

24. Ответ:

25. Ответ:

26. Ответ:

27. Ответ: