
Примеры решения задач
1 Рис. 2.78. . Построить максимальный поток в сети, изображённой на рисунке 2.78, и найти разрез, пропускная способность которого равна величине потока.
Решение.
Вначале положим для всех рёбер
![]() Двигаясь от вершины
Двигаясь от вершины
![]() будем расставлять пометки (см. рис.
2.79).
будем расставлять пометки (см. рис.
2.79).
Т
Рис. 2.79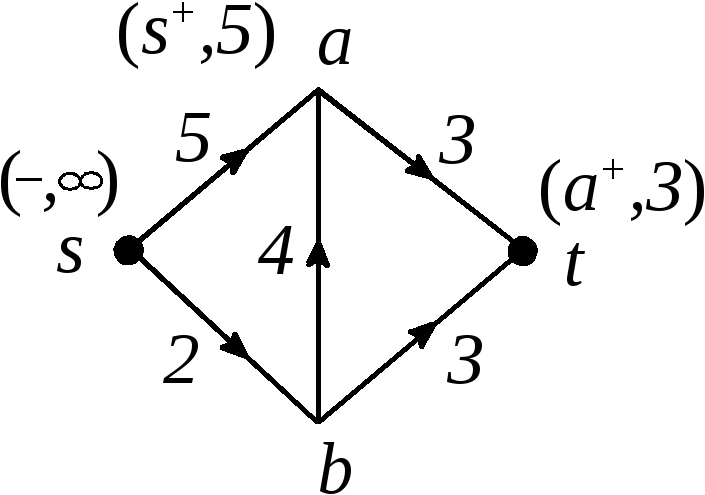
![]() оказалась помеченной, то можно величину
потока увеличить. Вдоль пути
оказалась помеченной, то можно величину
потока увеличить. Вдоль пути
![]() увеличим поток через рёбра этого пути
на
увеличим поток через рёбра этого пути
на
![]() Тогда получим распределение потока
через рёбра, изображённое на рис. 2.80.
Тогда получим распределение потока
через рёбра, изображённое на рис. 2.80.
С
Рис. 2.80
Рис. 2.81
Рис. 2.82
Рис. 2.83
![]() увеличиваем поток через рёбра на
увеличиваем поток через рёбра на
![]() (рис. 2.82). Расставляем метки ещё раз (см.
рис. 2.83). Теперь “добраться” до вершины
(рис. 2.82). Расставляем метки ещё раз (см.
рис. 2.83). Теперь “добраться” до вершины
![]() невозможно. Значит, поток является
м
невозможно. Значит, поток является
м
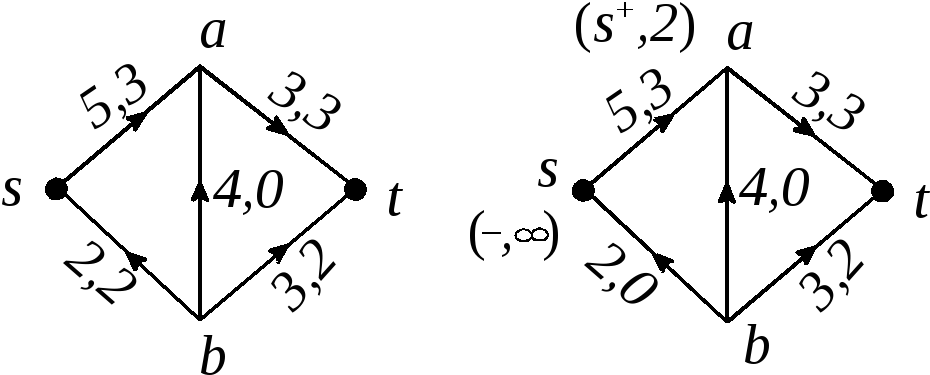
![]() Пусть
Пусть
![]() (множество вершин, до которых можно
“добраться” из
(множество вершин, до которых можно
“добраться” из
![]()
![]() оставшиеся вершины. Для разреза
оставшиеся вершины. Для разреза
![]() имеем:
имеем:
![]() Значит,
Значит,
![]()
2. Проверить, является ли поток в сети максимальным:
Р
Рис. 2.84
![]() в котором
в котором
![]() для прямых стрелок и
для прямых стрелок и
![]() для обратной стрелки, то поток не
максимальный. Его можно увеличить на
число
для обратной стрелки, то поток не
максимальный. Его можно увеличить на
число
![]()
Задачи для самостоятельного решения
1
Рис. 2.85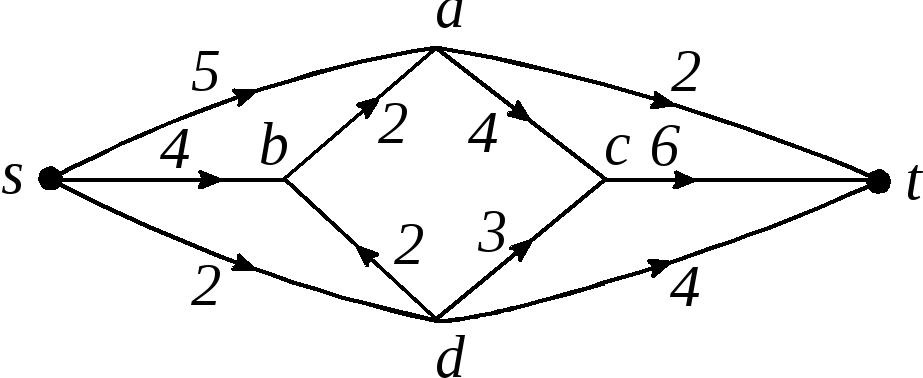
![]()
![]()
![]()
![]()
![]()
2
Рис. 2.86
Рис. 2.87

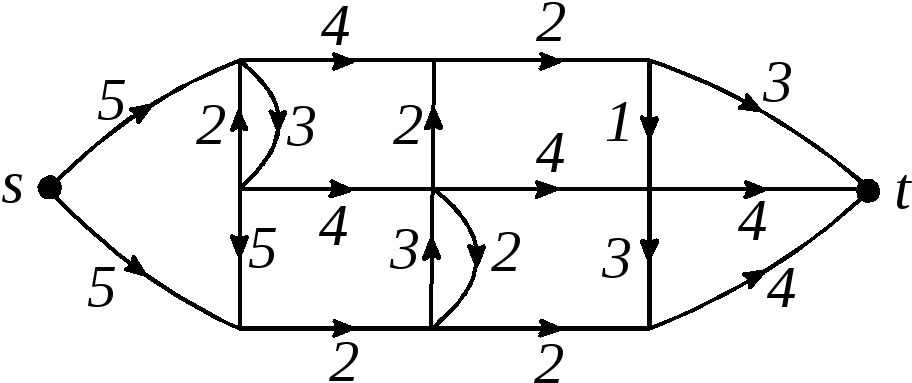
3. Найти величину максимального потока в сети:
а)
см. рис. 2.88;
Рис. 2.88
Рис. 2.89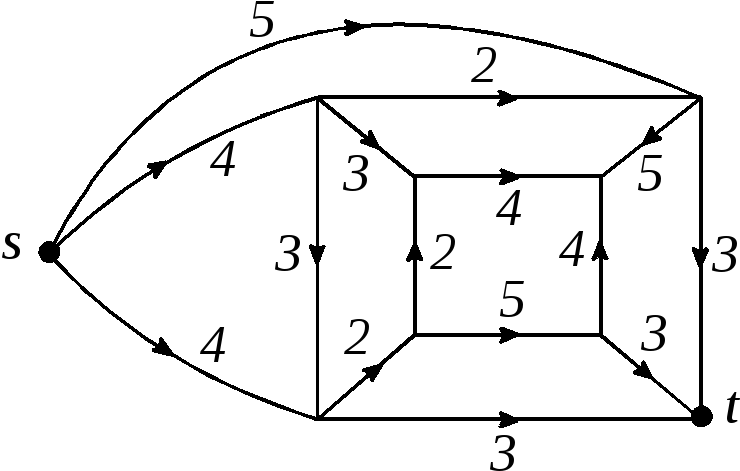
4
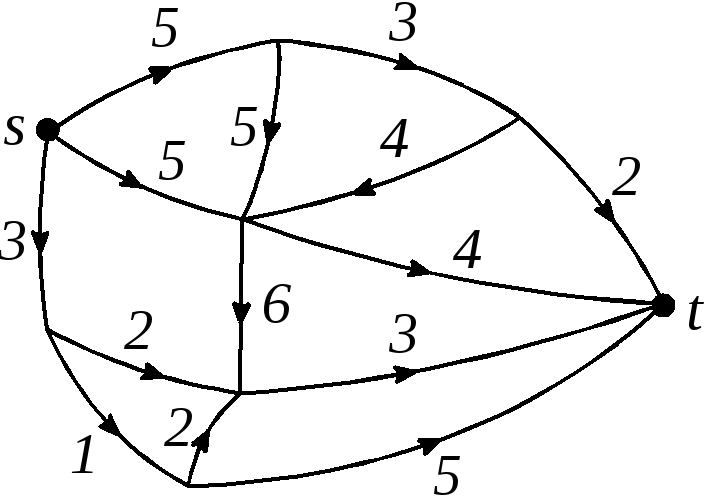
Рис. .22
Рис. 2.90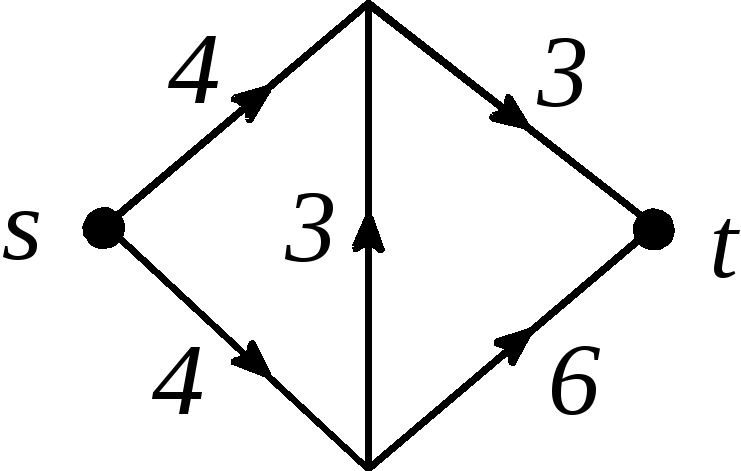
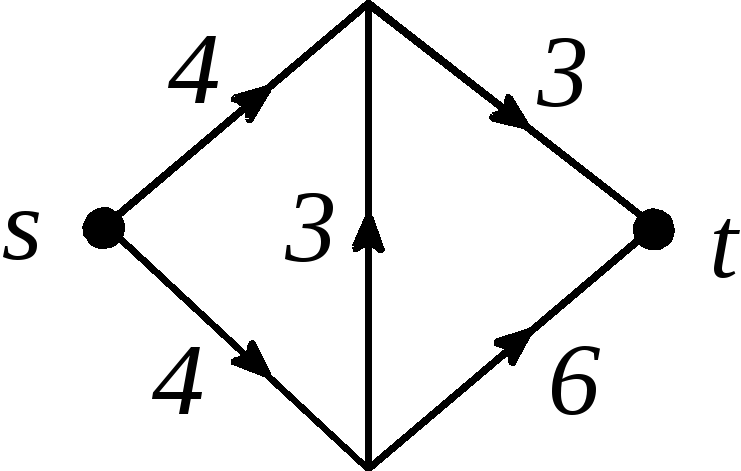
Ответы
1
Рис. 2.91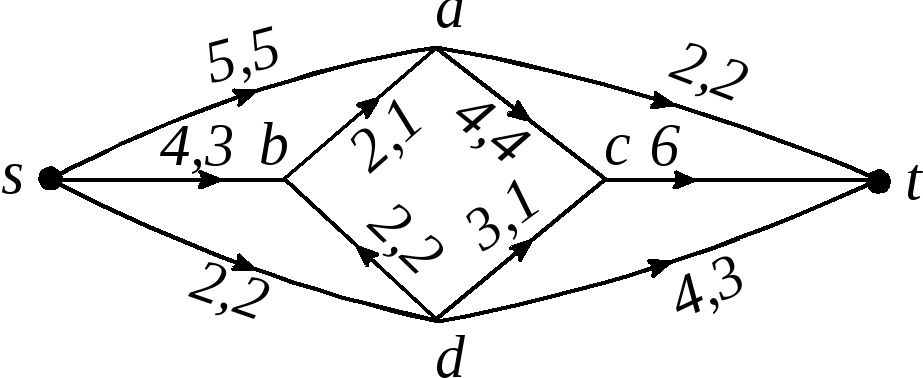
2.
а) см. рис. 2.92, разрез:
![]()
![]()
б
Рис. 2.92
Рис.2.93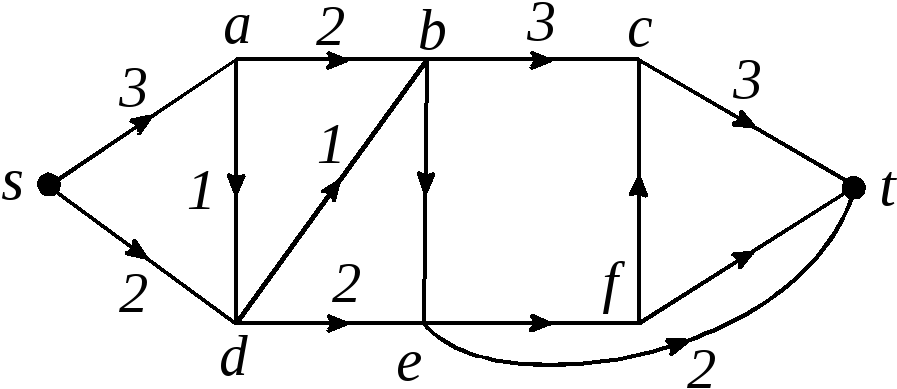
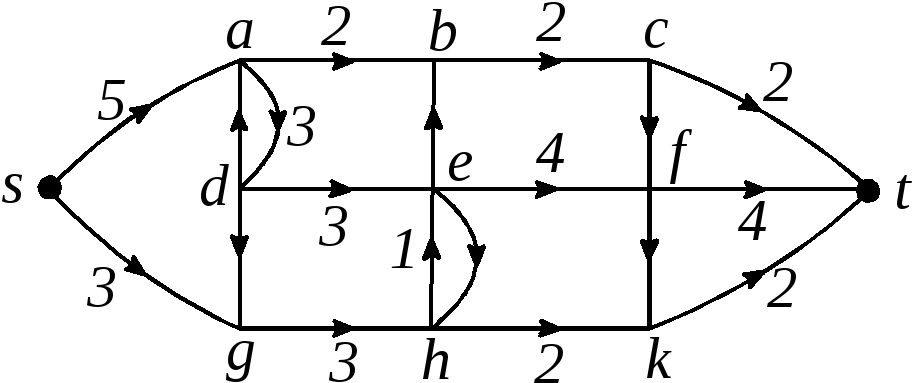
![]()
![]() (ответ неоднозначен);
(ответ неоднозначен);
3
Рис. 2.94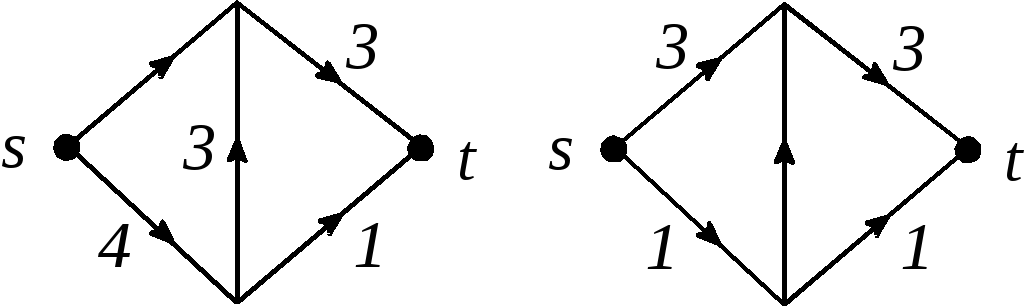
![]() б)
б)
![]() 4. См. рис. 2.94.
4. См. рис. 2.94.
