§2.5. Потоки в сетях

Транспортные, электрические, водопроводные и многие другие сети могут быть описаны на языке теории графов и с её помощью решены некоторые оптимизационные задачи.

Сеть – это ориентированный связный граф, рёбра которого помечены положительными действительными числами (для ребра идущего из вершины в вершину В графе должны быть выделены вершины (источник) и (сток). Число называется пропускной способностью ребра

В сети допускаются кратные рёбра, но не допускаются петли. Вершины сети часто называют узлами.

Поток в сети – это функция определённая для каждого ребра и удовлетворяющая условиям:

(а) для любого ребра

(б) существует число такое, что

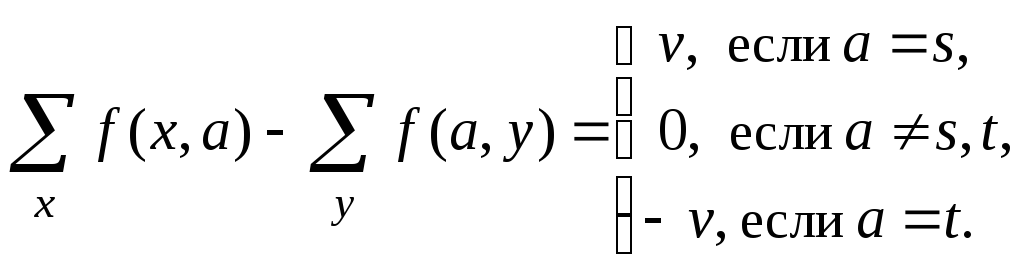
Число называется величиной потока Иногда пишут вместо чтобы подчеркнуть зависимость от Величина потока выражает количество субстанции (воды, или количества электричества, или автомашин), “перетекающих” из в за определённый промежуток времени. Равенство для внутренней точки – это “закон сохранения” (сколько единиц субстанции “втекает” в узел столько и “вытекает” из него). В математике рассматриваются и более общие сети – сети, имеющие несколько источников и несколько стоков

Поток называется максимальным, если его величина максимальна.

Основная задача теории потоков в сетях состоит в нахождении максимального потока. Мы покажем, что максимальный поток всегда существует, и приведём алгоритм его нахождения.

Теорема. В любой сети существует максимальный поток.

Доказательство. Пусть все рёбра сети. Положим Если поток, то полагаем Тогда поток можно отождествить с точкой п-мерного пространства Конечно, не всякая точка из определяет поток. Должно быть выполнено условие (а): т.е. (точка лежит в параллелепипеде ). Кроме того, должны быть выполнены условия (б): и при Например, если и сеть вблизи узла имеет вид

т

Рис. 2.71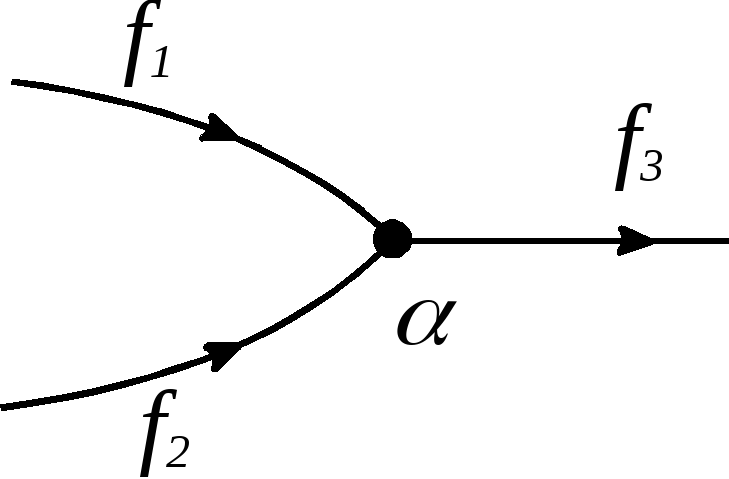

о Множество всех точек , удовлетворяющих условиям (а) и (б), таким образом, является замкнутым и ограниченным (т.е. компактом) в . Величина потока является непрерывной функцией от определённой на компакте (действительно, линейная функция; здесь ребра, выходящие из а входящие в По известной теореме математического анализа функция, непрерывная на компакте достигает своего наибольшего значения в некоторой точке из В нашем случае эта точка и будет давать максимальный поток.

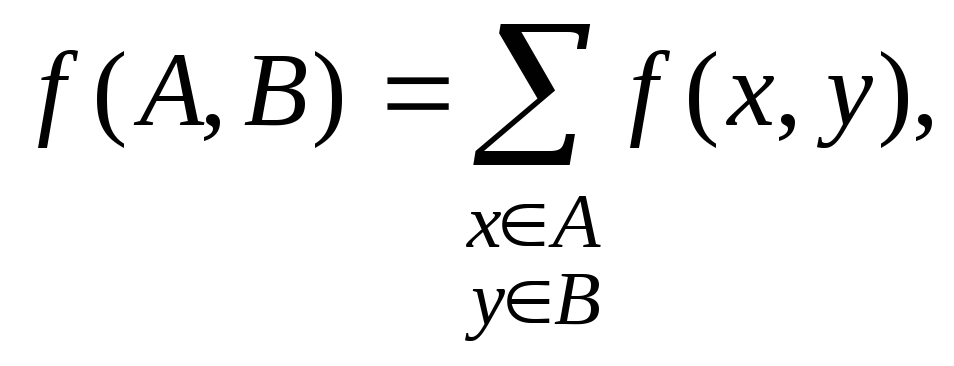
Введём ещё несколько обозначений. Пусть множество всех узлов сети. Для двух подмножеств положим 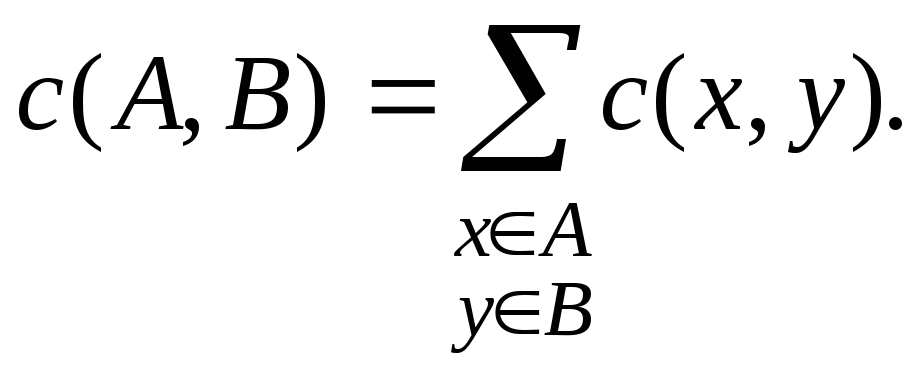Очевидно, при и аналогичное равенство имеет место для функции Введём ещё одно понятие.

Разрез – это разбиение множества всех узлов сети на два непересекающихся подмножества и причём а Число называется пропускной способностью разреза

П

Рис. 2.72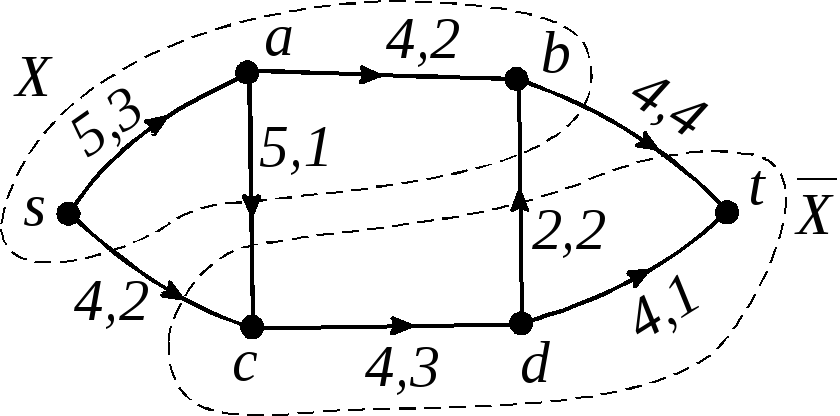

ример. В сети, изображённой на рисунке 2.72, на каждом ребре написаны числа (пропускная способность этого ребра и поток через него). В этом примере величина потока Этот поток не максимальный, так как можно, например, вдоль пути увеличить поток через рёбра на 1, условия (а) и (б) будут выполняться, но уже с Рассмотрим разрез где Его пропускная способность равна Мы имеем:

О

Рис. 2.73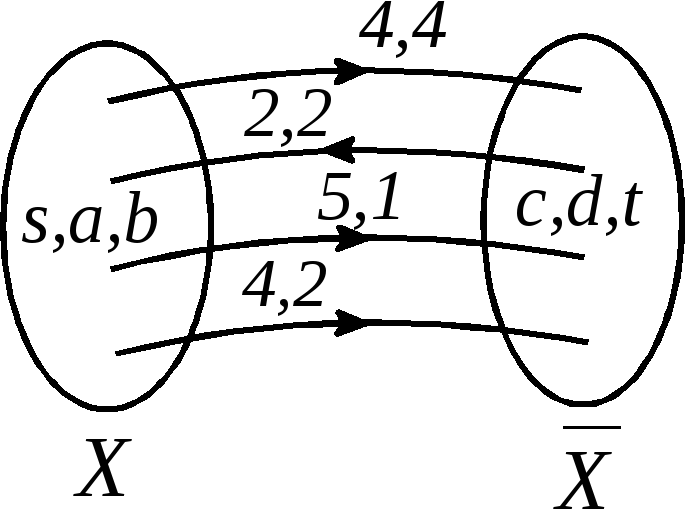

казывается, такое неравенство выполняется во всякой сети для любого потока и любого разреза. Сформулируем этот факт в виде леммы, которая потребуется затем для доказательства основной теоремы.

Лемма. Величина любого потока в сети не превосходит пропускной способности любого разреза, т.е.

Доказательство. Пусть поток и разрез. Пусть множество всех узлов сети. По определению потока имеем: при и Складывая выражения для и учитывая, что получим: Отсюда следует, что

,

так как Лемма доказана.

Итак, величина любого потока меньше или равна пропускной способности любого разреза. Поэтому, если мы найдём поток и разрез, для которых то поток будет максимальным (а разрез – минимальным). На этом простом замечании основаны алгоритм построения максимального потока и основная теорема о максимальном потоке, к изложению которых мы сейчас переходим.