3.14. Планарные графы

Напомним, что граф называется планарным, если существует правильная геометрическая реализация этого графа на плоскости. Правильные геометрические реализации планарного графа на плоскости будем называтьплоскимиграфами.

Совокупность ребер каждого простого цикла плоского графа может рассматриваться как граница некоторой области на плоскости. Те из этих областей, которые не содержат внутри себя ребер других простых циклов данного плоского графа, называютгранямиплоского графа. Отметим, что одна из граней не ограничена. Ее называютвнешнейгранью, остальные грани называютвнутреннимигранями.

Теорема 1. Пусть - плоский граф, - множество его граней. Тогда

.

Доказательство.Доказательство проведем по индукции, взяв в качестве параметра число ребер графа.

Базис индукции.Пусть, т.е. граф не имеет ребер. Тогда,, поэтому доказываемая формула справедлива.

Индуктивный переход.Предположим, что формула верна для любого графа с числом ребер меньшим либо равным. Покажем, что она остается в силе для графа, число ребер которого равно.

Рассмотрим два случая.

1. В графе имеется ребро, не являющееся мостом. Тогда оно содержится в некотором цикле и поэтому обязательно лежит на границе двух граней. Очевидно, что если удалить из графа ребро, то эти грани сольются в одну грань. Таким образом, графбудет иметьвершин,ребер, число его граней будет равно. Следовательно, по предположению индукции имеем:

.

Учтем, что (поскольку ребро- не мост). Упростив, получим:

.

2. В графе все ребра являются мостами. Тогдане имеет циклов, т.е. является лесом. Для леса выполняется равенство. Кроме того лес имеет только одну грань – внешнюю, т.е.или. Таким образом, равенствовыполняется.■

Заметим, что поскольку, то в доказанной теореме утверждается, что цикломатическое число плоского графа равно числу его внутренних граней.

Следствие 1. Пусть - плоский связный граф и - число его граней.Тогда справедлива формула Эйлера

.

Следствие 2. Граф непланарен.

Доказательство.Будем рассуждать от противного. Пусть графпланарен. Можно считать его плоским графом. Пусть- множество его граней. Посколькуне имеет петель и кратных ребер, то каждая его грань граничит не менее чем с тремя ребрами. Каждое ребро содержится в некотором цикле и, следовательно, входит в границу двух граней. Пусть, границаi-ой грани состоит изребер, где. Тогда

.

Учитывая, что , получаем:. Откуда. По следствию 1 в планарном графе, так чтоили. Графимеет 5 вершин и 10 ребер, таким образом, должно выполнять неравенство, что неверно.■

Следствие 3. Граф непланарен.

Доказательство.Будем рассуждать от противного. Пусть графпланарен. Можно считать его плоским графом. Далее будем рассуждать также как при доказательстве следствия 2. Поскольку графдвудольный, все его простые циклы имеют четную длину. Следовательно,() и, т.е.. По следствию 1, поэтому должно выполняться. Пришли к противоречию.■

Определение. Граф называется подразбиением графа , если может быть получен из графа путем последовательного применения конечного числа раз операции подразбиения ребер.

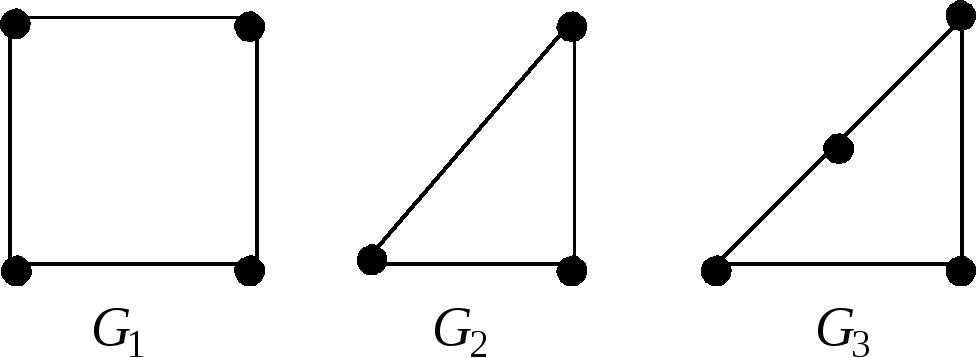Определение. Будем говорить, что графы и гомеоморфны, если существуют такие их подразбиения, которые изоморфны.

Пример 4.Граф- подразбиение графа,изоморфен графу. Следовательно, графыигомеоморфны.

Приведем без доказательства критерий планарности Понтрягина-Куратовского.

Теорема 2. Граф планарен тогда и только тогда, когда у него нет подграфов гомеморфных и .

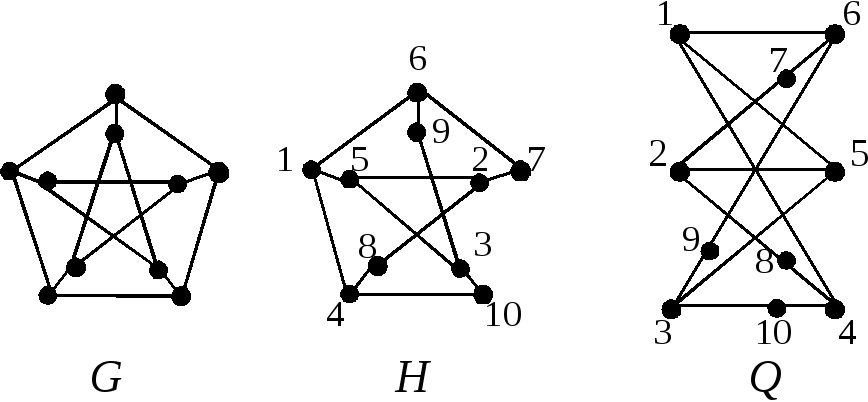
Пример 5.На рисунке изображен граф Петерсена и его подграф, а также подразбиениеграфа. Графи графизоморфны (на рисунке соответствующие вершины помечены одинаковыми числами). Следовательно, граф гомеоморфени граф Петерсена непланарен.

Теорема 3 (Хивуд, 1890). Любой планарный граф можно раскрасить не более чем пятью красками.

54