4. Статический расчет поперечной рамы

1). Расчет на постоянные нагрузки:

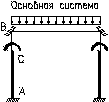
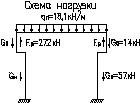
Сосредоточенный момент из-за смещения осей верхней и нижней частей колонны:

M=-(F_р+G_в)∙e₀=-(272+14)∙0,25=-71,5кН∙м

Параметры по табл. 12.4 [3]:

;

Каноническое уравнение для левого узла: r₁₁φ₁+r_1p=0

Моменты от поворота узлов на угол φ=1 (М₁):

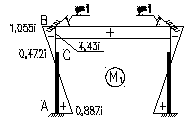
М_А=k_А∙i=0,887i;

М_С=k_С∙i=-0,472i;

М_В=k_В∙i=-1,055i;

Моменты от нагрузки на стойках М_р:

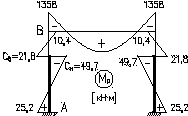
М_А=k_А∙М=0,353∙(-71,5)=-25,2кН∙м;

М_В=k_В∙М=-0,145∙(-71,5)=10,4кН∙м;

М_С^н=k_С∙М=-0,695∙(-71,5)=49,7кН∙м;

М_С^в=(k_С+1)∙М=(-0,695+1)∙(-71,5)=-21,8кН∙м;

кН∙м

Коэффициенты канонического уравнения:

r₁₁=M_B+M_B^риг=1,055i+4,43i=5,49i (по эпюре М₁);

r_1p=M_B+M_B^риг=-10,4-1358=-1368,4 (по эпюре М_р).

Угол поворота

Моменты от фактического угла поворота (М₁∙φ)

кН∙м;

кН∙м;

кН∙м;

кН∙м.

Эпюра моментов (М₁φ+М_р) от постоянной нагрузки:

М_А=221-25,2=195,8кН∙м;

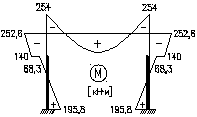
М_В=-263+10,4=-252,6кН∙м;

M_B^риг=1104-1358=-254кН∙м;

М_С^н=49,7-118=-68,3кН∙м;

М_С^в=-21,8+(-118)=-140кН∙м.

Проверкой правильности расчета служит равенство моментов в узле В (252,6≈254), равенство перепада эпюры моментов в точке С (140-68,3=71,7) внешнему моменту (71,5), а также равенство поперечных сил на верхней и нижней частях колонны.

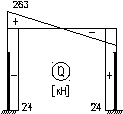
кН;кН.

Разница (7,5%) получена в результате округления параметра α (0,283≈0,3).

2). Расчет на нагрузку от снега:

Сосредоточенный момент на колонне:

M=F_p∙e₀=-875,5∙0,25=-218,9кН∙м

Моменты от нагрузки (М_р):

М_А=0,353∙(-218,9)=-77,3кН∙м;

М_В=-0,145∙(-218,9)=31,7кН∙м;

М_С^н=-0,695∙(-218,9)=152кН∙м;

М_С^в=0,305∙(-218,9)=-67кН∙м;

кН∙м

Коэффициенты канонического уравнения:

r₁₁=M_B+M_B^риг=5,49i;

r_1p=M_B+M_B^риг=-31,7-4377,8=-4410.

Угол поворота

Моменты от фактического угла поворота (М₁∙φ)

кН∙м;

кН∙м;

кН∙м;

кН∙м.

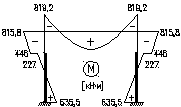
Эпюра моментов (М₁φ+М_р) от снеговой нагрузки:

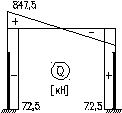
М_А=712,5-77,3=635,5кН∙м;

М_В=-847,5+31,7=-815,8кН∙м;

М_С^в=-379-67=-446кН∙м.

М_С^н=-379+152=-227кН∙м;

M_B^риг=3558,6-4377,8=-819,2кН∙м.

Поперечная сила:

кН

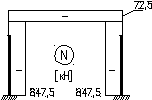
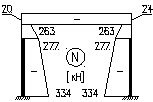
Продольная сила:

N_B =N_A= -847,5кН

N_риг= -72,5кН

3). Расчет на вертикальную нагрузку от мостовых кранов:

Расчет проводится при расположении тележки крана у левой стойки.

Основная система и схема нагрузки:

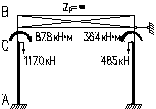
Проверка возможности считать ригель абсолютно жестким:

;;; (12.1[3]).

;.

Каноническое уравнение для определения смещения плоской рамы:

r₁₁Δ+r_1p=0

Моменты и реакции от смещения верхних узлов на Δ=1 (по табл. 12.4 [3]):

Моменты и реакции на левой стойке от нагрузки:

М_А=k_А∙М=0,353∙878=310кН∙м;

М_В=k_В∙М=-0,145∙878=-127кН∙м;

М_С^н=k_С∙М=-0,695∙878=-610кН∙м;

М_С^в=(k_С+1)∙М=0,305∙878=268кН∙м;

кН∙м

Усилия на правой стойке получим, умножая усилия левой стойки на отношение:

М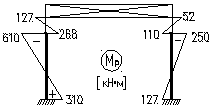оменты на правой стойке:

М_А=310∙0,41=127кН∙м;

М_В=-127∙0,41=-52кН∙м;

М_С^н=-610∙0,41=-250кН∙м;

М_С^в=268∙0,41=110кН∙м;

Реакция верхних концов стоек:

r_1p=F_pB-F_pB^пр=F_pB– (F_pB∙0,41)=79,3-79,3∙0,41=46,8кН

Смещение плоской рамы:

Учет пространственной работы каркаса:

α_пр– коэфф. пространственной работы.

Крановая нагрузка местная, поэтому α_пр≠1

При жесткой кровле по формуле 12.21 [3]:

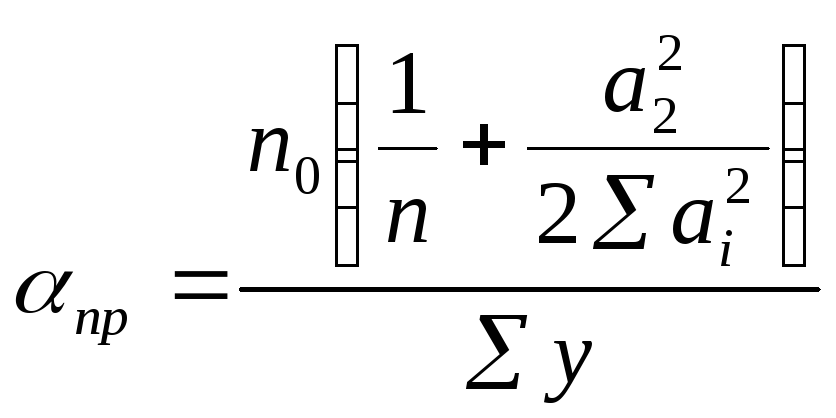, где

n₀=4 – число колес кранов на одной нитке подкрановых балок;

n=8 – число рам в блоке;

а_i = 12, 36, 60, 84м – расстояния между симметрично расположенными относительно середины блока рамами;

а₂= 60м – вторыми от торцов;

∑y=2,94м – сумма ординат линии влияния реакции рассматриваемой рамы.

Смещение с учетом пространственной работы:

Δ_пр= α_пр∙Δ, (12.13[3])

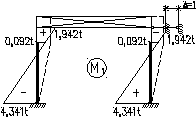
Эпюра моментов от M₁∙Δ_прот фактического смещения рамы с учетом пространственной работы:

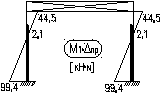
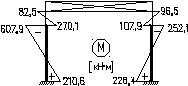
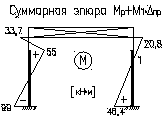
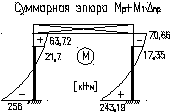
Суммарная эпюра M_p+M₁∙Δ_пр

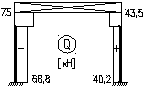
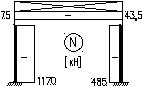
Поперечная сила Q:

Левая стойка:

кН;кН.

Правая стойка:

кН;кН.

4). Расчет на горизонтальные воздействия мостовых кранов:

Основная система, эпюра М₁, каноническое уравнение, коэфф. α_пр– такие же, как при расчете на вертикальную нагрузку от мостовых кранов.

Моменты и реакции в основной системе от силы Т:

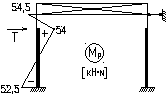
М_А=k_A∙T∙H=-0,102∙31∙16,6=-52,5кН∙м;

М_В=k_B∙T∙H=-0,106∙31∙16,6=-54,5кН∙м;

М_С=k_C∙T∙H=0,105∙31∙16,6=54кН∙м;

F_pB= k’_B∙T=0,704∙31=21,8кН.

Смещение верхних концов с учетом пространственной работы:

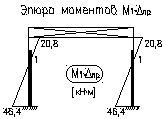
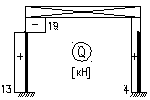
Поперечная сила Q:

кН;

кН;

кН.

Проверка правильности решения – скачек на эпюре Q19+13=32кН ≈ Т

5). Расчет на ветровую нагрузку:

Основная система и эпюра М₁– как для крановых воздействий.

Эпюра М_рна левой стойке:

М_А=k_A∙q_э∙H²=-0,104∙1,8∙16,6²=-51,58кН∙м;

М_В=k_B∙q_э∙H²=-0,056∙1,8∙16,6²=-27,78кН∙м;

М_С=k_C∙q_э∙H²=0,35∙1,8∙16,6²=17,36кН∙м;

F_pB=k’_B∙q_э∙H=0,452∙1,8∙16,6=13,51кН.

На правой стойке усилия получаются умножением на коэфф.:

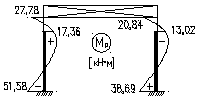
М_А=-51,58∙0,75=-38,69кН∙м;

М_В=-27,78∙0,75=-20,84кН∙м;

М_С=17,36∙0,75=13,02кН∙м;

Коэффициенты канонического уравнения:

r₁₁=-0,757t, (12.22 [3])

r_1p=F_pB+F_pB’+F_B+F_B’=13,51+10,13+6,85+5,14=35,63

Смещение рамы (ветровая нагрузка воздействует на все рамы блока и поэтому α_пр=1):

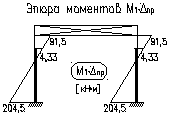
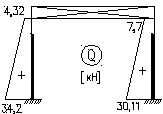
Эпюра Qна левой стойке:

кН

кН

На правой стойке:

кН

кН

При правильном решении сумма поперечных сил внизу должна быть равна сумме всех горизонтальных нагрузок:

Q_A+Q_A^пр=34,2+30,11=64,31кН

(q_э-q_э’)∙H+F_B+F_B’=(1,8+1,35)∙16,6+6,85+5,14=64,28кН

64,31 ≈ 64,28

Q_B+Q_B^пр=4,32+7,7=12,02кН

F_B+F_B’=6,85+5,14=11,99кН

12,02 ≈ 11,99