2. Алгоритм Евклида

Вычисление НОД.

Число а называется общим делителем чисел b₁, b₂,…, b_n, если оно является делителем каждого из чисел b₁, b₂,…, b_n.

Наибольшим общим делителем целых чисел a₁,…,a_n , называется такой их общий делитель, который делится на любой общий делитель этих чисел: обозначается НОД (a₁,…,a_n).

Каноническое разложение

Если a=и b= суть канонического разложения целых положительных чисел a и b, то d=НОД(a,b), где d=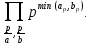

Простой способ

a= 24 b=6

24-6=18

18-6=12

12-6=6 < НОД

6-6=0

Теорема Евклида.

Теорема Евклида

Пусть a и b – два целых числа, b ≠ 0 и a = bq + r (0 ≤ r < |b|). Тогда НОД (a,b) = НОД (b,r).

Алгоритм Евклида, сравнение алгоритмов.

Для нахождения НОД двух целых чисел применяется способ «последовательного деления», называемый алгоритмом Евклида.

Сущность алгоритма Евклида состоит в том, что в силу теоремы Евклида задача нахождения НОД (a,b) сводится к более простой задаче нахождения НОД (b,r), 0 ≤ r < |b|. Если r = 0, то НОД (a,b) = b. Если же r ≠ 0, то получаем цепочку неравенств

a = bq₀ + r₁, 0 ≤ r < |b|,

b = r₁q₁ + r₂, 0 ≤ r₂ < r₁,

……………………

r_n-2 – r_n-1q_n-1 + r_n, 0≤ r_n < r_n-1,

r_n-1 = r_nq_n + r_n+1.

Приходим к выводу: если к целым числам a,b, где b ≠ 0, применить алгоритм Евклида, то последний ненулевой остаток в этом алгоритме и есть НОД (a,b).

Пример: a=86, b=32

a = b*q + p₁

86 = 32*2 + 22

32 = 22*1 + 10

22 = 10*2 +2

10 = 2*5 + 0

Ответ: НОД (86, 32) = 2

Сравнение алгоритмов

Сравним «простой» алгоритм и алгоритм Евклида. Для малых чисел ни один из них не дает преимущества в вычислениях, но для больших параметров эффективней применять алгоритм Евклида.

Соотношение Безу.

(Целые числа называют взаимно простыми, если любой их общий делитель равен +1 или -1.)

Теорема. Если целые числа a и b взаимно простые, то существуют целые числа u и v такие, что au+bv=1.

Доказательство. Рассмотрим множество I = {ax + by | x,y ϵ Z}. a ϵ I, так как a = a*1 + b*0, и b ϵ I, так как b = a*0 + b*1. Обозначим через d наименьшее положительное натуральное число, принадлежащее множеству I. Так как d ϵ I, то, согласно определению множества I, существуют целые числа u и v такие, что au+bv=d; a, b ϵ I, значит, d – общий делитель чисел a, b. Но a, b – взаимно простые, d > 0, значит, d = 1 и au+bv = 1.

Пример. Пусть a = 5 и b = 7, тогда u = -4 и v = 3, т.е. 5*(-4) + 7*3 = 1.

Расширенный алгоритм Евклида.

Алгоритм, примененный к паре чисел a,b порождает последовательность такую, что

r_i-1=r_iq_i+r_i+1 для 1≤i≤n, где r₀=a, r₁=b, r_n+1=0.

Из этих формул легко получается рекуррентная последовательность:

из которой теперь следует классический результат

r_n=НОД(a,b)=u_na+v_nb.

Литература: [1], [3], [5].

3. Модулярная арифметика

Модулярное исчисление состоит в осуществлении нескольких малых вычислений по модулям простых чисел и получении необходимого результата с помощью теоремы об остатках.

Китайская теореме об остатках.

Пусть n₁ ,n₂, …, n_r - попарно взаимно простые числа. Пусть а₁ ,а₂, …, а_r произвольно целые числа. Тогда система

имеет по крайней мере одно решение. Кроме того, если х' – другое решение этой системы, то хºх'(mod n₁·n₂· …·n_r ).

Смешанная система счисления.

Идея, принадлежавшая Л.Гарнеру и представленная у Д.Кнута, состоит в том, чтобы связать с модулярным представлением еще одно представление, называемое смешанной системой счисления.

Основанием смешанной системы счисления называется множество из r³2 целых чисел n₁,n₂,…,n_r, не обязательно взаимно простых. Если положим иn=n₁·n₂·…·n_r, то имеется биекция (взаимно однозначное соответствие):

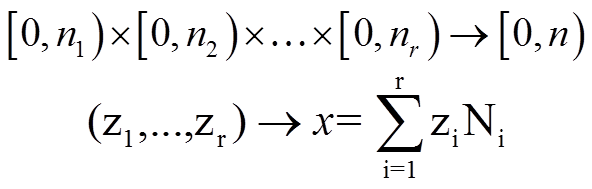
Обратное отображение определяется при помощи евклидовых делений:

x=q₁n₁+z₁, q₁= q₂n₂+z₂, … , q_r-1= q_rn_r+z_r.

В случае, когда все числа n_i равны, получаем обычную позиционную систему счисления (смешанная система счисления, следовательно, это система, в которой основания варьируется).

Формулы определения цифр.

Пусть n₁,n₂,…,n_r – попарно взаимно простые числа. Пусть 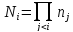иC_i – обратные к N_i по модулю n_i.

Рассмотрим целое число x, модулярные компоненты которого x₁,x₂,…,x_r тогда цифры x в системе со смешанным основанием n_i обозначим через z_i ; они находятся по формулам:

z₁= x₁mod n₁,

z₂= C₂(x₂-z₁) mod n₂,

z₃= C₃(x₃-(N₂z₂+z₂)) mod n₃,

……………

z_r= C_r(x_r-(N_r-1z_r-1+…+ N₂z₂+z₁)) mod n_r.

Чтобы осуществить обратный переход от системы со смешанным основанием к модулярному представлению, достаточно провести следующие вычисления:

x₁=z₁,

x₂=(z₁+z₂n₁)mod n₂,

x₃=(z₁+z₂n₁+z₃n₁n₂)mod n₃,

…

x_r=(z₁+z₂n₁+…+z_rn₁n₂…n_r-1)mod n_r.

Сравнение чисел, определение цифр в позиционной системе счисления.

Пусть имеются два целых числа x и x', заданные своими модулярными компонентами, и мы хотели узнать, которое из этих чисел (можем считать, что они оба лежат в [0,m)) больше, по возможности не вычисляя явный вид этих чисел. Вычислим сначала цифры z_i и z_i', соответствующие x и x' в смешанной системе счисления, определяемой модулями. В этом случае x<x' тогда и только тогда, когда наибольший вес i, на котором различаются эти числа, таков, что z_i<z_i'.

Определение цифр в позиционной системе счисления

Пусть целое х задано модулярными компонентами. Мы хотим вычислить его цифры в системе с основанием b. По схеме Горнера

x mod b(…((z_r mod)·n_r-1+ z_n-1 mod b)…)·n₁+z₁ mod b (x-(x mod b))/b

Так мы получили первую цифру x в системе счисления с основанием b.

Алгоритм умножения двух чисел?

Литература: [1], [4], [5].