Основные понятия, определения и законы молекулярной физики и термодинамики

Молекулярная физика – раздел физики, в котором изучаются физические свойства и строение вещества в различных агрегатных состояниях на основе их микроскопического (молекулярного) строения.

Молекулярно-кинетическая теория строения вещества – раздел молекулярной физики, в котором изучаются свойства тел на основе представлений об их молекулярном строении.

Статистическая физика – раздел молекулярной физики, в котором изучаются свойства и движения не отдельных молекул (частиц), а совокупности частиц, характеризующихся средними величинами.

Термодинамика – наука, в которой изучаются свойства физических систем вне связи с их микроскопическим строением.

Молекула – наименьшая часть вещества, обладающая его основными химическими свойствами и состоящая из атомов, соединенных между собой химическими связями.

Атом – наименьшая частица химического элемента (микрочастица), обладающая его свойствами. Атомы в разных сочетаниях входят в состав молекул разных веществ.

Относительная атомная масса – отношение массы данного атома к 1/12 массы изотопа углерода с массовым числом 12 (¹²С).

Относительная молекулярная масса – отношение массы данной молекулы к 1/12 массы атома ¹²С.

Моль – количество вещества, в котором содержится число частиц, равное числу атомов в 0,012 кг изотопа углерода С¹².

Число Авогадро – число атомов или молекул в моле любого вещества: N_А = 6,0210²³ моль^-1.

Молярная масса – масса вещества, взятого в количестве одного моля:

 = m₀N_А.

Идеальный газ – теоретическая модель газа, в которой не учитывается взаимодействие его частиц (средняя кинетическая энергия частиц много больше энергии их взаимодействия). Размеры молекул идеального газа малы по сравнению с расстояниями между ними. Суммарный собственный объем молекул такого газа мал по сравнению с объемом сосуда. Силы взаимодействия между молекулами настолько малы, что движение молекул от столкновения до столкновения происходит по прямолинейным отрезкам. Число ежесекундных столкновений молекул велико.

Основные положения молекулярно-кинетической теории идеального газа:

1) газ состоит из мельчайших частиц – атомов или молекул, находящихся в непрерывном движении;

2) в любом, даже очень малом объёме, к которому применимы выводы молекулярно–кинетической теории, число молекул очень велико;

3) размеры молекул малы по сравнению с расстояниями между ними;

4) молекулы газа свободно движутся между двумя последовательными взаимодействиями друг с другом или со стенками сосуда, в котором он находится. Силы взаимодействия между молекулами, кроме моментов соударения, пренебрежимо малы. Соударения молекул происходят без потерь механической энергии, т.е. по закону абсолютно упругого взаимодействия;

5) при отсутствии внешних сил молекулы газа распределяются равномерно по всему объёму;

6) направления и значения скоростей молекул газа самые различные.

Основное уравнение молекулярно-кинетической теории газов:

,

где – средняя квадратичная скорость.

Основное уравнение молекулярно-кинетической теории газов для давления:

, или ,

где n₀ – N^'/V – число молекул в единице объема;

–средняя кинетическая энергия поступательного движения молекул газа;

k – постоянная Больцмана.

Закон Авогадро: «В одинаковых объемах при одинаковых температурах и давлениях содержатся одинаковые количества молекул».

Закон Дальтона: «Давление смеси газов равно сумме парциальных давлений, т.е. тех давлений, которые имел бы каждый из входящих в смесь газов, если бы в объеме, занятом смесью, находился он один»:

.

Уравнение состояния идеальных газов для произвольной массы m (уравнение Менделева–Клапейрона):

,

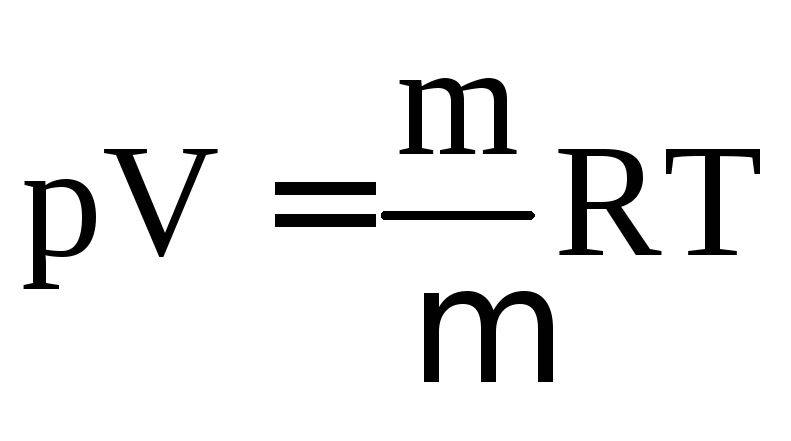где R – газовая постоянная, которая численно равна работе расширения одного моля газа при его нагревании на один градус в условиях постоянного давления;

T – абсолютная температура.

Степени свободы i – число независимых координат, необходимых для полного описания положения системы в пространстве. Все степени свободы равноправны.

Общее число степеней свободы

где – число степеней свободы поступательного движения;

–число степеней свободы вращательного движения;

–число степеней свободы колебательного движения;

i_кп – число степеней свободы колебаний точки при поступательном движении;

i_квр – число степеней свободы колебаний точки при вращательном движении.

Молекулы газа имеют число степеней свободы:

а) одноатомная – i = 3 (три степени свободы поступательного движения);

б) двухатомная при упругой связи между атомами – i = 6;

в) двухатомная при жёсткой связи между атомами – i = 5;

г) трёхатомная молекула при жёсткой связи между атомами – i = 6.

Теорема о равномерном распределении энергии по степеням свободы: «На любую степень свободы приходится в среднем одинаковая энергия, равная ». Молекула, обладающая i степенями свободы, обладает энергией

где i = i_п + i_вр + i_к.

Внутренняя энергия произвольной массы газа m равна сумме из энергий отдельных молекул:

,

где  – молярная масса газа.

Теплоемкость – физическая величина, численно равная количеству теплоты, которое необходимо сообщить веществу для нагревания его на один градус.

Удельная теплоёмкость (c) – физическая величина, численно равная количеству теплоты, которое необходимо сообщить единице массы вещества для нагревания её на один градус.

Молярная теплоёмкость (C) – физическая величина, численно равная количеству теплоты, которое необходимо сообщить одному молю вещества, чтобы увеличить его температуру на один градус:

.

Удельная теплоёмкость при постоянном объеме (c_v) – физическая величина, численно равная количеству теплоты, которое необходимо сообщить единице массы вещества для нагревания её на один градус в условиях постоянного объема:

Удельная теплоёмкость при постоянном давлении (c_p) – физическая величина, численно равная количеству теплоты, которое необходимо сообщить единице массы вещества для нагревания её на один градус в условиях постоянного давления:

.

Молярная теплоёмкость при постоянном объеме (C_v) – физическая величина, численно равная количеству теплоты, которое необходимо сообщить одному молю вещества, чтобы увеличить его температуру на один градус в условиях постоянного объема:

. .

Молярная теплоёмкость при постоянном давлении (C_p) – физическая величина, численно равная количеству теплоты, которое необходимо сообщить одному молю вещества, чтобы увеличить его температуру на один градус в условиях постоянного давления:

, .

Отношение молярных и удельных теплоемкостей :

Система – совокупность рассматриваемых тел (в частности, молекул, атомов, частиц).

Параметры состояния системы: p – давление, V – объём, T – температура:

а) интенсивные параметры – параметры (давление, температура, концентрация и др.), не зависящие от массы системы.

Температура – физическая величина, характеризующая состояние термодинамического равновесия макроскопической системы. Свойство температуры – определять направление теплового обмена. Температура в молекулярной физике определяет распределение частиц по уровням энергии и распределение частиц по скоростям.

Термодинамическая температурная шкала – температурная шкала, определяемая температура (абсолютная температура) в которой всегда положительна;

б) экстенсивные параметры – параметры (объем, внутренняя энергия, энтропия и др.), значения которых пропорциональны массе термодинамической системы или ее объему.

Внутренняя энергия системы – суммарная кинетическая энергия хаотического движения молекул, потенциальная энергия их взаимодействия и внутримолекулярная энергия, т.е. энергия системы без учёта кинетической энергии её в целом (при движении) и потенциальной энергии во внешнем поле.

Изменение внутренней энергии при переходе системы из состояния в состояние равно разности значений внутренней энергии в этих состояниях и не зависит от пути перехода системы из одного состояния в другое.

Уравнение состояния системы:

F(p,V,T) = 0.

Неравновесное состояние системы – такое, при котором какой–либо из ее параметров состояния системы изменяется.

Равновесное состояние системы – такое, при котором все параметры состояния системы имеют определённые значения, постоянные при неизменных внешних условиях.

Время релаксации – время, в течение которого система приходит в равновесное состояние.

Процесс – переход системы из одного состояния в другое состояние, связанный с изменением хотя бы одного из ее параметров состояния:

а) обратимый процесс – процесс, при котором возможно осуществить обратный переход системы из конечного в начальное состояние через те же промежуточные состояния так, чтобы не осталось никаких изменений в окружающей систему среде;

б) необратимый процесс – процесс, при котором невозможно осуществить обратный переход системы в первоначальное состояние, или если по окончании процесса в окружающей среде или в самой системе произошли какие-либо изменения;

в) круговой процесс (цикл) – такая последовательность превращений, в результате которой система, выйдя из какого-либо исходного состояния, возвращается в него вновь. Любой круговой процесс состоит из процессов расширения и сжатия. Процесс расширения сопровождается работой, совершаемой системой, а процесс сжатия – работой, совершаемой над системой внешними силами. Разность этих работ равна работе данного цикла.

Динамические закономерности – закономерности, подчиняющиеся системам уравнений (в том числе дифференциальных, интегральных и др.), допускающих существование единственного решения для каждого начального условия.