Энергия, работа, мощность. Законы сохранения в механике

Энергия – количественная мера и качественная характеристика движения и взаимодействия материи во всех ее превращениях. Она является функцией состояния системы и характеризует способности системы к совершению работы при переходе из одного состояния в другое.

Изменение энергии при переходе системы из одного состояния в другоеравно работе, совершаемой системой в процессе перехода:

W = W₁ – W₂ = A.

Диссипация (рассеяние) энергии механических систем – процесс перехода части их механической энергии в другие формы под влиянием внешних факторов (например, за счет наличия сил сопротивления).

Диссипативные системы – системы, в которых полная механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы, например в теплоту.

Механическая энергия – физическая величина, равная работе, которая может быть произведена при полном превращении движения данной формы в механическую форму движения материи.

Кинетическая энергия - физическая величина, характеризующая способность движущегося тела или системы совершать работу при торможении до полной остановки – одна из функций состояния ее движения:

.

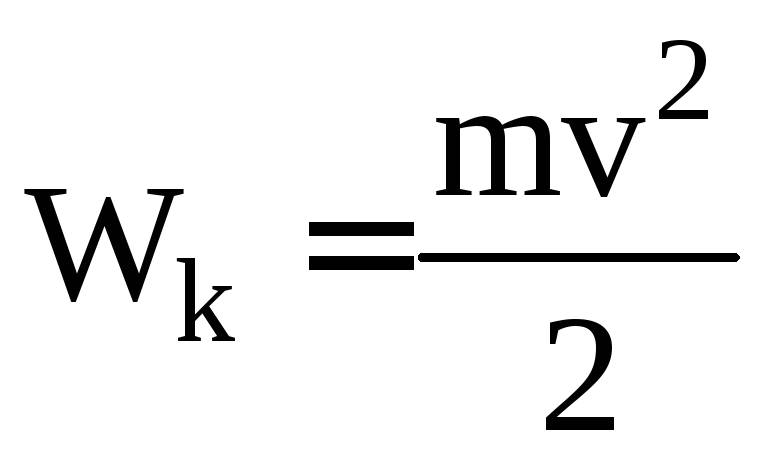Кинетическая энергия системы –сумма кинетических энергий отдельных тел (материальных точек) этой системы:

,

где – масса тела (системы);

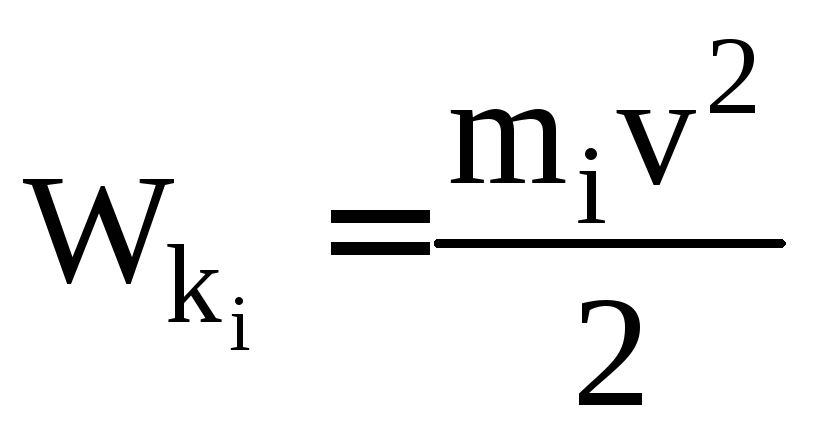–кинетическая энергия i-го тела системы.

Связь между кинетической энергией тела (системы) и его импульсом:

.

Кинетическая энергия при вращательном движении:

1) элементарной массы m_i:

,

где I_i = m_i∙r_i² – момент инерции материальной точки, относительно выбранной оси вращения;

2) тела (системы):

,

где – момент инерции тела относительно той же оси вращения.

Потенциальная энергия – физическая величина, характеризующая способность системы совершать работу, связанную с изменением конфигурации и взаимного расположения тел или частей в системе.

Изменение потенциальной энергии системы зависит только от начального и конечного ее состояний и равно работе внутренних (консервативных) сил системы, взятой с обратным знаком:

dW_p = –dA.

Характеристики поля тяготения –напряженность и потенциал поля тяготения.

Напряженностью поля тяготения в данной точке называется векторная физическая величина, равная по величине и направлению силе, действующей на единичную массу, помещенную в данную точку поля:

.

Потенциалом поля тяготения называют скалярную физическую величину, равную потенциальной энергии единичной массы, помещенной в данную точку поля:

,

т.е. потенциал поля тяготения тоже с увеличением расстояния увеличивается и при r   равен нулю.

Связь между напряженностью и потенциалом поля тяготения:

.

В общем случае связь между напряженностью и потенциалом поля тяготения выражается соотношением

g = -grad.

Потенциальная энергия тяготеющих масс

.

Потенциальная энергия системы «тело – Земля», если тело находится на некоторой высоте h над поверхностью Земли:

,

где – потенциальная энергия системы «тело – Земля», если тело находится на поверхности Земли.

Изменение потенциальной энергии в том случае, когда тело поднимается на некоторую высоту h над поверхностью Земли:

.

Потенциальная энергия упругой деформации

.

Связь потенциальной энергии материальной точки (тела, системы) во внешнем силовом поле с силой, действующей на материальную точку (тело, систему):

dWp = –F_rdr, .

В векторной форме

,

где W_p = f (x,y,z) – потенциальная энергия системы.

Признак устойчивого равновесия (положения) системы – минимум потенциальной энергии:

; .

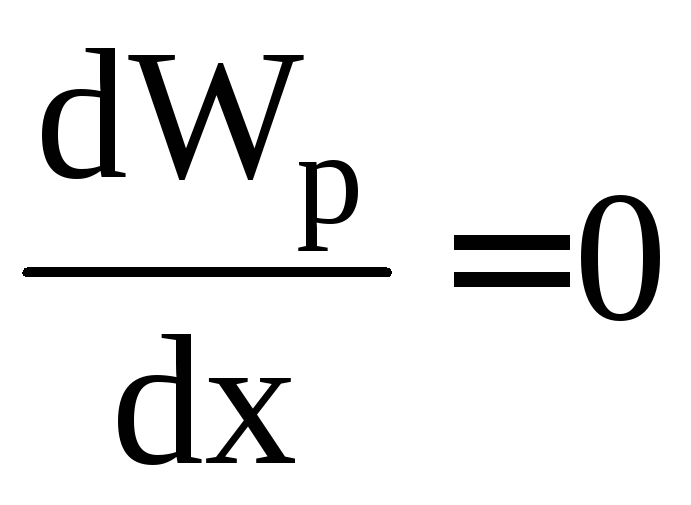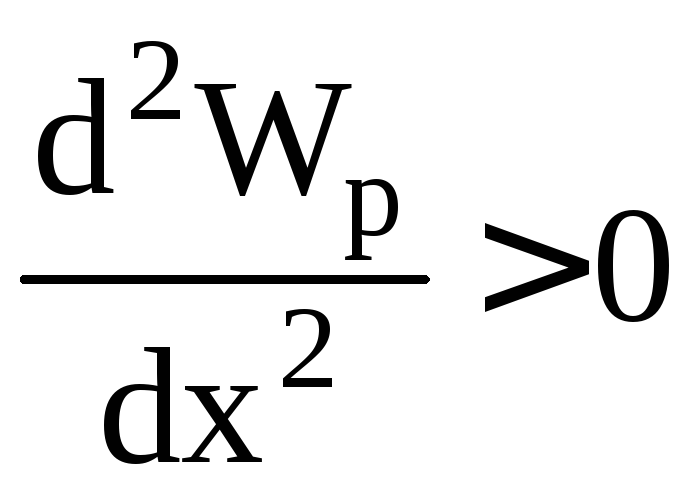Внутренняя энергия – энергия физической системы, зависящая от ее внутреннего состояния; сумма кинетической энергии хаотического (теплового) движения всех микрочастиц системы, энергии взаимодействия этих частиц и внутримолекулярной энергии.

Изменение внутренней энергии системы при ее переходе из состояния в состояние:

U = U₂ – U₁,

где U₁ – внутренняя энергия системы в начальном состоянии;

U₂ – внутренняя энергия системы в конечном состоянии.

Изменение внутренней энергии системы, выполняющей замкнутый процесс:

U = 0.

Полная механическая энергия системы, совершающей гармоническое колебательное движение,– это сумма потенциальной и кинетической энергий.

Потенциальная энергия системы, совершающей гармоническое колебание:

.

Кинетическая энергия системы, совершающей гармоническое колебание:

.

Полная механическая энергия системы, совершающей гармоническое колебание:

.

Работа –это процесс превращения одних форм движения материи в другие и одновременно количественная характеристика этого процесса.

Механическая работа – процесс, в котором под действием сил изменяется энергия системы, и одновременно количественная мера этого изменения.

Элементарная работа некоторой силы F, действующей на материальную точку (тело, систему), вызывающей элементарное перемещение dr (рис. П1.29):

dA = Fdr = Fdrcos = F_rdr.

Работа нескольких сил, действующих на тело (материальную точку, систему), – алгебраическая сумма работ, совершаемых отдельно взятой силой на данном перемещении:

.

Работа по перемещению массы в поле сил тяготения

.

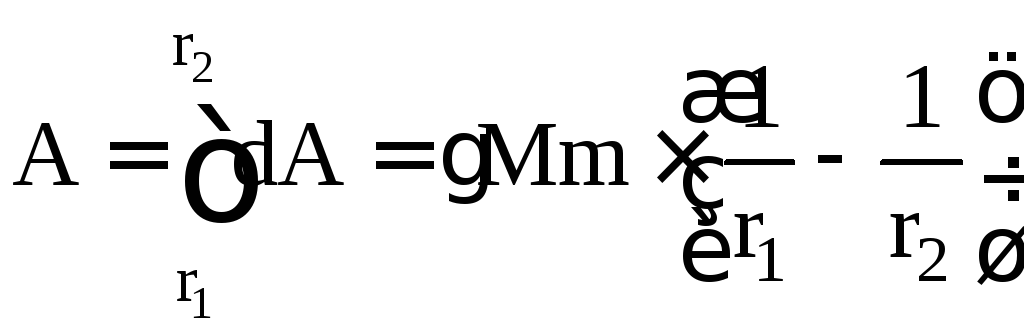Работа консервативных (потенциальных) сил по замкнутой траектории равна нулю:

.

Работа, совершаемая при движении материальной точки (тела, системы) по криволинейной траектории:

.

Работа, совершаемая внешними силами при вращательном движении относительно неподвижной оси за время dt:

,

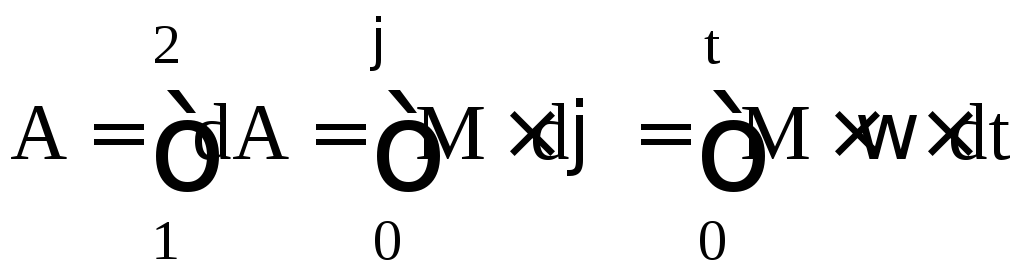где M – результирующий момент всех внешних сил;

ω – угловая скорость.

Работа постоянной проекции результирующего момента M на выбранное направление:

,

где M = I = I(d/dt);  = dt.

Работа возвращающей силы при изменении положения колеблющейся системы на dx:

dA = Fdx = –kxdx.

Работа возвращающей силы при изменении положения колеблющейся системы на x:

,

где x = x₀ sin(ω₀t + φ₀) – смещение системы от положения равновесия.

Мощность – физическая величина, численно равная работе, совершаемой в единицу времени. Мощность характеризует работоспособность машин и механизмов.

Средняя мощность – физическая величина, численно равная отношению работы, совершенной за некоторый промежуток времени t, к величине этого промежутка времени:

.

Мгновенная мощность определяется как первая производная от работы по времени:

N = dA/dt = d (F_sdS)/dt = Fv,

где F – мгновенная сила;

v – мгновенная скорость.

Максимальная мощность при равноускоренном движении (F = = const):

N_max = Fv_max; <N> = F<v>.

Мгновенная мощность при вращательном движении

,

где M – мгновенный момент силы;

ω – мгновенная угловая скорость.

Закон сохранения энергии в его общефизическом смысле – энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой, в количественном отношении оставаясь неизменной.

Закон сохранения и превращения механической энергии: полная механическая энергия замкнутой системы (при отсутствии внешних воздействий), в которой действуют только консервативные силы, остается величиной постоянной:

W_k + W_p = const.

Закон сохранения импульса: полный импульс замкнутой системы при отсутствии внешних воздействий остается величиной постоянной (рис. П1.30):

p = const.

Закон движения центра масс: центр масс системы движется как материальная точка, в которой сосредоточена масса всей системы и на которую действует равнодействующая всех внешних сил:

.

Импульс незамкнутой системы сохраняется, если геометрическая сумма всех внешних сил равна нулю.

Удар – совокупность явлений, возникающих при столкновении движущихся твердых тел, а также при некоторых видах взаимодействия твердого тела с жидкостью или газом.

Ударный импульс – мера механического взаимодействия тел при ударе ударной силы F за время удара τ:

.

Коэффициент восстановления k – величина, характеризующая потери энергии при ударе, численно равная отношению скорости взаимодействующих масс после взаимодействия к их скорости до взаимодействия:

.

Центральный удар – такой удар, при котором центры масс тел лежат на линии удара.

Прямой центральный удар – такой, при котором скорости v₁ и v₂ центров масс в начале удара направлены параллельно линии удара.

Центральный абсолютно неупругий удар шаров характеризуется тем, что выполняется только закон сохранения импульса. Скорость шаров после центрального абсолютно неупругого удара

.

Центральный абсолютно упругий удар шаров характеризуется тем, что выполняются законы сохранения полной механической энергии и импульса. Скорости шаров после взаимодействия:

;.

Закон сохранения момента импульса – момент импульса замкнутой системы в отсутствие внешних воздействий остается величиной постоянной:

, а L₀ = const.

Скорость изменения момента импульса (уравнение моментов):

,

где L₀ – момент импульса тела (системы) относительно начала координат;

M_вн – суммарный вращающий момент внешних сил, действующих на тело.