методичка_математика_661

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежская государственная лесотехническая академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

– нулевая матрица.

– нулевая матрица.

.pdf

Скачиваний:

Добавлен:

11.04.2015

Размер:

584 Кб

Скачать

☆

1 / 71 2 3 4 5 6 7 > Следующая >>>

Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования «Воронежская государственная лесотехническая академия»

МАТЕМАТИКА

ЛИНЕЙНАЯ АЛГЕБРА

Методические указания и индивидуальные задания для студентов 1 курса специальностей

190601 – Автомобили и автомобильное хозяйство,

190702 – Организация и безопасность движения,

190603 – Сервис транспортных и технологических машин и оборудования (автомобильный транспорт)

Воронеж 2010

УДК 512

Сапронов, И. В. Математика. Линейная алгебра [Текст] : метод. указания и индивидуальные задания для студентов 1 курса специальностей 190601 – Автомобили и автомобильное хозяйство, 190702 – Организация и безопасность движения, 190603 – Сервис транспортных и технологических машин и оборудования (автомобильный транспорт) / И. В. Сапронов, В. В. Зенина, А. В. Макарова ; Фед. агентство по образованию, ГОУ ВПО «ВГЛТА». –

Воронеж, 2010. – 64 с.

Печатается по решению учебно-методического совета ГОУ ВПО «ВГЛТА» (протокол № 8 от 11 июня 2009 г.)

Рецензент д-р физ.-мат. наук, проф. кафедры алгебры и топологических методов анализа ВГУ Ю.Е. Гликлих

ОГЛАВЛЕНИЕ

I. Матрицы и определители . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4 1. Линейные операции над матрицами . . . . . . . . . . . . . . . . . . . . . . . 5 2. Перемножение матриц . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6 3. Определители . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 4. Обратная матрица . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17 5. Ранг матрицы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20

II. Системы линейных алгебраических уравнений . . . . . . . . . . . . . 23 1. Метод Гаусса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24 2. Правило Крамера . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27 3. Решение систем линейных алгебраических уравнений с

помощью обратной матрицы . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28 4. Общее решение однородной системы линейных алгебраических уравнений . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29

5. Структура общего решения неоднородной системы линейных алгебраических уравнений . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32

6. Собственные векторы и собственные значения матрицы . . . . . 36 III. Варианты индивидуальных заданий . . . . . . . . . . . . . . . . . . . . . . 39

Библиографический список . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 64

Методические указания содержат необходимый теоретический материал и решения практических примеров, которые помогут студентам выполнить индивидуальные задания по разделам: матрицы и определители, системы линейных алгебраических уравнений.

Материалы данной методической разработки по содержанию, форме изложения и объему соответствуют задачам дисциплины и требованиям стандарта соответствующей специальности.

I. Матрицы и определители

Определение. Матрицей порядка m ×n называется прямоугольная таблица чисел вида

a	a	...	a
11	12		1n
a21	a22	...	a2n
A =	...	...	...	.
...	...	...	...
	am2	...
am1	am2	...	amn

Обозначения: A – матрица, aij – элемент матрицы, i – номер строки, в которой стоит данный элемент, j – номер соответствующего столбца; m – число строк матрицы, n – число ее столбцов.

Определение. Матрица называется квадратной, если m = n . Число n в этом случае называют порядком квадратной матрицы.

Определение. Матрицы одинаковой размерности называются равными, если у них соответственно равны элементы, стоящие на одинаковых местах.

Пример 1. Если матрица		−1	3		−1	3	, то A = B .
Пример 1. Если матрица	A =			и матрица B =			, то A = B .
		5	4		5	4
		5	4		5	4

Определение. Матрица называется нулевой, если все ее элементы равны

Определение. Элементы aii в матрице A называются диагональными и

образуют главную диагональ.

Определение. Квадратная матрица называется единичной (обозначается E ), если элементы, стоящие на ее главной диагонали, равны 1, а остальные равны 0.

1. Линейные операции над матрицами

Определение. Произведением матрицы на число называется матрица той же размерности, что и исходная, все элементы которой равны элементам исходной матрицы, умноженным на данное число.

определения получаем	3 3	3 5 3	7		9 15 21
определения получаем	3 A =			=			.
		(−1) 3
	3 2 3	(−1) 3	0		6 −3 0
Определение. Суммой матриц A и B одинаковой размерности m ×n
называется матрица C той же размерности, каждый элемент которой
равен сумме элементов матриц A и B , стоящих на тех же местах:
cij = aij +bij , i =1,..., m , j =1,..., n .
	2 −3 1 1						−1 4 0 −1
Пример 5. Найти сумму матриц A =						и B =		.
			−2 8				2 −2 5 7
	0 4		−2 8				2 −2 5 7

Решение.

Вычислим элементы матрицы C = A + B , складывая элементы исходных матриц, стоящие на одинаковых местах:

2 +(−1) −3 + 4				1 +0 1 +(−1)				1	1	1	0
C = A + B =							=					.
	0	+ 2 4 +(−2)		−2 +	5 8 +7			2	2	3	15
	0	+ 2 4 +(−2)		−2 +	5 8 +7			2	2	3	15
Пример 6. Найти матрицу 5A −2B , если
		2 −3 1	,		4 3	2
A =			,	B =			.
					−3 1
		−1 0 −2			−3 1	−4

Решение.

5 2		5 (−3)	5 1			=	10	−15				5		,
5A =						=								,
	(−1)	5 0						0			−10
5	(−1)	5 0	5 (−2)				−5	0			−10
2 4		2 3	2 2		8 6 4					,
2B =					=					,
	(−3) 2 1 2 (−4)							−8
2	(−3) 2 1 2 (−4)				−6 2			−8
	10 −8		−15 −6				5 −4		=		2		−		21 1
5A −2B =									=							.
		−(−6)										1		−2 −2
	−5	−(−6)	0 −2 −10 −(−8)									1		−2 −2
		2	−21		1
Итак, 5A −2B =						.
			−2	−2
		1	−2	−2

2. Перемножение матриц
Определение. Произведением матрицы A размерности							m × p	и
матрицы B размерности p ×n называется матрица C				размерности m ×n ,
каждый элемент которой cij	определяется формулой: cij = ∑p				aikbkj ,		i =1,..., m ,
				k =1
j =1,...,n . Таким образом,	элемент	cij	представляет собой				сумму
произведений элементов i –й cтроки		матрицы A на		соответствующие
элементы j –го столбца матрицы B .
Операция перемножения матриц некоммутативна, т.е.				AB ≠ BA . Действи-
тельно, если существует произведение			AB , то BA	может		вообще		не
существовать из-за несовпадения размерностей. Если существуют и								AB ,
и BA , то они могут иметь разные размерности (если m ≠ n ).
Для квадратных матриц	одного	порядка произведения				AB и		BA

существуют и имеют одинаковую размерность, но их соответствующие элементы в общем случае не равны.

Пример 7. Выяснить, можно ли умножить друг на друга матрицы

0	3		5		6
	−2	и	5		6
A = 4	−2	и	B =			.
				7	8
1	−1			7	8
1	−1

Если произведение существует, вычислить его.

Решение.

Сравним размерности матриц A и B : A [3×2], B [2×2]. Следовательно,

n = l,

m ≠ k , поэтому произведение AB [3×2] существует, а произведение

BA – нет.

Найдем элементы AB :

0 5 +3 7

0 6 +3 8

0 + 21 0 + 24 21 24

4 5 +(−2) 7 4 6 +(−2) 8

−14 24 −16

AB =

1 5 +(−1) 7 1 6 +(−1)

−7

6 −8

−2

Таким образом,

, BA

не существует.

AB =

−2

Пример 8. Найти AB и BA , если

2 −2 1 0

, B =

−1 0

A =

−1 1

1 1

−3 1

Решение.

Проверим возможность перемножения матриц, определив их размерность.

A [2×4], B [4×2]. Следовательно, n = l = 4, m = k = 2, поэтому матрицы AB и BA существуют, причем AB [2×2], BA [4×4].

Для вычисления элементов матрицы C = AB элементы строк матрицы A умножаются на соответствующие элементы столбцов матрицы B :

3 +(−2) (−1) +1

1 +0 2

+(−2) 0

+1 1 +0

C = AB =

+1 (−1) +(−1)

1 +1 2 −

3 2 +1 0 +(−1) 1 +1 4

−3

6 + 2

+1 +0

4 +0 +1 +0

−6 +0 −1 + 4

−9 −1 −1 + 2

−9

−3

При вычислении элементов матрицы D = BA элементы строк матрицы B умножаются на элементы столбцов матрицы A :

3 2 + 2 (−3)

3 (−2) + 2 1

3 1 + 2 (−1)

3 0 + 2 1

D = BA =

−1 2 +0 (−3) −1 (−2) +0 1 −1 1 +0 (−1) −1 0 +0 1

1 2 +1 (−3)

1 (−2) +1 1

1 1 +1 (−1)

1 0 +1 1

2 2 + 4 (−3)

2 (−2) + 4 1

2 1 + 4 (−1)

2 0 + 4 1

6 −6

−6 + 2 3 −2 0 + 2

−4 1 2

−2 +0 2 +0 −1 +0 0 +0

−2 2 −1 0

2 −3

−2 +1 1 −

1 0 +1

−1

−1 0 1

4 −12

−4 + 4 2 −

4 0 + 4

−8 0 −2 4

Задачи для самостоятельного решения

а) Найти произведение матриц				AB , где
		1		2	0	−1			5			1
		1		2	0	−1				−1		0
								, B		−1		0
	A =		0 4 0 −1					, B	=	1		1		.
			−2 1		0	3				1		1
			−2 1		0	3				0		−2
										0		−2
б) Найти произведения	AB		и	BA , где
										2
											7
											7
		A = (4 −1 0 2), B =										.
											1
											0
											0
в) Найти значение выражения				3A −	1 BC ,		где
					2
	3	−4			2		0	1				7		−7
	1 0					0 3 2						7		−7
A =	1 0					0 3 2							2 0
A =	0 −1			, B =					, C			=	2 0		.
	0 −1					−1 0 −3							0	−3
	2	3				5	2	0					0	−3
	2	3				5	2	0

3. Определители

Определение. Определителем второго порядка называется число,

полученное с помощью элементов квадратной матрицы 2–го порядка следующим образом:

=	a11	a12	= a11a22 −a21a12 .
	a21	a22

При этом из произведения элементов, стоящих на так называемой главной диагонали матрицы (идущей из левого верхнего в правый нижний угол) вычитается произведение элементов, находящихся на второй, или побочной, диагонали.

Пример 8.	1	−3	=1 8 −5 (−3) =8 +15 = 23
Пример 8.	1	−3	=1 8 −5 (−3) =8 +15 = 23
	5	8

Определение. Определителем третьего порядка называется число,

определяемое с помощью элементов квадратной матрицы 3–го порядка следующим образом:

a11 a12 a13

= a21 a22 a23 = a11a22a33 + a12a23a31 + a21a32a13 −a31a22a13 −a21a12a33 −a32a23a11 . a31 a32 a33

Для того чтобы легче запомнить эту формулу, можно использовать следующие правила:

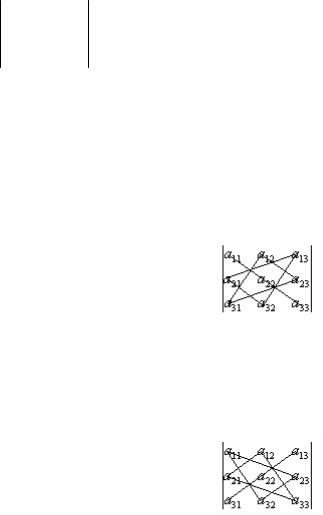
1) Правило треугольников.

Оно заключается в следующем: элементы, произведения которых входят в определитель со знаком «+», располагаются так:

образуя два треугольника, симметричных относительно главной диагонали. Элементы, произведения которых входят в определитель со знаком «–», располагаются аналогичным образом относительно побочной диагонали:

Пример 9. Вычислить определитель

Решение.

Вычислим определитель 3–го порядка, используя его определение:

= 0 + 24 +5 −0 −3 +8 = 34

2) Правило Саррюса.

К определителю справа приписывается первый и второй столбцы и элементы, стоящие на диагоналях полученной таблицы, перемножаются, а затем эти произведения складываются, причем произведения элементов на диагоналях, идущих снизу вверх, берутся со знаком минус:

	a11	a12	a13	a11	a12
	a11	a12	a13	a11	a12
=	a21	a22	a23	a21	a22	= a11a22a33 + a12a23a31 + a13a21a32 −a31a22a13 −a32a23a11 −a33a21a12
	a31	a32	a33	a31	a32

Пример 10.

3	2	1	3	2
3	2	1	3	2
4	3	2	4	3 = 3 3 3 + 2 2 5 +1 4 4 −5 3 1 −4 2 3 −3 4 2 =
5	4	3	5	4

= 27 + 20 +16 −15 −24 −24 = 0

Пример 11.

3 1 1 3 1 4 1 1 4 1 = 3 1 1 +1 1 5 +1 4 2 −5 1 1 −2 1 3 −1 4 1 = 3 +5 +8 −5 −6 −4 =1 5 2 1 5 2

Задачи для самостоятельного решения

Вычислить определители второго и третьего порядка:

а)	2	1	;	б)	1	−1	;	в)	1	2	;
а)	2	1	;	б)	1	−1	;	в)	1	2	;
	3	−1			2	3			0	4

1 / 71 2 3 4 5 6 7 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.03.2016978 Кб75методичка 130.pdf
#
11.04.2015706 Кб34методичка к курсовой экономика.doc
#
11.04.2015757 Кб26Методичка ФМ практика ПМ очное.doc
#
11.04.2015562 Кб33Методичка ФМкурсяк ПМ очное.doc
#
11.04.20153 Мб117Методичка_ AutoCAD.pdf
#
11.04.2015584 Кб25методичка_математика_661.pdf
#
15.03.2016161 Кб44Методы исследования.docx
#
11.04.20151 Мб95Метрология.docx
#
11.04.201544 Кб22Министерство образования и науки РФ.docx
#
15.03.2016131 Кб64мировая автомобилизация.doc
#
11.04.2015176 Кб26мировые рынки.docx

a	a	...	a
11	12		1n
a21	a22	...	a2n
A =	...	...	...	.
...	...	...	...
	am2	...
am1	am2	...	amn

a	a	...	a
11	12		1n
a21	a22	...	a2n
A =	...	...	...	.
...	...	...	...
	am2	...
am1	am2	...	amn

a	a	...	a
11	12		1n
a21	a22	...	a2n
A =	...	...	...	.
...	...	...	...
	am2	...
am1	am2	...	amn