2. Парная регрессия и корреляция

1. Виды взаимосвязей. Уравнение парной регрессии

С помощью регрессионного анализа строится и проверяется модель стохастической связи между одной зависимой (т.е. эндогенной) и одной и более независимыми (т.е. экзогенными) и предопределенными переменными.

Мы уже отмечали, что различают два вида взаимозависимостей между экономическими явлениями и процессами: а) функциональная (детерминированная), б) стохастическая (не детерминированная). Например, доход агента по продажам может быть определен как фиксированный оклад “” плюс премия “” от объема продаж. Как только мы узнаем объем продаж, то сможем определить Y как . Для построения такой модели нет необходимости в регрессионном анализе. Если мы знаем два значения Х – объемы продаж и соответствующие им Y, то, проведя на графике прямую через эти две точки, мы получим графическое отображение модели зависимости дохода агента от величины его заработной платы и объема произведенных продаж.

Y

y₂

y₁

x₁ x₂ X

Рис. 1 Детерминированный характер зависимости между X и Y

Регрессия - это односторонняя стохастическая зависимость. Например, при изучении потребления энергии в зависимости от объема производства речь идет об односторонней связи и, следовательно, о регрессии. Как правило, при построении регрессионной модели мы исходим из того, что - случайная величина, а Х - неслучайная переменная с фиксированными значениями.

При известной величине мы имеем распределение множества значений Y, то есть модель имеет вероятностный характер может быть записана для двух линейно зависимых переменных в общем виде так:

(2.1),

где постоянная величина (свободный член уравнения). При Х = 0, . Интерпретируется в зависимости от экономического смысла задачи. Чаще всего отражает совокупное воздействие на Y неучтенных X-ом факторов.

коэффициент регрессии, отражает наклон линии, вдоль которой рассеяны данные наблюдений. Модель интерпретируется как показатель изменения Y при изменении X на единицу измерения признака. Знак плюс при указывает на положительный характер связи между Y и X и наоборот.

- ошибка, называемая, так же, остатком. Она отражает тот факт, что изменения Y лишь приблизительно описываются изменениями X, то есть процесс носит стохастический характер и существуют другие факторы не учтенные в данной модели.

Функция регрессии в отличие от строгой математической функции не является обратимой. Поясним, что мы имеем в виду. Так функция х = 0,5y является обратной по отношению к функции у = 2х. Задаваясь значением х = 3, получим у = 6. Задаваясь для обратной функции значением y = 6, получим х = 3.

Необратимость функции регрессии обусловлена. Во-первых, самой структурой явления, определяющей направление связи; во-вторых, постановкой задачи исследования, когда преследуется вполне определенная цель: как по значениям одной переменной, выбранной в качестве аргумента, предсказать соответствующие значения другой (функции): в третьих, способом измерения отклонения эмпирических точек. Вследствие этого, если исследуют стохастическую зависимость переменной Y от X, то определяют регрессию Y на X.

Регрессия может быть различного вида.

1. Относительно числа явлений (переменных), учитываемых в регрессии, различают:

а) простую регрессию межу двумя переменными. Например, прибыль предприятия (зависимая переменная) от производительности труда (объясняющая переменная);

б) множественную регрессию между зависимой переменной y и несколькими причинно обусловленными объясняющими (независимыми, или предсказывающими) переменными х₁,х₂,...,х_n. Например, зависимость заработной платы работника от его возраста, образования, квалификации, стажа, отрасли и др.

2. Относительно формы зависимости различают:

а) линейную регрессию;

б) нелинейную регрессию.

2. Оценка параметров модели парной регрессии. Расчет коэффициентов регрессии.

Метод регрессионного анализа рассмотрим на следующем примере. Предположим, некоторая фирма торгует фасованными молочными продуктами и её интересуют ежедневные объемы продаж в магазинах города, например, литровых пакетов с молоком. Для выявления возможной взаимосвязи между числом покупателей в магазине и объемом реализации проведено обследование в 20 случайно выбранных магазинах города:

Таблица 2.1. Число покупателей и дневной объем продаж пакетного молока 20 магазинах города

Номер магазина	Число посетителей	Выручка (усл ден. ед.)
1	907	1120
2	926	1105
3	506	684
4	741	921
5	789	942
6	889	1008
7	874	945
8	510	673
9	529	724
10	420	612
11	679	763
12	872	943
13	924	946
14	607	764
15	452	692
16	729	895
17	794	933
18	844	1023
19	1010	1177
20	621	741

Данные, приведенные таблице, можно представить в более наглядном виде на точечной диаграмме (рис.2). Диаграмма наглядно показывает наличие положительной линейной взаимосвязи между числом посетителей магазина и выручкой от продажи молока, то есть можно предположить, что для приведенных данных будет адекватна модель вида (2.1): где Х – число посетителей магазина, а Y – выручка от продажи.

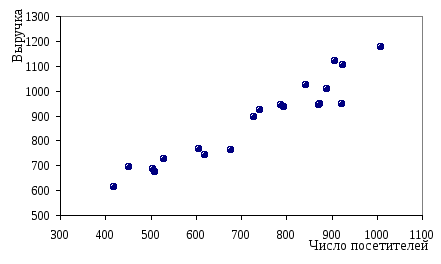
Рис.2. Точечная диаграмма рассеяния данных о сумме выручки от продажи молока в различных магазинах города

Обращаясь к диаграмме, отметим, что через точки на графике можно провести несколько линий, удовлетворяющих выражению (2.1), а нам необходимо выбрать лишь одну, наилучшую.

При построении регрессионной модели мы, как правило, располагаем лишь выборочными данными, поэтому, полученные при подстановке данных коэффициенты регрессии будут лишь оценками истинных значений генеральных параметров модели.

Уравнение регрессии, полученное по выборочным данным, можно записать так

(2.2),

где - оценки истинных коэффициентов регрессии.

Следовательно, для каждого значения данных существует фактическое (наблюдаемое) значение , но при использовании выражения (2.2) появляется так же оценочное значение . Разность -. это оценка ошибки, Чтобы не путать cо случайной ошибкой в модели истинной регрессии , обозначим её и назовем остатком.

При статистической проверке взаимосвязи между X и Y необходимо найти такие оценки значений в выражении (2.1), чтобы они были наилучшими, линейными и несмещенными (BLUE – Best, Linear, Unbiased Estimator).

Понятие наилучшие относится к требованию эффективности оценок параметров, то есть дисперсия оценок параметров должна быть наименьшей из всех возможных.

Термин линейность просто повторяет, что взаимосвязь линейна.

Несмещенность означает, что ожидаемые значения коэффициентов регрессии должны являться истинными коэффициентами.

Н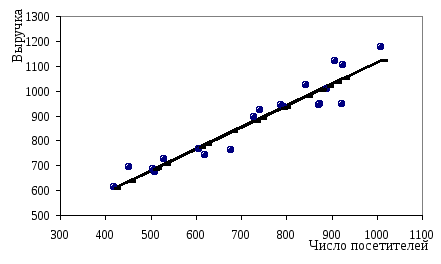аиболее часто для нахождения параметров уравнения регрессии используется МНК, который дает наилучшие несмещенные оценки. Найденная с помощью МНКлиния регрессии минимизирует сумму квадратов отклонений , то есть . Это показано на рис. 3

Рис. 3

Проверка того удовлетворяют ли полученные с помощью МНК оценки параметров вышеуказанным условиям, проводится путем анализа остатков. Мы уже указывали, что в уравнении регрессии Y – случайная величина, следовательно, линейно связанная с ней ошибка - случайная величина, которая должна удовлетворять следующим условиям.

1. Нормальности

2. Гомоскедастичности

3. Независимости ошибок

(Этим же условиям должны удовлетворять Y-ки, однако анализ остатков модели более удобен).

Первое предположение – нормальности - требует, чтобы остатки были нормально распределены.

Второе условие – гомоскедастичности - требует, чтобы вариация вокруг линии регрессии была постоянной для всех значений . Это означает, что вариация , а, следовательно, и имеет одни и те же значения и в случаях, когда имеет наибольшие значения, и в случаях, когда мало. Если оно нарушается, то мы говорим о гетероскедастичности модели. Это условие очень важно для использования МНК для определения коэффициентов регрессии.

Третье условие независимости ошибок требует, чтобы ошибки (“остатки” - разность между теоретическими и эмпирическими значениями) были независимы для каждого значения Х. Это условие часто относится к данным, которые собираются за некоторый период времени. Например, данные, собранные за какой-нибудь период, могут коррелировать с данными за предыдущий период, в этом случае мы говорим, что данные автокоррелированы.

Так как Y – случайная величина, в случае линейной зависимости для любых значений X значения Y будут нормально распределены и таким образом, статистическое распределение может быть полностью описано при помощи средней и дисперсии:

(2.3).

Так как и - постоянны, а - нестохастична, это выражение преобразуется в

(2.4).

Однако поскольку математическое ожидание равно нулю, то выражение (4) превращается в

(2.5).

Так как математическое ожидание равно нулю, то дисперсия , которая служит так же дисперсией равна

(2.6),

то есть дисперсия равна среднему значению квадратов остатков модели.

Отсюда нормально распределено с параметрами . Это показано на рисунке 4.

Рис. 4

Для предсказания значений Y нам необходимо определить два коэффициента - свободный член уравнения и - наклон линии регрессии. После того как они будут определены, линия регрессии может быть перенесена на график. Мы сможем визуально оценить насколько хорошо наша статистическая модель подогнана к реальным данным. Мы можем увидеть близки ли выборочные данные к линии регрессии или значительно отклоняются от нее.

В настоящее время решение регрессионных уравнений, как правило, проводится с помощью специализированных компьютерных программ.

Величины, минимизирующие суммы квадратов отклонений от для случая парной регрессии, находятся следующим образом:

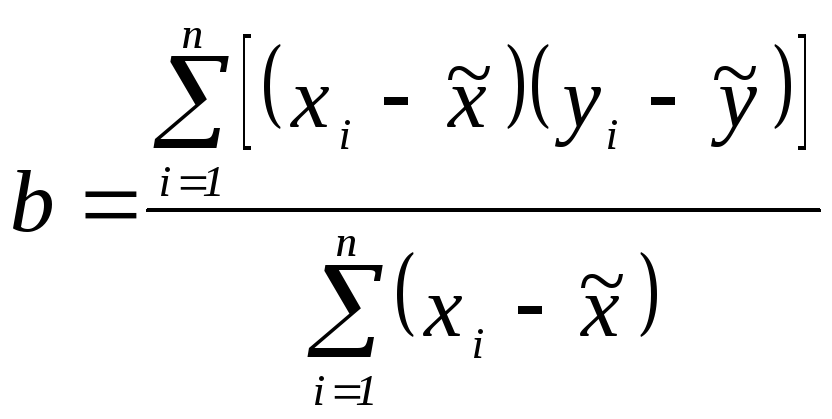(2.7)

(2.8)

Значения ошибок, называемые обычно остатками, рассчитываются как

(2.9)

Используя данные примера, получим следующее уравнение для “лучшей” линии регрессии:

.

Наклон линии регрессии . Это означает, что при увеличении Х на единицу ожидаемое значение Y возрастет на 0,873 единицы. То есть регрессионная модель предсказывает, что каждый новый посетитель магазина в среднем увеличивает ежедневную сумму реализации молока на 0,873 условных денежных единиц (или мы можем сказать, что мы можем ожидать прирост ежедневной реализации на 87,3 денежных единицы, если привлечем в магазин добавочно 100 посетителей). Отсюда, наклон может быть рассмотрен как прирост дневных продаж, который оценивается варьирующими относительно числа посетителей магазина.

Свободный член уравнения получился равным +243,2 условных денежных единицы. Свободный член представляет значение Y при Х равном нулю. Поскольку мало вероятно число посетителей магазина равное нулю, то мы можем интерпретировать Y как прирост дневной выручки, который варьирует с другими факторами (не с числом посетителей).

Регрессионная модель может быть использована для прогнозирования суммы ежедневной реализации молока. Например, нас интересует прогноз реализации молока в магазинах, которые посещают по 600 покупателей в день. Подставим x_i = 600 в наше регрессионное уравнение:

.

Отсюда прогнозируемая дневная выручка для магазина с 600 посетителей равна 766,1 условных денежных единиц.

При прогнозировании значений зависимой переменной по уравнению регрессии, важно помнить, что нам доступны только те значения независимых переменных, которые находятся в интервале от наименьших до наибольших значений, использованных при создании модели. Отсюда, когда мы предсказываем Y по заданным значениям Х, мы можем интерполировать значения в пределах заданных рангов, но мы не можем экстраполировать вне рангов значений Х. Например, когда мы используем число посетителей для предсказания дневной выручки магазина, то мы знаем из данных примера, что их число находится в пределах от 420 до 1010. Следовательно, предсказание дневной выручки может быть сделано только для магазинов с числом покупателей в пределах от 420 до 1010 человек.

2. Стандартная ошибка оценки уравнения регрессии

Хотя метод наименьших квадратов дает нам линию регрессии, которая обеспечивает минимум вариации, не все наблюдения совпадают с линией регрессии. Поэтому необходима статистическая мера вариации фактических значений Y от предсказанных значений Y. Мера вариации относительно линии регрессии называется стандартной ошибкой оценки.

Стандартная ошибка оценки определяется как

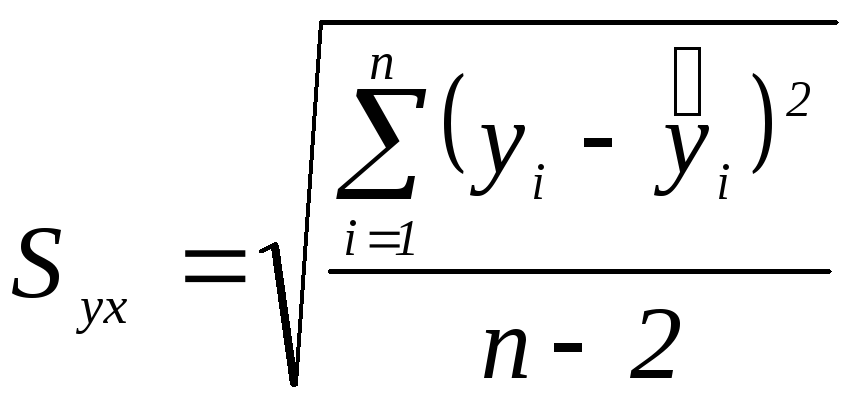(2.10),

где

- фактические значения зависимой переменной для заданных значений независимой переменной .

- предсказанные значения зависимой переменной для заданных значений независимой переменной .

Для нашего примера: и характеризует меру вариации фактических данных вокруг линии регрессии. Интерпретация этой меры аналогична среднему квадратическому отклонению. Стандартная ошибка оценки может быть использована для выводов о значении и определения является ли статистически значимым взаимоотношение между двумя переменными.

2. Измерение вариации в уравнении регрессии

Для проверки того, как хорошо независимая переменная предсказывает зависимую переменную в модели, необходим ряд мер вариации. Первая мера - общая сумма квадратов (S_T) - есть мера вариации значений относительно их среднего

(2.11).

В регрессионном анализе общая сумма квадратов может быть разложена на объясняемую вариацию (или сумму квадратов объясняемую регрессией) (S_R) и необъясняемую вариацию или остаточную сумму квадратов (S_E). Эти различные меры вариации отображены на рисунке:

y

Линия регрессии

_i

S_E

S_T

S_R

y₌

X

x_i

Рис.5

Сумма квадратов, объясняемая регрессией, (S_R), основывается на разнице между средним значением зависимой переменной и значением этой же переменной, предсказанным по регрессионному уравнению:

(2.12).

Остаточная сумма квадратов (S_E) представляет часть вариации y, которая не объясняется регрессией. Она основывается на разнице между значениями и

(2.13).

Эти меры вариации могут быть представлены следующим образом:

S_T = S_R + S_E (2.14).

Из формулы (2.13) видно, что - это выражение, стоящее под знаком корня в формулe (2.10) стандартной ошибки оценки. Компьютерные программы обычно вначале вычисляют значение сумму квадратов ошибки. В распечатке регрессионного уравнения, полученного на компьютере, 468336,40896, общая сумма квадратов = 513604,95000, а объясняемая вариация или сумма квадратов, объясняемая регрессией, = 468335,40896. Мы знаем, что S_T = S_R + S_E = 468335,40896 + 45269,54104 = 513604,95000

Отношение суммы квадратов отклонений, объясняемой регрессией, к общей сумме квадратов отклонений дает пропорцию изменения Y , объясняемого изменением X, и называется коэффициентом детерминации .

(2.15).

Отсюда коэффициент детерминации - мера пропорции вариации, которая объясняется независимыми переменными в регрессионной модели.

Для нашего примера R² = 46,9145 /51,3605 = 0,9119

Следовательно, 91,19% вариации еженедельной выручки магазинов можно объяснить числом покупателей, варьирующим от магазина к магазину. Только 8,7% вариации можно объяснить иными факторами.

При построении уравнения регрессии для двух переменных мы объясняли взаимоотношения между ними как предсказание значений зависимой переменной Y по значениям независимой переменной X. С другой стороны мы знаем, что интенсивность взаимосвязи между двумя переменными измеряет коэффициент корреляции. Корреляционная связь может быть различного типа: положительная, отрицательная, либо отсутствовать. Сила корреляционной связи между двумя переменными в генеральной совокупности измеряется при помощи коэффициента корреляции, значения которого находятся в пределах от +1 для полной положительной корреляции до -1 при полной отрицательной корреляции.

Выборочный коэффициент корреляции можно определить как

(2.16).

В парной линейной регрессии R имеет тот же знак что и _. Если положительно, то и положительно, если отрицательно, то - отрицательно, если рано нулю, то и равно нулю.

В нашем примере = 0,913 и - положительно, коэффициент корреляции R = 0,956. Близость коэффициента корреляции единице свидетельствует о сильной взаимосвязи между выручкой магазина и числом посетителей.

Хотя мы интерпретировали коэффициент корреляции в терминах регрессии, однако, как отмечалось выше, корреляция и регрессия - две различные техники. Корреляция устанавливает силу связи между признаками, а регрессия - форму этой связи. В ряде случаев для анализа достаточно найти меру связи между признаками, без использования одного из них в качестве предиктора для другого.

5. Интервал для прогноза оценки 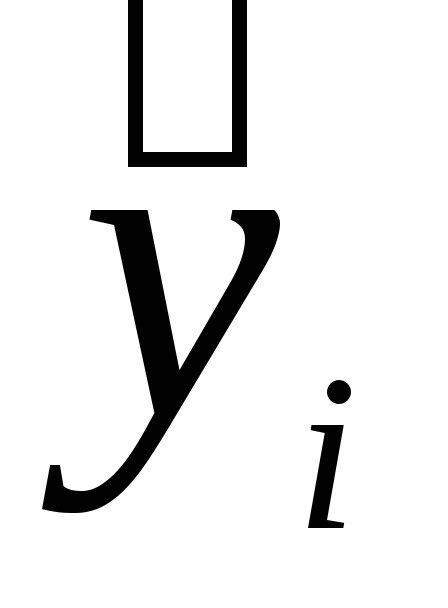и доверительный интервал генерального значения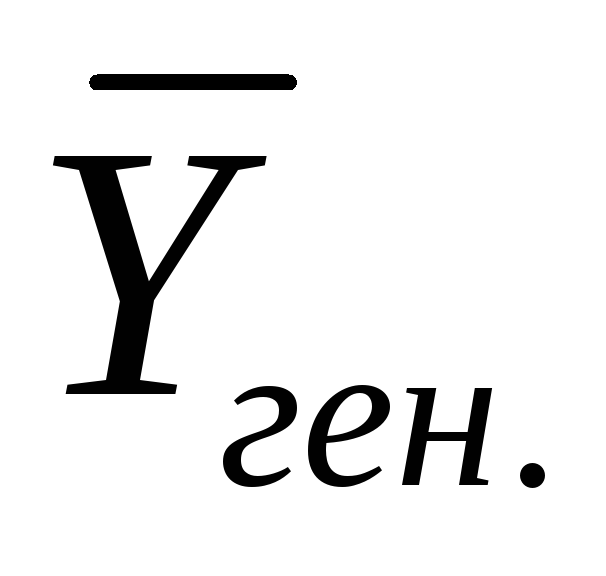

Поскольку в основном для построения регрессионных моделей используются данные выборок, то и интерпретация взаимоотношений между переменными в генеральной совокупности базируется на выборочных результатах.

Как мы уже говорили, регрессионное уравнение используется для прогноза значений Y по заданному значению X. В нашем примере мы уже показали, что, например, при 600 посетителях магазина сумма ожидаемая выручки 7661 усл. ден. ед. Однако это значение - только точечная оценка истинного среднего значения. Мы знаем, что для оценки истинного значения генерального параметра необходимо построение доверительного интервала. В случае с регрессионными параметрами, доверительный интервал для значений , лежащих на линии регрессии, имеет вид:

(2.17),

где

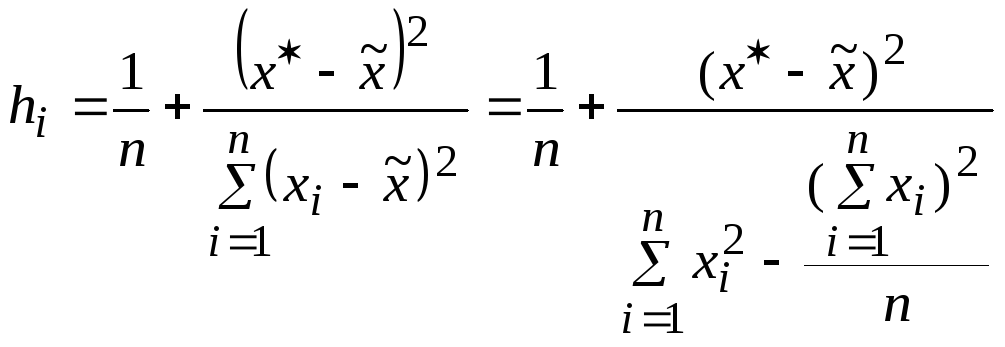(2.18),

- прогнозное значение зависимой переменной;

- стандартная ошибка оценки;

n - объем выборки;

- заданное значение .

Анализ выражения (2.18) указывает на то, что ширина интервала зависит от нескольких факторов. Для заданного уровня значимости увеличение вариации вокруг линии регрессии, как меры стандартной ошибки оценки, увеличивает ширину интервала. Однако, можно ожидать, что увеличение размера выборки сузит интервал. Более того, ширина интервала так же варьирует с различными значениями . Когда оценивается по значениям близким к , то интервал тем уже, чем меньше абсолютное отклонение от .

Когда оценка осуществляется по значениям , удаленным от среднего , то длина интервала возрастает. Этот эффект виден из выражения под квадратным корнем в (2.17) и рисунке 6.

Y

Х

Рис.6.

Определим интервал оценки суммы реализации от пакетного молока в магазине, который посетят 600 покупателей:

Следовательно, с 95% уверенностью можно утверждать, что ежедневная выручка отдельногомагазина, который посетили 600 покупателей, находится в пределах от 657,7 до 874,5 усл.ден.ед.

Если мы хотим сделать вывод относительно выручки во всех магазинах, которые в среднем посещает 600 покупателей, то необходимо построить доверительный интервал для генерального среднего значения при заданном X. Вариация в этом случае будет меньше, поскольку мы имеем дело не с отдельным, а со средним значением Y. Следовательно, интервал будет уже.

(2.19)

5. Интервал для оценки истинных значений параметра уравнения регрессии

Построим доверительный интервал для оценки истинных значений неизвестного параметра уравнения регрессии . Для этого проверим гипотезу о равенстве нулю . Сформулируем нулевую и альтернативную гипотезы:

Если гипотеза будет отклонена, то подтверждается существование линейной зависимости между переменными Y и X. Для проверки гипотезы используется t-критерий (случайная величина, имеющая распределение Стьюдента с n-2 степенями свободы:

, (2.20),

где

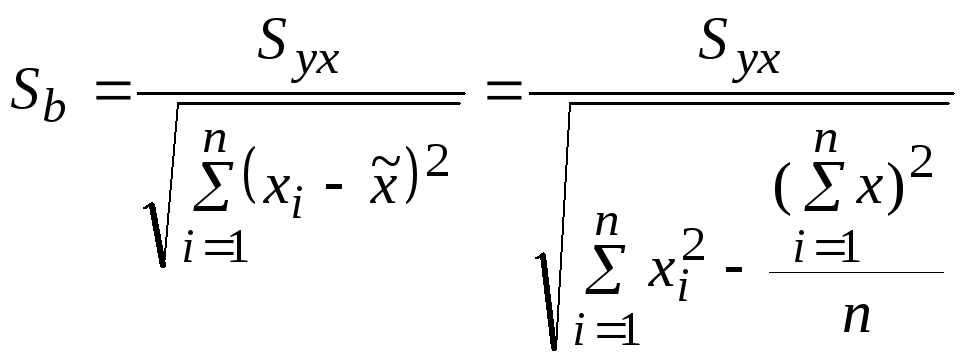(2.21).

Убедимся, что полученный выборочный результат является достаточным для заключения о том, что зависимость объема выручки от числа посетителей магазина существенна на 5% уровне значимости. Полученное значение 0,0639, при наблюдаемом значении t-критерия

.

По таблицам распределения Стьюдента найдем , Распечатка решения, полученная на компьютере, сразу указывает нам, что вероятность того, что значение коэффициента равно нулю, очень мала – 0,0001.

Таким образом, мы можем отклонить нуль-гипотезу об отсутствии линейной зависимости переменных в пользу альтернативной гипотезы и предположить с высокой вероятностью, что линейная зависимость между ежедневной выручкой от реализации молока и числом посетителей магазина существует.

5. F-критерий качества оценивания регрессии

Даже если между X и Y отсутствует зависимость, то по любой данной выборке может показаться, что такая зависимость существует. Для выяснения того, что полученное значение коэффициента детерминации не случайно используется F-критерий качества оценивания регрессии, который представляет собой отношение объясненной суммы квадратов S_R (в расчете на одну независимую переменную) к остаточной сумме квадратов S_E (в расчете на одну степень свободы):

(2.22)

где k – число независимых переменных.

F-критерий можно выразить через коэффициент детерминации:

(2.23)

F-критерий подчиняется распределению Фишера с двумя степенями свободы: - в числителе критерия проверки ( в нашем случае равна 1), - в знаменателе проверки (равна n-2).

Для нашего примера

Обратившись к таблицам распределения Фишера, мы видим, что табличное значение при 5% уровне значимости для = 1 и = 18 равно 4,41. То есть значение F-критерия свидетельствует о том, что полученное значение не случайно.