Указания к выполнению контрольных заданий

Задача 1 каждого варианта составлена по теме “Парная регрессия и корреляция”. Введем следующие обозначения:

- факторный признак, независимая (объясняющая) переменная,

- результативный признак, зависимая переменная,

x – фактические значения факторного признака,

y – фактические значения результативного признака,

- расчетные (полученные по уравнению регрессии) значения результативного признака,

a , b - параметры уравнения регрессии.

В контрольных заданиях используется уравнение парной линейной регрессии вида:

Рассмотрим методику выполнения на условиях конкретной задачи:

American Express Company в течение долгого времени полагала, что владельцы ее кредитных карт предпочитают оплачивать свои расходы во время путешествий при помощи их карт. Для выяснения этого из компьютерной базы компании были случайно выбраны 25 владельцев карточек, которым были заданы вопросы о числе миль, которые они провели в путешествиях. Данные опроса о расходах путешественников и числе миль, проведенных ими в пути, составляют исходную информацию задачи.

N п/п	Число миль, проведенных в пути, X	Расходы, у.е , Y	N п/п	Число миль, проведенных в пути, X	Расходы, у.е , Y
1	1211	1802	14	3209	4492
2	1345	2405	15	3466	4244
3	1422	2005	16	3643	5298
4	1687	2511	17	3852	4801
5	1847	2332	18	4033	5147
6	2026	2305	19	4267	5738
7	2133	3016	20	4498	6420
8	2253	3385	21	4533	6059
9	2400	3090	22	4804	6426
10	2468	3694	23	5090	6321
11	2699	3371	24	5233	7025
12	2806	3998	25	5439	6964
13	3082	3555

Пункт 1. Построение поля корреляции результата и фактора производится по исходным данным о парах значений факторного и результативного признаков с соблюдением масштаба. На основе поля корреляции делаются выводы о направлении и возможной функциональной форме связи между факторным и результативным признаками (прямая - обратная, линейная - нелинейная).

Для условий рассматриваемой задачи поле корреляции выглядит следующим образом:

Связь между факторным и результативным признаками прямая, линейная.

Пункт 2. Оценка параметров уравнения парной линейной регрессии производится обычным методом наименьших квадратов (МНК):, где

a и b –оценки параметров модели.

Величины, минимизирующие суммы квадратов отклонений отдля случая парной линейной регрессии, находятся как:

;

.

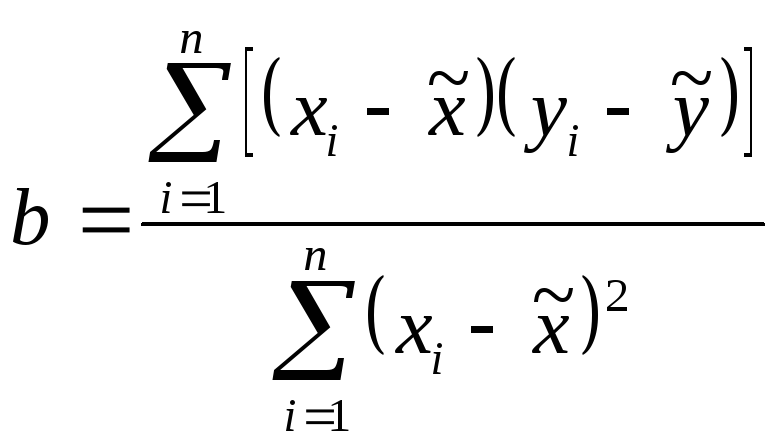Значения ошибок, называемые обычно остатками, рассчитываются как .

Проведите интерпретацию полученных результатов.

Расчет необходимых данных лучше всего организовать в таблице. Для нашего примера таблица будет выглядеть следующим образом:

Таблица 1

N/N	х	у
1	1211	1802	-1966,84	-2454,16	4826940	3868460	1787,652	14,34756
2	1345	2405	-1832,84	-1851,16	3392880	3359302	1955,831	449,1692
3	1422	2005	-1755,84	-2251,16	3952677	3082974	2052,471	-47,4707
4	1687	2511	-1490,84	-1745,16	2601754	2222604	2385,062	125,9377
5	1847	2332	-1330,84	-1924,16	2560749	1771135	2585,872	-253,872
6	2026	2305	-1151,84	-1951,16	2247424	1326735	2810,529	-505,529
7	2133	3016	-1044,84	-1240,16	1295769	1091691	2944,82	71,17973
8	2253	3385	-924,84	-871,16	805683,6	855329	3095,428	289,5722
9	2400	3090	-777,84	-1166,16	907085,9	605035,1	3279,922	-189,922
10	2468	3694	-709,84	-562,16	399043,7	503872,8	3365,266	328,7337
11	2699	3371	-478,84	-885,16	423850	229287,7	3655,186	-284,186
12	2806	3998	-371,84	-258,16	95994,21	138265	3789,477	208,5225
13	3082	3555	-95,84	-701,16	67199,17	9185,306	4135,875	-580,875
Продолжение таблицы 1
N/N	х	у
14	3209	4492	31,16	235,84	7348,774	970,9456	4295,268	196,7322
15	3466	4244	288,16	-12,16	-3504,03	83036,19	4617,819	-373,819
16	3643	5298	465,16	1041,84	484622,3	216373,8	4839,965	458,035
17	3852	4801	674,16	544,84	367309,3	454491,7	5102,273	-301,273
18	4033	5147	855,16	890,84	761810,7	731298,6	5329,439	-182,439
19	4267	5738	1089,16	1481,84	1613961	1186270	5623,124	114,8759
20	4498	6420	1320,16	2163,84	2856615	1742822	5913,044	506,9564
21	4533	6059	1355,16	1802,84	2443137	1836459	5956,971	102,0292
22	4804	6426	1626,16	2169,84	3528507	2644396	6297,093	128,9072
23	5090	6321	1912,16	2064,84	3948304	3656356	6656,041	-335,041
24	5233	7025	2055,16	2768,84	5690409	4223683	6835,515	189,4853
25	5439	6964	2261,16	2707,84	6122859	5112845	7094,058	-130,058
сумма	79446	106404			51398430	40952877	106404	0
Средн.	3177,84	4256,16

В соответствии с расчетами, представленными в таблице 1, а= 267,7715; b=1,2551

Соответственно уравнение регрессии может быть записано как:

Коэффициент регрессии линейной функции (b) есть абсолютный показатель силы связи, характеризующий среднее абсолютное изменение результата при изменении факторного признака на единицу своего измерения.

Полученное уравнение может быть объяснено следующим образом: с увеличением расстояния на 1 милю расходы путешественника в среднем увеличиваются на 1,2551 условных денежных единиц. Свободный член уравнения равен 267,7715, что может трактоваться как влияние на величину расходов других, неучтенных в модели факторов.

Пункт 3. Линейный коэффициент корреляции характеризует тесноту линейной связи между изучаемыми признаками. Его можно определить по следующей формуле:

.

Значения линейного коэффициента корреляции принадлежит промежутку [-1;1].

Чем ближе его абсолютное значение к 1, тем теснее связь между признаками. Положительная величина свидетельствует о прямой связи между изучаемыми признаками, отрицательная - о наличии обратной связи между признаками.

Для нашей задачи r=0,98329, что подтверждает вывод, сделанный в пункте 1, что связь между признаками прямая, а также указывает на очень сильную взаимосвязь между количеством миль, проведенных в пути и расходами.

Квадрат коэффициента (индекса) корреляции называется коэффициентом детерминации и показывает долю вариации результативного признака, объясненную вариацией факторного признака.

Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах. Например: =0,8 означает, что доля колеблемости результативного признака, объясненная вариацией фактора, включенного в уравнение регрессии, равна 80%. Остальные 20% приходятся на долю прочих факторов, не учтенных в уравнении регрессии.

Для нашей задачи коэффициент детерминации равен 0,9669, то есть 96,69% вариации результативного признака (расходов путешественников) объясняется вариацией факторного признака (количеством миль, проведенных в пути)

Пункт 4 связан с темой “Проверка статистических гипотез”. Рекомендуется использовать следующую общую процедуру проверки гипотез:

1. Сформулируйте нулевую гипотезу о том, что коэффициент регрессии статистически незначим: (линейной зависимости нет)

при конкурирующей: (линейная зависимость есть)

или о том, что уравнение в целом статистически незначимо: .

2. Определите фактическое значение соответствующего критерия.

3. Сравните полученное фактическое значение с табличным.

4. Если фактическое значение используемого критерия превышает табличное, нулевая гипотеза отклоняется, и с вероятностью (1-) принимается альтернативная гипотеза о статистической значимости коэффициента регрессии. Если фактическое значение t - критерия меньше табличного, оснований отклонять нулевую гипотезу - нет.

Статистическая значимость коэффициента регрессии проверяется с помощью t - критерия Стьюдента:

,

где

,

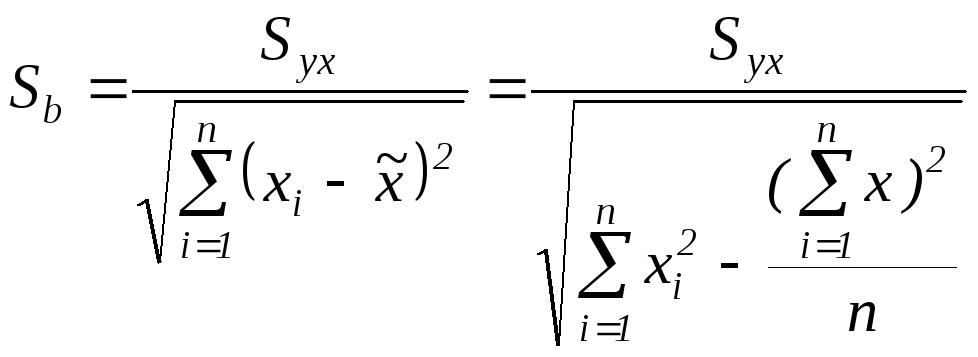- стандартная ошибка оценки, рассчитываемая по формуле

.

Так как нулевая гипотеза предполагает, что =0, то t_набл. рассчитывается как:

.

Для определения табличного значения воспользуйтесь таблицами распределения Стьюдента для заданного уровня значимости α, принимая во внимание, что число степеней свободы для распределения Стьюдента равно (k = n - 2).

Для нашего примера , а=2,07, следовательно нулевая гипотеза отвергается в пользу альтернативной и коэффициент регрессиистатистически значим, то есть наличие существенной линейной зависимости между количеством миль, проведенных в путешествии и величиной расходов статистически подтверждается.

Оценка статистической значимости построенной модели регрессии в целом производится с помощью F- критерия Фишера. Фактическое значение F-критерия качества оценивания регрессии, который представляет собой отношение объясненной суммы квадратов SSR (в расчете на одну независимую переменную) к остаточной сумме квадратов SSE (в расчете на одну степень свободы), определяется как:

,

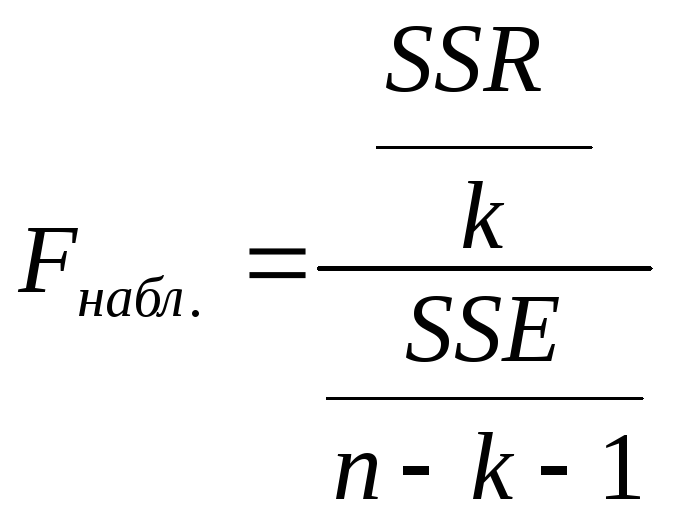где SSR =- факторная, или объясненная моделью регрессии, сумма квадратов,

- остаточная, или необъясненная моделью сумма квадратов

k - число независимых переменных.

F - критерий можно выразить через коэффициент детерминации:

.

Для определения табличного значения воспользуйтесь таблицами распределения Фишера-Снедекора для заданного уровня значимости α, принимая во внимание, что в случае парной регрессии число степеней свободы большей дисперсии равно 1, а число степеней свободы меньшей дисперсии равно n - 2.

Для нашего примера =671, 137, а=4,45. Так какпостроенная модель регрессии в целом значима и может в дальнейшем использоваться нами для прогнозов.

Для выполнения пункта 5 необходимо изучить вопрос об интервальном оценивании в регрессионном анализе, уяснить смысл понятий “точечный прогноз” и “интервальный прогноз”. Для расчета точечного прогноза подставьте в уравнение регрессии заданное значение факторного признака.

Так, например, если необходимо оценить расходы путешественника, преодолевшего (собирающегося преодолеть) 4500 миль, следует использовать уравнение регрессии записанное нами в пункте 2:

, то есть в среднем путешественник, преодолевший 4500 миль израсходует 5915,7215 условных денежных единиц.

Доверительный интервал для значений , лежащих на линии регрессии, имеет вид:

,

где

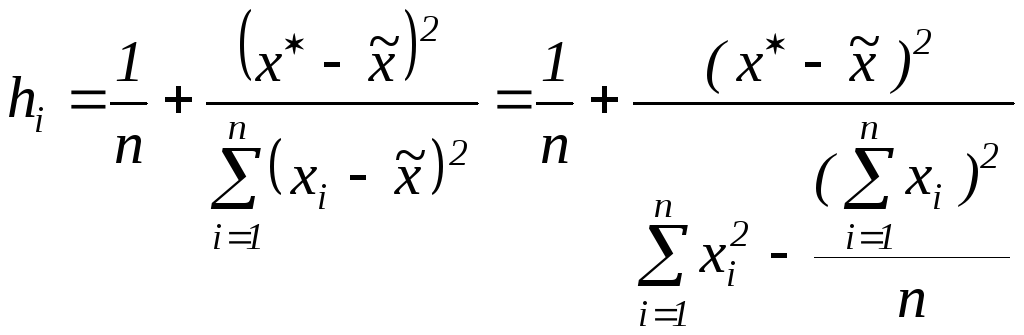
- прогнозное значение зависимой переменной;

- стандартная ошибка оценки;

n - объем выборки;

- заданное значение .

Полученный интервал будет характеризовать значения результативного признака при заданном значении факторного признака для отдельной наблюдаемой единицы.

Так, для нашего примера этот доверительный интервал будет выглядеть как 5247,83676582,9665, то есть с вероятностью 0,95 можно утверждать, что расходыодного путешественника, преодолевшего 4500 миль составят от 5247,8367 до 6582,9665 условных денежных единиц.

Если же необходимо сделать вывод об интервале значений результативного признака для всех наблюдаемых единиц при среднем значении факторного признака , расчет будет производиться по формуле доверительного интервала генерального значения:

.

В соответствии с условиями рассматриваемого примера доверительный интервал, характеризующий расходы всех путешественников, преодолевших 4500 миль будет выглядеть как 5730,9186099,885, то есть расходывсех путешественников, преодолевших расстояние в 4500 миль составят от 5730,918 до 6099,885 условных денежных единиц.

Сделайте выводы по задаче в целом.

Задача 2 составлена по теме “Множественная регрессия и корреляция” и предполагает построение и анализ двухфакторного уравнения линейной регрессии вида:

.

Рассмотрим методику решения задачи такого типа на примере:

Компания, производящая моющие средства, предприняла рекламную акцию в магазинах с демонстрацией антисептических свойств нового моющего средства. В этот же период компания использовала обычную теле- и радиорекламу. Через 20 недель компания решила проанализировать сравнительную эффективность различных видов рекламных расходов. Аналитик компании, исходя из гипотезы о линейной регрессионной взаимосвязи, оценил параметры модели следующего вида:

,

где

–объем продаж моющего средства,

–расходы на теле и радио рекламу,

–расходы на демонстрацию товара в магазинах.

Расходы приведены в условных денежных единицах.

Таблица 1. Исходные данные

Номера наблюдений
1	72	12	5
2	76	11	7
3	78	15	6
4	70	10	5
5	68	11	3
6	80	16	7
7	82	14	3
8	65	8	4
9	62	8	3
10	90	18	5

Пункт 1 посвящен анализу показателей тесноты связи в уравнении множественной регрессии.

Но прежде чем приступить к анализу показателей тесноты связи необходимо рассмотреть дискриптивные (описательные статистики), которые подробно изучались в курсах математической статистики с элементами теории вероятностей и общей теории статистики

Таблица 2. Дискриптивные статистики

	y	x1	x2
Размер выборки, n	10	10	10
Средняя арифметическая	74,3	12,3	4,8
Среднее квадратическое (стандартное) отклонение, S	8,54	3,37	1,55
Коэффициент вариации, V	0,12	0,27	0,32
Коэффициент асимметрии, As	0,35	0,31	0,19
Коэффициент эксцесса, Ex	-0,32	-0,91	-1,28

Сравнивая значения средних величин и стандартных отклонений, находим коэффициент вариации, значения которого свидетельствуют о том, что уровень варьирования признаков находится в допустимых пределах (< 0,35). Значения коэффициентов асимметрии и эксцесса указывают на отсутствие значимой скошенности и остро-(плоско-) вершинности фактического распределения признаков по сравнению с их нормальным распределением.⁴ По результатам анализа дискриптивных статистик можно сделать вывод, что совокупность признаков – однородна и для её изучения можно использовать метод наименьших квадратов (МНК) и вероятностные методы оценки статистических гипотез.

Парный коэффициент корреляции - это линейный коэффициент корреляции, характеризующий степень тесноты линейной связи между результативным и факторным признаками. Методика его расчета и интерпретация была изложена в пункте 3 задачи 1. При выполнении задания необходимо выписать матрицу парных коэффициентов корреляции и сделать выводы о наличии (отсутствии) в построенной модели мультиколлинеарности факторов.

Значения линейных коэффициентов парной корреляции представлены в матрице парных коэффициентов (таблица 3). Они определяют тесноту парных зависимостей между анализируемыми переменными.

Таблица 3.Парные коэффициенты линейной корреляции Пирсона

	1,0000 (0,0)	0,9393 (0,0001)	0,4167 (0,2310)
	0,9393 (0,0001)	1,0000 (0,0)	0,4174 (0,2301)
	0,4167 (0,2310)	0,4174 (0,2301)	1,0000 (0,0)
В скобках: P (

Коэффициент корреляции между исвидетельствует о значительной и статистически существенной линейной связи между объемом продаж моющего средства и расходами на радио и теле рекламу. Увеличение расходов на рекламу поднимает объем продаж. Связь междуине является статистически значимой. Кроме того, степень тесноты связи междуивыше, чем междуи. Таким образом, можно сделать предварительное заключение, что расходы на демонстрацию моющего средства в магазинах, существенно не влияют на рост объема продаж нового моющего средства.

Частные коэффициенты корреляции характеризуют тесноту связи между результативным и факторным признаками при фиксированном воздействии других факторов, включенных в уравнение регрессии. Их можно определить, используя парные коэффициенты корреляции по следующим рабочим формулам:

,

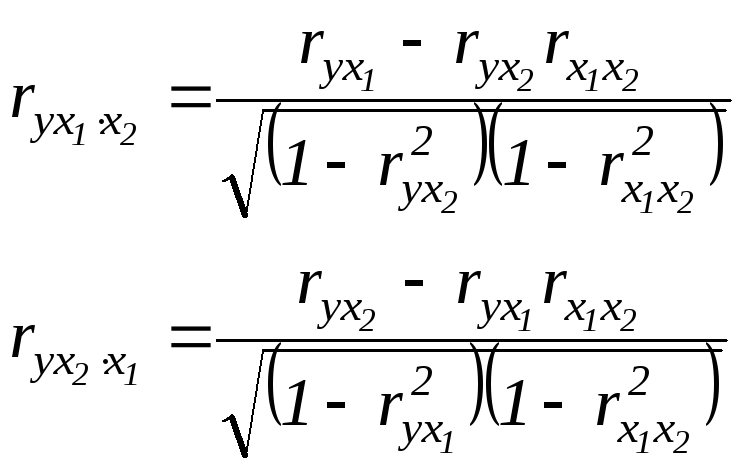где

- частный коэффициент корреляции между результативным и первым факторным признаками при фиксированном воздействии второго факторного признака,

- частный коэффициент корреляции между результативным и вторым факторным признаками при фиксированном воздействии первого факторного признака,

, ,- парные коэффициенты корреляции.

Интерпретируйте полученные значения частных коэффициентов корреляции и поясните причины различий между значениями частных и парных коэффициентов корреляции.

Приведенные в таблице 4 линейные коэффициенты частной корреляции оценивают тесноту связи значений двух переменных, исключая влияние всех других переменных, представленных в уравнении множественной регрессии.

Таблица 4. Коэффициенты частной корреляции

	1,0000 (0,0)	0,9265 (0,0003)	0,0790 (0,8399)
	0,9265 (0,0003)	1,0000 (0,0)	0,0834 (0,8311)
	0,0790 (0,8399)	0,0834 (0,8311)	1,0000 (0,0)
В скобках: P (

Коэффициенты частной корреляции дают более точную характеристику тесноты зависимости двух признаков, чем коэффициенты парной корреляции, так как «очищают» парную зависимость от взаимодействия данной пары переменных с другими переменными, представленными в модели. Наиболее тесно связаны и, . Другие взаимосвязи существенно слабее. При сравнении коэффициентов парной и частной корреляции видно, что из-за влияния межфакторной зависимости между ипроисходит некоторое завышение оценки тесноты связи между переменными.

По этой причине рекомендуется при наличии сильной коллинеарности (взаимосвязи) факторов исключать из исследования тот фактор, у которого теснота парной зависимости меньше, чем теснота межфакторной связи.

Пункт 2. Расчет параметров линейного уравнения множественной регрессии осуществляется обычным МНК путем решения системы нормальных уравнений. Для уравнения с двумя объясняющими переменными система примет вид:

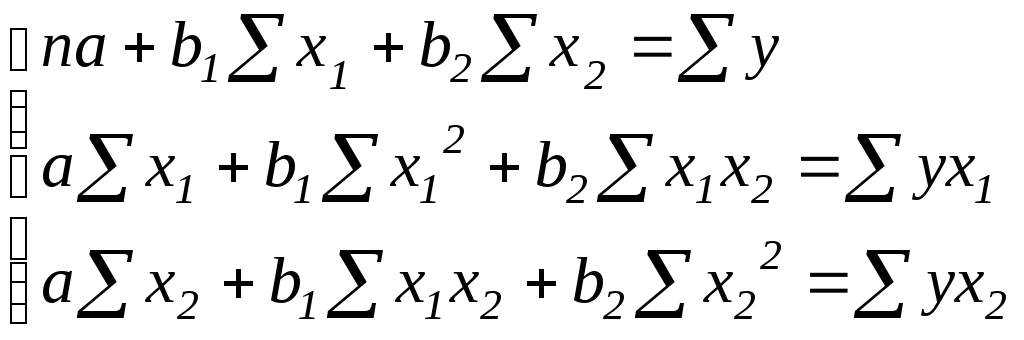
Поясните экономический смысл коэффициентов регрессии и: это показатели, характеризующие абсолютное (в натуральных единицах измерения) изменение результативного признака при изменении факторного признака на единицу своего измерения при фиксированном влиянии второго фактора.

Результаты построения уравнения множественной регрессии представлены в таблице 5.

Таблица 5. Результаты построения модели множественной регрессии

Независимые переменные		Коэффициенты	Стандартные ошибки коэффициентов		t - статистики	Вероятность случайного значения
Константа		44,61	4,58		9,73	0,0001
x1		2,35	0,36		6,51	0,0003
x2		0,16	0,78		0,21	0,8399
R2 = 0,88
R2adj=0,85
F = 26,402	Prob > F = 0,0005

Уравнение имеет вид:

y ₌ 44,61 + 2,35x₁ + 0,16x₂

Значения стандартной ошибки параметров представлены в графе 3 таблицы 5: Они показывают, какое значение данной характеристики сформировалось под влиянием случайных факторов. Их значения используются для расчета t-критерия Стьюдента (графа 4)

9,73; =6,51;=0,21.

В нашем примере параметр является статистически значимым, а- нет.⁵ На это же указывает значение вероятности случайных значений параметров регрессии (графа 5), если вероятность меньше принятого за стандарт уровня  = 0,05, то делается вывод о неслучайной природе данного значения параметра, то есть о том, что он статистически значим и надежен. В противном случае принимается нулевая гипотеза (H₀) о случайной природе значения коэффициентов уравнения. В нашем примере для переменной х₂  > 0,05 (_х2=0,84), что свидетельствует о малой информативности (значимости) этой переменной.

Интерпретация коэффициентов регрессии следующая:

а - оценивает агрегированное влияние прочих (кроме учтенных в модели х₁ и х₂) факторов на результат y;

и указывают, что с увеличением х₁ и х₂ на единицу их значений объем продаж нового моющего средства увеличивается, соответственно, на 2,35 и 0,16 условных денежных единиц.

Пункт 3 связан с расчетом и анализом относительных показателей силы связи в уравнении множественной регрессии - частных коэффициентов эластичности. Частные коэффициенты эластичности рассчитывают, как правило, для средних значений факторного и результативного признака:

,

где - коэффициент условно-чистой регрессии приj-м факторе,

- среднее значение j-го факторного признака;

- среднее значение результативного признака,

m - число факторных признаков в уравнении множественной регрессии.

Зачастую интерпретация результатов регрессии более наглядна, если произведен расчет частных коэффициентов эластичности. Частные коэффициенты эластичности показывают, на сколько процентов от значения своей среднейизменяется результат при изменении фактора x_j на 1% от своей средней и при фиксированном воздействии на y прочих факторов, включенных в уравнение регрессии. Здесь

По значениям частных коэффициентов эластичности можно сделать вывод о более сильном влиянии на результат у (объем продаж моющего средства) рекламной компании по радио и телевидению, нежели демонстрации товара в магазинах.

Пункт 4 предполагает оценку совокупного влияния факторных переменных на результативный признак.

Оцените долю вариации результативного признака, объясненную совокупным влиянием факторных признаков, рассчитав совокупный (нескорректированный) множественный коэффициент детерминации:

,

где SSR=- факторная, или объясненная моделью регрессии, сумма квадратов,

SST =- общая сумма квадратов,

- остаточная, или не объясненная моделью регрессии сумма квадратов.

В нашем примере эта доля составляет 88,29% и указывает на весьма высокую степень обусловленности вариации результата вариацией факторов. Иными словами, на весьма тесную связь факторов с результатом.

Скорректированный множественный коэффициент детерминации

(где n – число наблюдений, m – число объясняющих переменных) определяет тесноту связи с учетом степеней свободы общей и остаточной дисперсий. Он дает такую оценку тесноты связи, которая не зависит от числа факторов в модели и поэтому может сравниваться по разным моделям с разным числом факторов. Оба коэффициента указывают на весьма высокую детерминированность результата y в модели факторами x₁ и x₂.

Охарактеризуйте степень тесноты связи между результативным признаком и всеми факторными, включенными в уравнение регрессии, определив множественный коэффициент корреляции:

.

Пункт 5 предполагает ознакомление с методикой дисперсионного анализа по модели множественной регрессии.

Проверьте статистическую значимость модели регрессии в целом с помощью F-критерия Фишера. Для этого воспользуйтесь алгоритмом проверки гипотез, изложенном в указаниях к пункту 4 задачи 1, учитывая, что фактическое значение F – критерия для уравнения множественной регрессии определяется по формуле:

,

где k - общее число параметров в уравнении множественной регрессии (в случае двухфакторной линейной регрессии k = 3).

Для проведения дисперсионного анализа и расчета фактического значения F - критерия рекомендуется также заполнить таблицу результатов дисперсионного анализа:

Колеблемость результативного признака	Сумма квадратов	Число степеней свободы	Дисперсия	F-критерий
За счет регрессии	Сфакт. (SSR)	k	(MSR)
Остаточная	Сост. (SSE)	n-(k+1)	(MSE)
Общая	Собщ. (SST)	n-1

Для нашего примера:

Таблица 6. Дисперсионный анализ модели множественной регрессии

Колеблемость результативного признака	Сумма квадратов	Число степеней свободы	Дисперсия	F-критерий
За счет регрессии	579,303	2	289,651	26,402
Остаточная	76,797	7	10,971
Общая	656,100	9

Оценку надежности уравнения регрессии в целом, его параметров и показателя тесноты связи дает F-критерий Фишера :

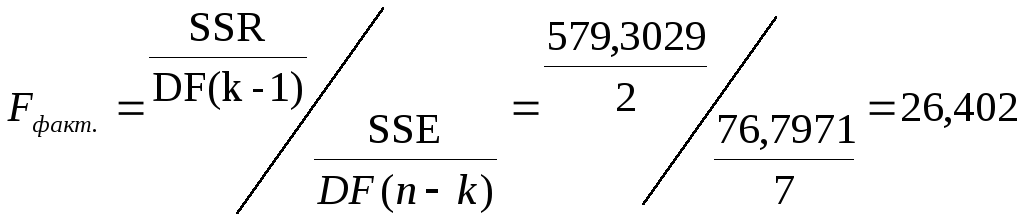
Вероятность случайного значения F - критерия = 24,402 составляет 0,0005, что значительно меньше 0,05. Следовательно, полученное значение неслучайно, оно сформировалось под влиянием существенных факторов. То есть подтверждается статистическая значимость всего уравнения, его параметров и показателя тесноты связи – коэффициента множественной корреляции.

Общий вывод по построенной регрессионной модели состоит в том, что на увеличение объёма продаж нового моющего средства значимо повлияла реклама на радио и телевидении: при увеличении расходов на рекламу – возрастал объем продаж. Затраты же на демонстрацию моющего средства в магазинах не оказали существенного влияния на рост объёма продаж.

Прогноз по модели множественной регрессии осуществляется по тому же принципу, что и для парной регрессии. Для получения прогнозных значений мы подставляем значения х_i в уравнение для получения значения. Предположим, что мы хотим узнать ожидаемый объем продаж моющего средства, при условии, что затраты на теле и радио рекламу составят 10 условных денежных единиц, а на демонстрацию в магазинах – 5 денежных единиц.

(денежных единиц).

Качество прогноза – неплохое, поскольку в исходных данных таким значениям независимых переменных соответствует значение равное 70 денежных единиц.

Мы так же можем вычислить интервал прогноза как - доверительный интервал для ожидаемого значенияпри заданных значениях независимых переменных:

,

где MSE – остаточная дисперсия, а стандартная ошибка для случая нескольких независимых переменных имеет достаточно сложное выражение, которое мы здесь не приводим.доверительный интервал для значенияпри средних значениях независимых переменных имеет вид:Большинство пакетов программ рассчитывают доверительные интервалы автоматически.

Задачи 3, 4 и 5посвящены теме “Временные ряды в эконометрических исследованиях”, и, прежде всего проблеме автокорреляции уровней временного ряда и ее последствиям, а также наличию во временном ряде тенденции.

Задача 3.

Рассмотрим методику решения задачи на практическом примере:

Имеются следующие данные о расходах семьи на товар "А" в 1994-1999 гг.:

Годы	1994	1995	1996	1997	1998	1999
Расходы на товар "А", руб.	30	35	39	44	50	53

Приступая к выполнению пункта 1, изучите вопрос об измерении автокорреляции уровней временного ряда.

Коэффициент автокорреляции первого порядка есть линейный коэффициент корреляции между уровнями исходного временного ряда и уровнями того же ряда сдвинутыми на один момент времени.

Его расчет производится по стандартным формулам для расчета линейного коэффициента корреляции:

,

где y_{t - 1} - уровни, сдвинутые по отношению к уровням исходного ряда на 1 год.

Заметим, что расчет должен быть осуществлен для пар наблюдений (,, причем общее число пар наблюдений, по которым производится расчет, равно (n - 1). Близкое по абсолютной величине к единице значение коэффициента автокорреляции первого порядка свидетельствует о высокой тесноте связи между текущими и непосредственно предшествующими уровнями временного ряда или, иными словами, о наличии во временном ряде тенденции.

В соответствии с условиями нашей задачи проведем расчеты

	yt	yt+1	ytyt+1	yt2	yt+12
1994	30	35	1050	900	1225
1995	35	39	1365	1225	1521
1996	39	44	1716	1521	1936
1997	44	50	2200	1936	2500
1998	50	53	2650	2500	2809
Суммы	198	221	8981	8082	9991

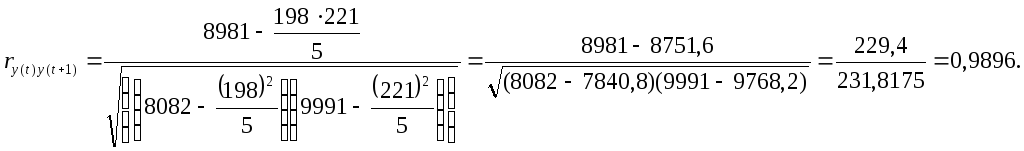
Коэффициент автокорреляции первого порядка равен 0,9896, что свидетельствует о тесной прямой связи между текущими и непосредственно предшествующими уровнями временного ряда.

В пункте 2 требуется определить функциональную форму и найти параметры уравнения, наилучшим образом описывающего тенденцию (тренд). Для определения вида тренда рассчитайте следующие показатели динамики:

а) цепные абсолютные приросты: ;

б) абсолютные ускорения уровней ряда, или вторые разности: ;

в) цепные коэффициенты роста: .

Проанализируйте полученные результаты.

Если приблизительно одинаковы цепные абсолютные приросты, то для описания тенденции временного ряда следует выбрать линейный тренд: .

Если примерно постоянны абсолютные ускорения уровней ряда, следует выбрать параболу второго порядка: .

Если примерно одинаковы цепные коэффициенты роста, моделирование тенденции следует проводить с использованием экспоненциальной кривой: .

Для расчета параметров уравнения тренда примените обычный МНК. В случае нелинейных зависимостей проведите линеаризацию исходной функции.

Дайте интерпретацию параметров тренда.

Коэффициент регрессии b в линейном тренде есть средний за период цепной абсолютный прирост уровней ряда.

В экспоненциальной функции величина представляет собой средний за период цепной темп роста уровней ряда.

Начальный уровень ряда в момент (период времени) t = 0 в линейном тренде выражается параметром а, в экспоненциальном тренде - величиной .

Для нашей задачи проведем следующие расчеты:.

	yt
1994	30
1995	35	5		1,1667
1996	39	4	-1	1,1143
1997	44	5	1	1,1282
1998	50	6	1	1,1364
1999	53	3	-3	1,0600

Очевидно, в данном случае для описания тренда можно выбрать линейную модель: .

Для расчета параметров уравнения тренда применим обычный МНК.

Если периоды или моменты времени пронумеровать так, чтобы получилось t =0, то вышеприведенные алгоритмы существенно упростятся и превратятся в

Расчеты проведем в следующей рабочей таблице.

	t	yt	t2	ytt
1994	-2,5	30	6,25	-75
1995	-1,5	35	2,25	-52,5
1996	-0,5	39	0,25	-19,5
1997	0,5	44	0,25	22
1998	1,5	50	2,25	75
1999	2,5	53	6,25	132,5
Суммы	0,00	251	17,5	82,5

Таким образом, трендовое линейное уравнение регрессии имеет вид:

.

Дадим интерпретацию параметров тренда.

Коэффициент регрессии (b) в линейном тренде показывает средний за период цепной абсолютный прирост уровней ряда. В нашем примере b = 4,7143, следовательно расходы на товар "А" в среднем за год увеличиваются на 4,7143 руб. Свободный член (а) в линейном тренде выражает начальный уровень ряда в момент (период времени) t = 0. В нашей нумерации t = 0 приходится на период времени между 1996 и 1997 гг., что несколько затрудняет его интерпретацию. В нашем случае а = 41,8333 руб. – это расходы семьи на товар "А" за вторую половину 1996 и первую половину 1997 гг.

В случае нелинейных зависимостей необходимо провести линеаризацию исходной функции.

Пункт 3. Точечный прогноз по уравнению тренда - это расчетное значение переменной , полученное путем подстановки в уравнение тренда соответствующих значенийt. Интервальный прогноз рассчитывается в соответствии с методикой, изложенной для уравнения парной линейной регрессии (см. указания к пункту 5 задачи 1).

Дадим прогноз расходов на товар "А" на 2000 год.

В нашей нумерации 2000 год соответствует моменту времени t = 3,5. Отсюда,

Следовательно, точечная оценка расходов семьи на товар "А" на 2000 год составляет 58,3333 руб.

Определим границы доверительного интервала, в котором с заданной надежностью γ будут находится расходы семьи на товар "А" в 2000 году. Общепринятый в экономике уровень надежности γ = 1 - α = 1 - 0,05 = 0,95.

,

где -прогноз значения переменнойy на момент (период) времени t;

- точечная оценка значения переменной y на момент (период) времени t;

- предельная ошибка прогноза.

Для того, чтобы получить интервальную оценку, определим величину предельной ошибки прогноза.

Она рассчитывается по формуле:

,

где - табличное значение t - критерия Стьюдента для уровня значимостиα и числа степеней свободы (k = n - 2);

- стандартная ошибка точечного прогноза, которая, в свою очередь, рассчитывается по формуле:

,

где - длина периода упреждения (срок прогноза).

Расчеты проведем в рабочей таблице.

	t
1994	-2,5	30	30,0476	-0,0476	0,0023
1995	-1,5	35	34,7619	0,2381	0,0567
1996	-0,5	39	39,4762	-0,4762	0,2268
1997	0,5	44	44,1905	-0,1905	0,0363
1998	1,5	50	48,9048	1,0952	1,1995
1999	2,5	53	53,6190	-0,6190	0,3832
Суммы	0,00	251	197,3810	0,0000	1,9048

Табличное значение t - критерия Стьюдента для уровня значимости α = 0,05 и числа степеней свободы k = 6 – 2 = 4 составляет 2,78, т.е. =2,78.

Отсюда,

Таким образом,

;

.

С вероятностью 0,95 можно ожидать, что в 2000 году расходы семьи на товар "А" будут находиться в пределах от 55,4089 до 61,2577 руб.

Обратите внимание на то, что приведенные формулы верны только для уравнения парной регрессии, линейной по параметрам.

Задача 4.

Рассмотрим методику решения задачи на примере:

Имеются следующие данные о величине дохода в расчете на одного члена семьи в процентах к 1994 году и о расходах семьи на товар "А" в 1994-1999 гг.:

Годы	1994	1995	1996	1997	1998	1999
Расходы на товар "А", руб.	30	35	39	44	50	53
Доход на одного члена семьи в процентах к 1994 году, %	100	103	105	109	115	118

Пункт 1. Определение функциональной формы трендового уравнения регрессии описано в пункте 2 к задаче 3.

Пункты 2-3. При измерении корреляции между двумя временными рядами следует учитывать возможность наличия ложной корреляции, обусловленной простым сопутствием временных рядов. Для того чтобы устранить ложную корреляцию, следует определять степень тесноты связи не самих уровней временных рядов, а их последовательных (первых или вторых) разностей или отклонений от трендов (если последние не содержат тенденции).

Сделайте вывод о наличии или отсутствии ложной корреляции при разных способах измерения связи между исследуемыми временными рядами, поясните причины существования ложной корреляции.

По данным примера рассчитаем коэффициент корреляции между расходами на товар "А" и доходом на одного члена семьи по исходным уровням ряда:

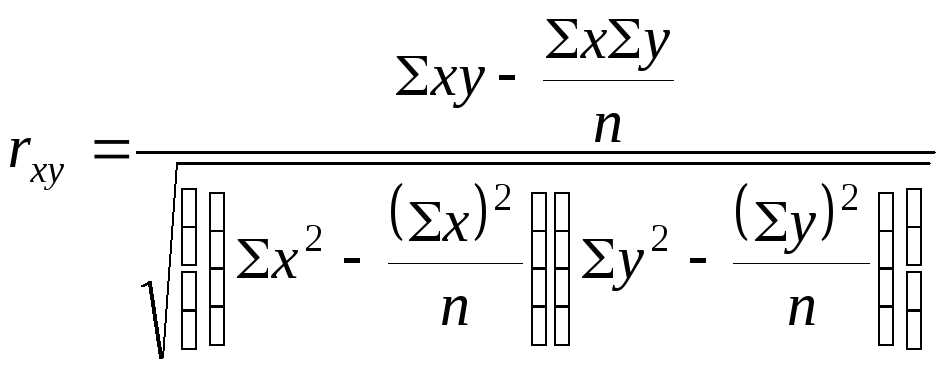
Заметим, что расчет может быть осуществлен и по другим формулам.

Промежуточные расчеты проведем в рабочей таблице.

Годы	y	x	xy	y2	x2
1994	30	100	3000	900	10000
1995	35	103	3605	1225	10609
1996	39	105	4095	1521	11025
1997	44	109	4796	1936	11881
1998	50	115	5750	2500	13225
1999	53	118	6254	2809	13924
Суммы	251	650	27500	10891	70664

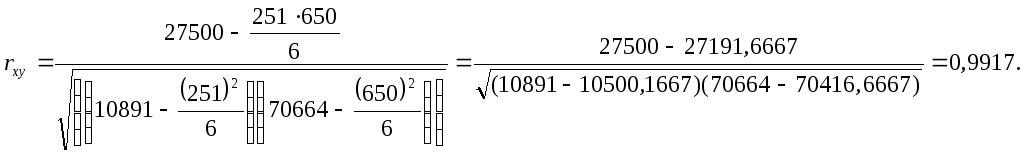
Близкое к единице значение коэффициента корреляции свидетельствует о тесной прямой связи между расходами на товар "А" и доходом на одного члена семьи.

Однако, учитывая, что расчет был произведен по уровням временного ряда, корреляция между изучаемыми признаками может быть вызвана простым сопутствием явлений во времени.

Для того, чтобы исключить тенденцию, рассчитаем коэффициент корреляции по первым разностям.

Промежуточные расчеты проведем в рабочей таблице.

Годы	y	x	Δy	Δx	ΔxΔy	Δy2	Δx2
1994	30	100
1995	35	103	5	3	15	25	9
1996	39	105	4	2	8	16	4
1997	44	109	5	4	20	25	16
1998	50	115	6	6	36	36	36
1999	53	118	3	3	9	9	9
Суммы	251	650	23	18	88	111	74

.

.

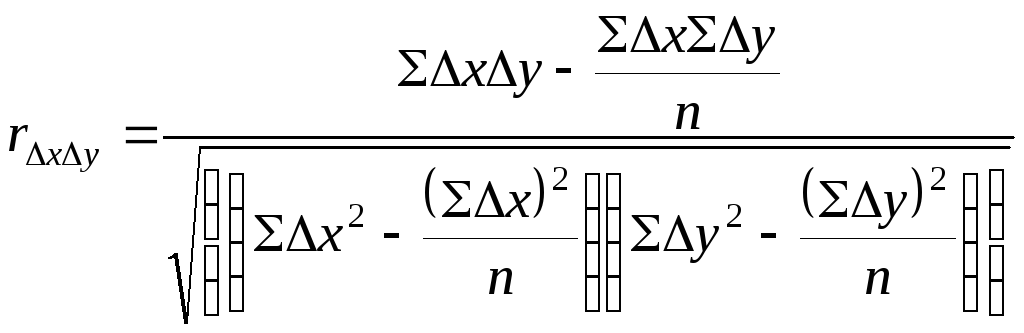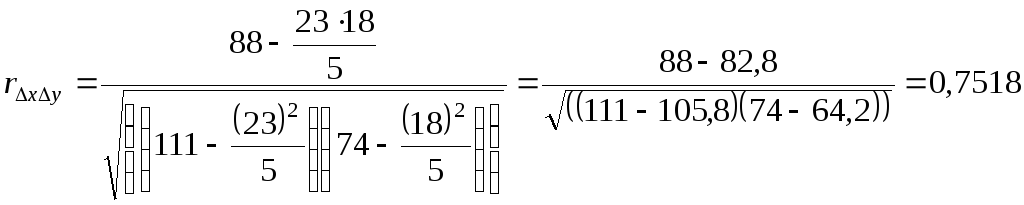Коэффициент корреляции между расходами на товар "А" и доходом на одного члена семьи, рассчитанный по первым разностям, показывает не столь тесную связь, как коэффициент, рассчитанный по уровням ряда динамики.

Расчет коэффициента корреляции по первым разностям позволяет устранить тенденцию, зависимость между x и y, обусловленную сопутствием рядов во времени.

Рассчитаем коэффициент корреляции между расходами на товар "А" и доходом на одного члена семьи по отклонениям от тренда.

Прежде, чем рассчитывать отклонения от тренда, определим функциональную форму трендовых уравнений регрессии расходов на товар "А" и дохода на одного члена семьи.

Слабая колеблемость первых разностей (цепных абсолютных приростов) позволяет говорить о линейной форме обеих моделей.

Трендовое линейное уравнение регрессии расходов на товар "А" имеет вид (расчеты см. в методических указаниях к решению задачи 3):

.

Аналогично рассчитаем параметры трендового линейного уравнения регрессии доходов в расчете на одного члена семьи:

Годы	t	x	xt	t2
1994	-2,50	100	-250	6,25
1995	-1,5	103	-154,5	2,25
1996	-0,5	105	-52,5	0,25
1997	0,5	109	54,5	0,25
1998	1,5	115	172,5	2,25
1999	2,5	118	295	6,25
Суммы	0	650	65	17,5

Таким образом, трендовое линейное уравнение регрессии имеет вид:

.

Перейдем к расчету коэффициента корреляции по отклонению от тренда согласно формуле:

1994	30	30,0476	-0,0476	0,0023	100	99,0476	0,9524	0,9070	-0,04535
1995	35	34,7619	0,2381	0,0567	103	102,7619	0,2381	0,0567	0,056689
1996	39	39,4762	-0,4762	0,2268	105	106,4762	-1,4762	2,1791	0,702948
1997	44	44,1905	-0,1905	0,0363	109	110,1905	-1,1905	1,4172	0,226757
1998	50	48,9048	1,0952	1,1995	115	113,9048	1,0952	1,1995	1,199546
1999	53	53,6190	-0,6190	0,3832	118	117,6190	0,3810	0,1451	-0,23583
Суммы	251	197,3810	0,0000	1,9048	650	532,3810	0,0000	5,90476	1,90476

.

Величина этого коэффициента корреляции еще более убедительно свидетельствует о сопутствии рядов во времени.

Пункт 4. По аналогии с коэффициентами корреляции параметры уравнения регрессии по временным рядам определяют также не по исходным их уровням, а по последовательным разностям, либо отклонениям от тренда.

Обратите внимание на интерпретацию параметров, полученных уравнений регрессии:

- если уравнение регрессии построено по первым разностям, то коэффициент регрессии b характеризует изменение прироста результативного признака при изменении прироста факторного признака на единицу.

Сделайте общий вывод о наличии и тесноте причинно-следственной связи между изучаемыми временными рядами, укажите ее направление.

Определим параметры уравнения парной линейной регрессии по первым разностям.

Расчет осуществляется обычным методом наименьших квадратов:

Годы	y	x	Δy	Δx	ΔxΔy	Δy2	Δx2
1994	30	100
1995	35	103	5	3	15	25	9
1996	39	105	4	2	8	16	4
1997	44	109	5	4	20	25	16
1998	50	115	6	6	36	36	36
1999	53	118	3	3	9	9	9
Суммы	251	650	23	18	88	111	74

Отсюда, модель имеет вид:

Коэффициент регрессии b = 0,5652 означает, что с изменением прироста душевого дохода на 1 процентный пункт расходы на товар "А" изменяются с ускорением, равным 0,5652 руб.

Задача 5 посвящена методике выявления сезонной компоненты в рядах динамики, построению моделей с аддитивной и мультипликативной сезонными компонентами и прогнозированию по этим моделям.

Для выявления тренда и наличия сезонной компоненты постройте график ряда динамики (пункт 1). При построении графика ряда динамики по оси абсцисс откладываются временные промежутки, а по оси ординат – уровни ряда.

Приступая к выполнению пункта 2, изучите вопрос об особенностях анализа сезонных колебаний.

Сезонная колеблемость в рядах динамики может иметь аддитивный и мультипликативный характер.

Если сезонная вариация постоянна в различных временных периодах, то для анализа временного ряда подходит модель с аддитивной компонентой.

Если сезонная вариация не является константой, например, увеличивается с возрастанием значений тренда, то для анализа лучше подходит модель с мультипликативной компонентой, в которой значения сезонной компоненты представляют собой определенную долю трендового значения.

В зависимости от особенностей сезонной вариации сделайте выбор между моделями с аддитивной и мультипликативной компонентами.

Каждой из этих моделей соответствуют различные методы расчета сезонной компоненты тренда, использующие сочетание методов скользящего среднего и линейной регрессии.

Следует помнить, что поскольку сезонные колебания характеризуются относительно небольшими временными интервалами, то прогнозирование по моделям с сезонной компонентой – также краткосрочное.

Модель с аддитивной компонентой. Если сезонная компонента переменной А – постоянна, модель фактических значений переменной А можно представить следующим образом:

Фактическое значение =

= Трендовое значение + Сезонная вариация + Ошибка,

то есть:

A = T + S + E.

Модель с мультипликативной компонентой. Если значение сезонной компоненты переменной А, не является константой, а представляет собой определенную долю трендового значения, т.е. значения сезонной компоненты увеличиваются с возрастанием значений тренда, модель фактических значений переменной А можно представить следующим образом:

Фактическое значение =

= Трендовое значение Сезонная вариацияОшибка,

т.е.

А = T SE.

В моделях, как с аддитивной, так и с мультипликативной компонентой общая процедура анализа примерно одинакова:

Шаг 1. Расчет значений сезонной компоненты.

Шаг 2. Десезонализация данных. Для модели с аддитивной компонентой он состоит в вычитании сезонной компоненты из фактических значений. Для модели с мультипликативной компонентой – в расчете отношений между фактическими значениями и сезонной составляющей. Расчет тренда на основе полученных десезонализированных данных.

Шаг 3. Расчет ошибок как разности между фактическими и трендовыми значениями. В мультипликативной модели можно рассчитать ошибки еще и как отношение между фактическими и трендовыми значениями.

Шаг 4. Расчет среднего линейного отклонения или среднеквадратической ошибки для обоснования соответствия модели исходным данным или для выбора из множества моделей наилучшей.

Для того чтобы элиминировать влияние сезонной компоненты (пункт 3) воспользуйтесь методом скользящей средней. Если сезон состоит из 4-х кварталов (год), следует провести сглаживание по 4-м точкам, если сезон состоит из 7-и дней (неделя) следует провести сглаживание по 7-и точкам и т.д.

Значения уровней ряда, сглаженные по четному числу точек необходимо центрировать.

Множество скользящих средних представляет наилучшую оценку искомого тренда.

Процедуры сглаживания и центрирования одинаковы при построении моделей с аддитивной и мультипликативной компонентами.

Полученные значения тренда используйте для нахождения оценок сезонной компоненты.

Для модели с аддитивной компонентой:

A – T = S + E.

Для модели с мультипликативной компонентой:

А/Т= S E.

Найдите средние значения сезонных оценок для каждого года (недели и т.п.). Эта процедура позволяет уменьшить некоторые значения ошибок.

Скорректируйте средние значения.

Для модели с аддитивной компонентой корректировка состоит в увеличении или уменьшении средних значений на одно и то же число таким образом, чтобы их общая сумма была равна нулю. Это необходимо для того, чтобы усреднить значения сезонной компоненты в целом за период. Обычно корректирующий фактор рассчитывается путем деления суммы оценок сезонных компонент на число сезонов.

В мультипликативной модели значения сезонной компоненты - это относительные величины. Поэтому необходимо, чтобы их сумма была равна числу сезонов, а не нулю, как в случае с аддитивной моделью. Если это не так, произведите корректировку значений сезонной компоненты.

Шаг 2 состоит в десезонализации исходных данных (пункт 4).

В модели с аддитивной компонентой она заключается в вычитании соответствующих значений сезонной компоненты из фактических значений данных за каждый квартал (день и т.п.), то есть:

A – S = T + E.

В модели с мультипликативной компонентой процедура десезонализации осуществляется по формуле:

А/S= T E.

Новые оценки тренда, которые все еще содержат ошибку, используйте для построения модели основного тренда. Нанесите эти значения на исходную диаграмму, сделайте вывод о наличии тренда.

Пункт 5 посвящен подбору уравнения тренда с аддитивной или мультипликативной компонентой. При этом выбор функциональной формы тренда осуществляется, исходя из общих принципов, изложенных в пункте 2 к задаче 3.

Предположим, например, что тренд – линейный.

Уравнение линейного тренда имеет вид:

,

где х – порядковый номер квартала,

а и b – параметры уравнения парной регрессии.

Поскольку предполагается, что тренд имеет линейный характер, то значения параметров линии, аппроксимирующей тренд, найдите методом наименьших квадратов:

где y = T + E,

,

.

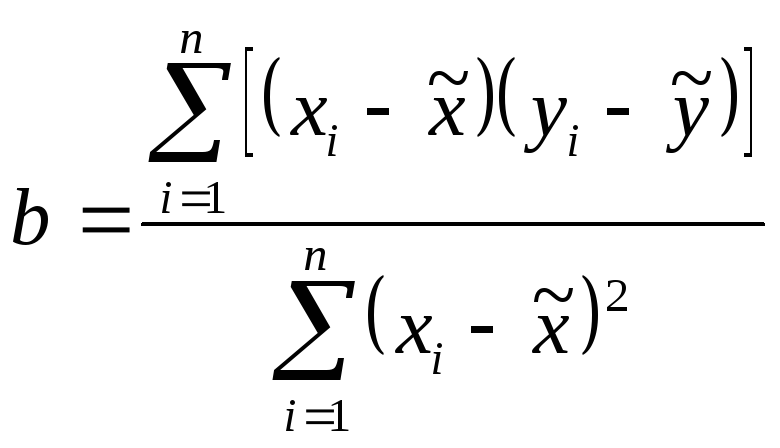Пункт 6 заключается в расчете ошибки (Е), среднего абсолютного отклонения (MAD) и среднеквадратической ошибки (MSE) модели.

Расчет этих показателей соответствует шагу 3 алгоритма и предшествует составлению прогноза.

Осуществите расчет ошибок или остатка.

В аддитивной модели он осуществляется по формуле:

Е = А - S - Т.

В мультипликативной:

Е = А/(Т S)

или

Е = А - (Т S).

Найдите меру соответствия модели исходным данным, т.е. определите ту часть колеблемости уровней ряда, которую невозможно объяснить с помощью построенной модели.

Для этого используйте среднее абсолютное отклонение (mean absolute deviation - MAD) и среднеквадратическую ошибку (mean square error - MCE):

;

.

Целесообразно использовать обе меры, так как последняя из них резко возрастает при наличии высоких ошибок.

Пункт 7 состоит в прогнозировании на основании полученных моделей.

Прогнозные значения по модели с аддитивной компонентой рассчитайте по формуле:

F = T + S.

В модели с мультипликативной компонентой используйте следующий алгоритм:

F= ТS.

Не следует забывать: чем более отдаленным является период упреждения, тем меньшей оказывается обоснованность прогноза.

Рассмотрим практическую реализацию методики решения задачи для модели с аддитивной компонентой.

В таблице 1 представлено количество продукции, проданной компанией FORA LTD в течение последних 13 кварталов.

Таблица 1. Количество продукции, проданной в течение последних 13 кварталов

ДАТА	Количество проданной продукции, тыс. шт.
Январь - март 1996	239
Апрель – июнь	201
Июль – сентябрь	182
Октябрь – декабрь	297
Январь - март 1997	324
Апрель – июнь	278
Июль – сентябрь	257
Октябрь – декабрь	384
Январь - март 1998	401
Апрель – июнь	360
Июль – сентябрь	335
Октябрь – декабрь	462
Январь - март 1999	481

Построим график, позволяющий сделать выводы о типе модели:

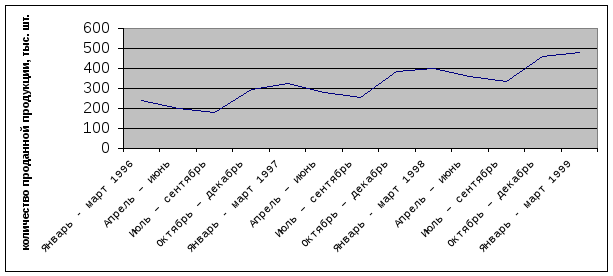
Стабильность сезонной компоненты указывает на то, что модель с аддитивной компонентой подходит для анализа этого временного ряда. То есть фактические объемы продаж можно выразить следующим образом:

A = T + S + E

Для того чтобы элиминировать влияние сезонной компоненты воспользуемся методом скользящей средней, которую рассчитаем с интервалом в три месяца. Этот расчет и все последующие проведем в таблице 2.

Таблица 2 . Расчет по 4 точкам центрированных скользящих средних значений тренда для модели A – T = S + E

ДАТА	Объем продаж, тыс.шт.	Итого за 4 квартала	Скользящая средняя за 4 квартала	Центрированная скользящая средняя	Оценка сезонной компоненты A-T=S+E
Январь - март 1996	239
Апрель – июнь	201
		919	229,75
Июль – сентябрь	182			240,4	-58,4
		1004	251
Октябрь – декабрь	297			260,6	+36,4
		1081	270,25
Январь - март 1997	324			279,6	+44,4
		1156	289
Апрель – июнь	278			299,9	-21,9
		1243	310,75
Июль – сентябрь	257			320,4	-63,4
		1320	330
Октябрь – декабрь	384			340,3	+43,8
		1402	350,5
Январь - март 1998	401			360,2	+40,8
		1480	370
Апрель – июнь	360			379,8	-19,8
		1558	389,5
Июль – сентябрь	335			399,5	-64,5
		1638	409,5
Октябрь – декабрь	462
Январь - март 1999	481

Просуммировав первые 4 значения, получим общий объем продаж в 1996 году. Разделив эту сумму на 4, найдем средний объем продаж в каждом квартале 1996 года:

(239 + 201 + 182 + 297)/4 = 299,75.

Полученное значение уже не содержит сезонной компоненты, так как представляет собой среднюю величину за год. У нас появилась оценка значения тренда для середины года, то есть для точки, лежащей в середине между кварталами II и III. Последовательно продвигаясь вперед с шагом в один квартал, рассчитаем средние квартальные значения для промежутков: апрель 1996 – март 1997 (251), июль 1996 – июнь 1997 (270,25) и т.д. Данная процедура позволяет генерировать скользящие средние по 4 точкам исходного множества данных. Получаемое таким образом множество скользящих средних представляет собой наилучшую оценку искомого тренда.

Теперь полученные значения тренда можно использовать для нахождения оценок сезонной компоненты. Мы рассчитываем:

A – T = S + E.

К сожалению, оценки значений тренда, получаемые в результате расчета скользящих средних по 4 точкам, относятся к несколько иным моментам времени, чем фактические данные. Первая оценка, равная 229,75, представляет собой точку, совпадающую с серединой 1996 года, то есть лежит в центре промежутка фактических объемов продаж во II и III кварталах. Вторая оценка, равная 251, лежит между фактическими значениями в III и IV кварталах. Нам же необходимы десезонализированные средние значения, соответствующие тем же интервалам времени, что и фактические значения за квартал. Положение десезонализированных средних во времени сдвигается путем дальнейшего расчета средних для каждой пары значений. Найдем среднюю из первой и второй оценок, центрируя их июнь-сентябрь 1996 года, т.е.

(229,75 + 251)/2 = 240,4.

Это и есть десезонализированная средняя за июль-сентябрь 1996 г. Эту десезонализированную величину, которая называется центрированной скользящей средней, можно непосредственно сравнивать с фактическим значением за июль-сентябрь 1996 года, равным 182. Отметим, что сглаживание по 4-м точкам приводит к потере оценок тренда за первые два или последние два квартала временного ряда.

После расчетов в таблице 2. мы имеем оценки сезонной компоненты, которые включают в себя ошибку или остаток. Прежде чем мы сможем использовать сезонную компоненту, нужно пройти два следующих этапа. Найдем средние значения сезонных оценок для каждого сезона года. Расчеты приведены в таблице 3.

Таблица 3. Расчет средних значений сезонной компоненты

		Номер квартала
	ГОД	1	2	3	4
	1996 1997 1998	- +44,4 +40,8	- -21,9 -19,8	-58,4 -63,4 -64,5	+36,4 43,8 -
Итого		+85,2	-41,7	-186,3	+80,2
Среднее значение		85,2  2	-41,7  2	-186,3  3	80,2  2
Оценка сезонной компоненты		+42,6	-20,8	-62,1	+40,1	Сумма=- 0,2
Скорректированная сезонная компонента		+42,6	-20,7	-62,0	+40,1	Сумма = 0

Эта процедура позволяет уменьшить некоторые значения ошибок. Наконец, скорректируем средние значения, увеличивая или уменьшая их на одно и то же число таким образом, чтобы их общая сумма была равна нулю. Это необходимо, чтобы усреднить значения сезонной компоненты в целом за год. Обычно корректирующий фактор рассчитывается путем деления суммы оценок сезонных компонент на число сезонов. В нашем же примере оценки второго и третьего кварталов мы округлили до ближайшего большего числа.

Значения скорректированной сезонной компоненты подтверждают наши выводы, сделанные на основе диаграммы. Объемы продаж за два зимних месяца превышают среднее трендовое значение приблизительно на 40 тыс. шт., а объемы продаж за два летних месяца ниже средних на 21 и 62 тыс. шт. соответственно.

Аналогичная процедура применима при определении сезонной вариации за любой промежуток времени. Если, например, в качестве сезона выступают дни недели, для элиминирования влияния ежедневной “сезонной компоненты” также рассчитывают скользящую среднюю, но уже не по четырем, а по семи точкам. Эта скользящая средняя представляет собой значение тренда в середине недели, то есть в четверг, таким образом, необходимость в центрировании отпадает.

Шаг 2 состоит в десезонализации исходных данных. Она заключается в вычитании соответствующих значений сезонной компоненты из фактических значений данных за каждый квартал, то есть A – S = T + E, что показано в таблице 4.

Таблица 4 . Расчет десезонализированных данных

ДАТА	Номер квартала	Объем продаж, тыс.шт.	Сезонная компонента	Десезонализированный объем продаж, Тыс. шт. A – S = T + E
Январь - март 1996	1	239	+42,6	196,4
Апрель – июнь	2	201	-20,7	221,7
Июль – сентябрь	3	182	-62,0	244,0
Октябрь – декабрь	4	297	+40,1	256,9
Январь - март 1997	5	324	+42,6	281,4
Апрель – июнь	6	278	-20,7	298,7
Июль – сентябрь	7	257	-62,0	319,0
Октябрь – декабрь	8	384	+40,1	343,9
Январь - март 1998	9	401	+42,6	358,6
Апрель – июнь	10	360	-20,7	380,7
Июль – сентябрь	11	335	-62,0	397,1
Октябрь – декабрь	12	462	+40,1	421,9
Январь - март 1999	13	481	+42,6	438,4

Новые оценки тренда, которые все еще содержат ошибку, можно использовать для построения модели основного тренда. Если нанести эти значения на исходную диаграмму, то можно сделать вывод о существовании явного линейного тренда

Уравнение линии тренда имеет вид:

,

где х – порядковый номер квартала,

а и b – параметры уравнения парной регрессии. Поскольку мы нашли, что тренд имеет линейный характер, то значения параметров линии, аппроксимирующей тренд, найдем методом наименьших квадратов.

где y = T + E,

, .

Подставив значения из последних колонок таблицы 4 в соответствующие формулы, получим: ,.

Следовательно, уравнение модели тренда имеет следующий вид (с округлением значений коэффициентов регрессии до ближайших целых значений):

Трендовое значение объема продаж, тыс. шт. = 180,0 + 20,0 * номер квартала.

Шаг 3 нашего алгоритма, предшествующий составлению прогноза состоит в расчете ошибок или остатка. Наша модель имеет следующий вид:

A = T + S + E.

Значение S было найдено в таблице 2, а значение T в таблице 3. Вычитая каждое значение из фактических объемов продаж, получим значения ошибок.

Таблица 5. Расчет ошибок для модели с аддитивной компонентой

Дата	Номер квартала	Объем продаж, Тыс. шт.	Сезонная компонента	Трендовое значение, тыс, шт	Ошибка, тыс. шт.
Январь - март 1996	1	239	+42,6	200	-3,6
Апрель – июнь	2	201	-20,7	220	+1,7
Июль – сентябрь	3	182	-62,0	240	+4,0
Октябрь – декабрь	4	297	+40,1	260	-3,1
Январь - март 1997	5	324	+42,6	280	+1,4
Апрель – июнь	6	278	-20,7	300	-1,3
Июль – сентябрь	7	257	-62,0	320	-1,0
Октябрь – декабрь	8	384	+40,1	340	+3,9
Январь - март 1998	9	401	+42,6	360	-1,6
Апрель – июнь	10	360	-20,7	380	+0,7
Июль – сентябрь	11	335	-62,0	400	-3,0
Октябрь – декабрь	12	462	+40,1	420	+1,9
Январь - март 1999	13	481	+42,6	440	-1,6

Как и в случае линейной регрессии для того, чтобы найти меру соответствия модели исходным данным, необходимо вычислить значения ошибок (остатков) модели, то есть той части значения наблюдения, которую невозможно объяснить с помощью построенной модели. Для этого применяют среднее абсолютное отклонение (mean absolute deviation - MAD) и среднеквадратическую ошибку (mean square error - MCE).

Целесообразно использовать обе меры, так как последняя их этих мер резко возрастает при наличии высоких ошибок.

Мы можем использовать в шаге 4 последний столбец таблицы 5 для расчета MAD и MSE.

;

В нашем случае ошибки достаточно малы и составляют от 1 до 3% от уровней ряда. Тенденция, выявленная по фактическим данным, достаточно устойчива и позволяет получить хорошие краткосрочные прогнозы.

Прогнозные значения по модели с аддитивной компонентой рассчитывают как:

F=T+S (тыс. шт. за квартал),

где трендовое значение Т=180+20номер квартала, а сезонная компонента S составляет +42,6 в январе-марте, -20,7 в апреле-июне, 62,0 в июле-сентябре и +40,1 в октябре-декабре.

Порядковый номер квартала, охватывающего ближайшие три месяца с апреля по июль 1999 г., равен 14, таким образом, прогнозное трендовое значение составит:

Т₁₄=180+2014=460 (тыс. шт. за квартал).

Соответствующая сезонная компонента равна –20,7 тыс. шт. Следовательно, прогноз на этот квартал определяется как:

F (апрель-июнь 1999г.)=460-20,7=439,3 тыс. шт.

Не следует забывать: чем более отдаленным является период упреждения, тем меньшей оказывается обоснованность прогноза. В данном случае мы предполагаем, что тенденция, обнаруженная по ретроспективным данным, распространяется и на будущий период. Для сравнительно небольших периодов упреждения такая предпосылка может действительно иметь место, однако ее выполнение становится менее вероятным по мере сопоставления прогнозов на более отдаленную перспективу.

Рассмотрим практическую реализацию методики решения задачи для модели с мультипликативной компонентной.

В некоторых временных рядах значение сезонной компоненты не является константой, а представляет собой определенную долю трендового значения. Таким образом, значения сезонной компоненты увеличиваются с возрастанием значений тренда.

Пример 2. Компания LORA Ltd осуществляет реализацию нескольких видов продукции. Объемы продаж одного из продуктов за последние 13 кварталов представлены в таблице 6.

Таблица 6. Квартальные объемы продаж компании LORA Ltd

Дата	Номер квартала	Количество проданной продукции, тыс. шт.
Январь-март 1996	1	70
Апрель-июнь	2	66
Июль-сентябрь	3	65
Октябрь-декабрь	4	71
Январь-март 1997	5	79
Апрель-июнь	6	66
Июль-сентябрь	7	67
Октябрь-декабрь	8	82
Январь-март 1998	9	84
Апрель-июнь	10	69
Июль-сентябрь	11	72
Октябрь-декабрь	12	87
Январь-март 1999	13	94

Построим график, позволяющий сделать выводы о типе модели:

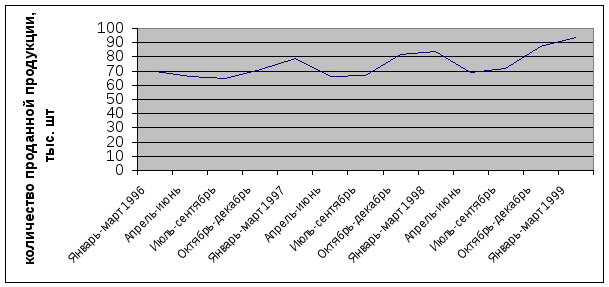
Объем продаж этого продукта так же, как и в предыдущем примере, подвержен сезонным колебаниям, и значения его в зимний период выше, чем в летний. Однако размах вариации фактических значений относительно линии тренда постоянно возрастает. К таким данным следует применять модель с мультипликативной компонентной:

Фактическое значение = Трендовое значение Сезонная вариацияОшибка,

т.е.

А = T S E

В нашем примере есть все основания предположить существование линейного тренда, но чтобы полностью в этом убедиться, проведем процедуру сглаживания временного ряда.

В сущности эта процедура ничем не отличается от той, которая применялась для аддитивной модели. Так же вычисляются центрированные скользящие средние для трендовых значений, однако оценки сезонной компоненты представляют собой коэффициенты, полученные по формуле А/Т= S E. Результаты расчетов приведены в табл. 7.

Таблица 7. Расчет значений сезонной компоненты для LORA Ltd

Дата	Номер квартала	Объем продаж, тыс. шт. А	Скользящая средняя за четыре квартала	Центриро-ванная скользящая средняя	Коэффициент сезонности А/Т= S E.
1	2	3	4	5	6
Январь-март 1996	1	70
Апрель-июнь	2	66	68
Июль-сентябрь	3	65	70,25	69,13	0,940
Октябрь-декабрь	4	71	70.25	70,25	1,011
Январь-март 1997	5	79	70,75	70,50	1,121
Апрель-июнь	6	66	73,50	72,13	0,915
Июль-сентябрь	7	67	74,75	74,13	0,904
Октябрь-декабрь	8	82	75,50	75,13	1,092
Январь-март 1998	9	84	76,75	76,13	1,103
Апрель-июнь	10	69	78	77,38	0,892
Июль-сентябрь	11	72	80,50	79,25	0,909
Октябрь-декабрь	12	87		-	-
Январь-март 1999	13	94		-	-

Значения сезонных коэффициентов получены на основе квартальных оценок по аналогии с алгоритмом, который применялся для аддитивной модели. Так как значения сезонной компоненты - это коэффициенты, а число сезонов равно четырем, необходимо, чтобы их сумма была равна четырем, а не нулю, как в предыдущем случае. (Если бы в исходных данных предполагалось семь сезонов в течение недели по одному дню каждый, то общая сумма значений сезонной компоненты должна была бы равняться семи). Если эта сумма не равна четырем, производится корректировка значений сезонной компоненты точно таким же образом, как это уже делалось ранее. В таблице оценки, рассчитанные в последнем столбце предшествующей табл. 8, расположены под соответствующим номером квартала.

Таблица 8.Расчет значений сезонной компоненты для LORA Ltd

	Год	Номер квартала
		1	2	3	4
	1996	-	-	0,940	1,011
	1997	1,121	0,915	0,904	1,092
	1998	1,103	0,892	0,909	-
Итого		2,224	1,807	2,77753	2,103
Среднее значение		2,2242	1,8072	2,7532	2,1032
Оценка сезонной компоненты		1,112	0,903	0,918	1,051	Сумма =3,984
Скорректированная сезонная компонента		1,116	0,907	0,922	1,055	Сумма =0

Как показывают оценки, в результате сезонных воздействий объемы продаж в январе-марте увеличиваются на 11,6 % соответствующего значения тренда (1,116). Аналогично сезонные воздействия в октябре-декабре приводят к увеличению объема продаж на 5,5 % от соответствующего значения тренда. В двух других кварталах сезонные воздействия состоят в снижении объемов продаж, которое составляет 90,7 и 92,2 % от соответствующих трендовых значений.

После того, как оценки сезонной компоненты определены, можем приступить к процедуре десезонализации по формуле А/S= T E. Результаты расчетов этих оценок значений тренда приведены в табл. 9.

Таблица 9. Расчет уравнения тренда для компании LORA Ltd

Дата	Номер квартала	Объем продаж, тыс. шт., А	Коэффициент сезонности, S	Десезонализированный объем продаж, тыс. шт. А/T= S E
Январь-март 1996	1	70	1,116	62,7
Апрель-июнь	2	66	0,907	72,8
Июль-сентябрь	3	65	0,922	70,6
Октябрь-декабрь	4	71	1,055	67,3
Январь-март 1997	5	79	1,116	70,8
Апрель-июнь	6	66	0,907	72,8
Июль-сентябрь	7	67	0,922	72,7
Октябрь-декабрь	8	82	1,055	77,7
Январь-март 1998	9	84	1,116	75,2
Апрель-июнь	10	69	0,907	76,1
Июль-сентябрь	11	72	0,922	78,2
Октябрь-декабрь	12	87	1,055	82,4
Январь-март 1999	13	94	1,116	84,2

Теперь нужно принять решение о том, какой вид будет иметь уравнение тренда. Очевидно, что линия тренда - не кривая, наоборот, она несколько больше напоминает прямую, хотя отдельные точки, особенно значения за 1996 г, расположены хаотически. Предположим для простоты, что тренд линейный, и для расчета параметров прямой, наилучшим образом его аппроксимирующей, будем применять метод наименьших квадратов, который дает следующий результат:

Т = 64,6 + 1,36 номер квартала (тыс. шт. в квартал).

Это уравнение будем использовать в дальнейшем для расчета оценок трендовых объемов продаж на каждый момент времени.

Итак, мы нашли значения тренда и сезонной компоненты. Теперь мы можем использовать их для того, чтобы рассчитать ошибки в прогнозируемых по модели объемах продаж ТS по сравнению с фактическими значениями А. В табл.10 эти ошибки рассчитаны как отношение Е = А/(Т S).

Для каждого года ошибки достаточно велики, что видно из графика десезонализированных значений. Однако, начиная и первого квартала 1997 г., величина ошибки составляет в среднем 2-3 % от фактического значения, и можно сделать вывод о соответствии построенной модели фактическим данным.

Таблица 10.Расчет ошибок для компоненты LORA Ltd.

Дата	Номер квар-тала	Объем продаж, тыс. шт. А	Сезонная компо-нента, S	Трендовое значение, тыс. шт., Т	Ошибка
					ТS	А/(ТS).	А-(ТS).
Январь-март 1996	1	70	1,116	66,0	73,7	0,95	-3,7
Апрель-июнь	2	66	0,907	67,3	61,0	1,08	+5,0
Июль-сентябрь	3	65	0,922	68,7	63,3	1,03	+1,7
Октябрь-декабрь	4	71	1,055	70,0	73,9	0,96	-2,9
Январь-март 1997	5	79	1,116	71,4	79,7	0,99	-0,7
Апрель-июнь	6	66	0,907	72,8	66,0	1,00	0
Июль-сентябрь	7	67	0,922	74,1	68,3	0,98	-1,3
Октябрь-декабрь	8	82	1,055	755,5	79,7	1,03	+2,3
Январь-март 1998	9	84	1,116	76,8	85,7	0,98	-1,7
Апрель-июнь	10	69	0,907	78,8	70,9	0,97	-1,9
Июль-сентябрь	11	72	0,922	79,6	73,3	0,98	-1,3
Октябрь-декабрь	12	87	1,055	80,9	85,4	1,02	+1,6
Январь-март 1999	13	94	1,116	82,3	91,9	1,02	+2,1

При составлении прогнозов по любой модели предполагается, что можно найти уравнение, удовлетворительно описывающее значение тренда. В обоих изложенных выше примерах эти предпосылка была успешно выполнена. Тренд, который нами рассматривался, был очевидно линейный. Если бы исследуемый тренд представлял собой кривую, мы были бы вынуждены моделировать эту связь с помощью одного из методов формализации нелинейных взаимосвязей, рассмотренных в предыдущей главе. После того, как параметры уравнения тренда определены, процедура составления прогнозов становится совершенно очевидной. Прогнозные значения определяются по формуле:

F= ТS,

где

Т=64,6+1,36номер квартала (тыс. шт. за квартал),

а сезонные компоненты составляют 1,116 в первом квартале, 1,097 - во втором, 0,922 - в третьем и 1,055 в четвертом квартале. Ближайший следующий квартал - это второй квартал 1999г., охватывающий период с апреля по июнь и имеющий во временном ряду порядковый номер 14. Прогноз объема продаж в этом квартале составляет:

F= Т S = (64 + 1,36 14)0,907 = 83,640,907 = 75,9 (тыс. шт. за квартал).

С учетом величины ошибки прогноза мы можем сделать вывод, что данная оценка будет отклоняться от фактического значения не более, чем на 2 - 3 %. Аналогично, прогноз на октябрь-декабрь 1999 г., рассчитывается для квартала с порядковым номером 16 с использованием значения сезонной компоненты для IV квартала года:

F = Т S = (64 + 1,36 16)1,055 = 83,361,055 = 91,1(тыс. шт. за квартал).

Разумно предположить, что величина ошибки данного прогноза будет несколько выше, чем предыдущего, поскольку этот прогноз рассчитан на более длительную перспективу.