4. Модели временных рядов

1. Основные понятия и показатели

Временные ряды (ряды динамики, хронологические ряды, Time Series) - это ряды чисел, показывающие изменение изучаемого явления во времени.

Временные ряды бывают интервальными и моментными.

В интервальных рядах приводятся уровни явления за последовательные интервалы времени.

Пример интервального ряда дается ниже.

Таблица 4.1. Добыча угля в Ростовской области, млн. т

Год	Добыча угля, млн. т
1995	19,4
1996	16,7
1997	14,1
1998	10,9
1999	10,1

В моментных рядах данные приводятся на последовательные моменты времени.

Пример моментного ряда:

Таблица 4.2. Численность наличного населения Ростовской области на начало года, тыс. чел.

Год	1996	1997	1998	1999	2000
Наличное население, тыс. чел.		4420,0	4403,9	4384,2	4357,9

К числу показателей, характеризующих временные ряды, относятся следующие:

- средний уровень ряда,

- абсолютные приросты (цепные и базисные),

- темпы (коэффициенты) роста (цепные и базисные),

- темпы (коэффициенты) прироста (цепные и базисные),

- абсолютное содержание одного процента прироста,

- средний абсолютный прирост,

- средний темп роста,

- средний темп прироста²и др.

2. Анализ и прогнозирование временных рядов

Уровни временного ряда формируются под влиянием действия множества факторов, часть из которых определяет основную тенденцию развития явления (тренд), а остальные – обусловливают колебания уровней ряда вокруг линии тренда. При этом колеблемость вокруг линии тренда также можно разложить на части: некую систематическую составляющую (например, сезонные колебания) и случайную колеблемость.

Таким образом, динамика уровней ряда включает три составляющих:

- основную тенденцию развития (тренд);

- систематическую колеблемость вокруг линии тренда;

- случайную (несистематическую) колеблемость вокруг линии тренда.

4.2.1. Анализ и прогнозирование временных рядов с трендом

К числу приемов выявления основной тенденции временных рядов можно отнести укрупнение интервалов, сглаживание и аналитическое выравнивание.

Укрупнение интервалов представляет собой замену данных, имеющих отношение к мелким временным периодам, данными по более крупным периодам. Например, можно заменить суточные данные недельными или декадными, декадные – месячными, месячные – квартальными и т.д.

Например, объем продажи валюты на биржах меняется изо дня в день под влиянием самых разнообразных факторов, включая и чисто случайные. Относительно меньшую колеблемость обнаруживают недельные объемы продажи валюты, еще меньшую - месячные и далее - квартальные. Объединив мелкие интервалы в крупные, мы погасим известную часть случайной колеблемости и получим возможность более отчетливо показать основную тенденцию развития событий на валютных биржах.

Недостатком этого приема является то, что с переходом к более крупным интервалам длина ряда сильно укорачивается. Поэтому, имея очень короткий ряд, выявить с его помощью какую-либо тенденцию развития невозможно. Таким образом, применение этого приема приходится ограничить лишь теми случаями, когда исходный временной ряд достаточно длинен.

Сглаживание временных рядов осуществляется с помощью скользящей средней. Эта средняя исчисляется для нескольких уровней, входящих в интервал сглаживания, и затем (при центрировании) относится к середине этого интервала.

Расчет скользящей средней по данным примера о динамике добычи угля в Ростовской области (таблица 4.1.) имеет следующий вид:

Таблица 4.3. Сглаживание ряда добычи угля в Ростовской области с помощью скользящей средней

Год	Добыча угля
	Фактические данные	Данные, сглаженные с помощью скользящей средней
1995	19,4	-
1996	16,7	(19,4+16,7+14,1):3 = 16,73
1997	14,1	(16,7+14,1+10,9):3 = 13,9
1998	10,9	(14,1+10,9+10,1):3 = 11,97
1999	10,1	-

В общем виде расчет скользящей средней для i-того периода можно записать так:

(4.1)

Эта формула верна для сглаживания по трем точкам.

Для для сглаживания по пяти точкам она примет следующий вид:

Сглаживание методом скользящей средней можно проводить по любому числу членов т, но удобнее, если т — нечетное число, так как в этом случае скользящая средняя сразу относится к конкретной временной точке — середине (центру) интервала. Если же т — четное, то скользящая средняя относится к промежутку между временными точками: например, при сглаживании по четырем членам средняя из первых четырех уровней будет находиться между второй и третьей датой, следующая средняя — между третьей и четвертой и т.д. Тогда, чтобы сглаженные уровни относились непосредственно к конкретным временным точкам (датам), из каждой пары смежных промежуточных значений скользящих средних находят среднюю арифметическую, которую и относят к определенной дате (периоду). Такой прием называется центрированием.

Недостатком метода скользящей средней является то, что сглаженный ряд «укорачивается» по сравнению с фактическим с двух концов: при нечетном т на (m - 1)/2 с каждого конца, а при четном — на т/2 с каждого конца.

Применяя этот метод, надо помнить, что он сглаживает (устраняет) лишь случайные колебания.

Если же, например, ряд содержит сезонную волну, она сохранится и после сглаживания методом скользящей средней.

Кроме того, этот метод сглаживания, как и укрупнение интервалов, является механическим, эмпирическим и не позволяет выразить общую тенденцию изменения уровней в виде математической модели.

Аналитическое выравнивание. Более совершенный метод обработки временных рядов в целях устранения случайных колебаний и выявления тренда — выравнивание уровней ряда по аналитическим формулам (аналитическое выравнивание). Суть аналитического выравнивания заключается в замене эмпирических (фактических) уровней y теоретическими , которые рассчитаны по определенному уравнению, принятому за математическую модель тренда, где теоретические уровни рассматриваются как функция времени: .

При этом каждый фактический уровень y рассматривается как сумма двух составляющих: , где — систематическая составляющая, отражающая тренд и выраженная определенным уравнением, а — случайная величина, вызывающая колебания уровней вокруг тренда.

Задача аналитического выравнивания сводится к следующему:

• определение на основе фактических данных вида (формы) гипотетической функции 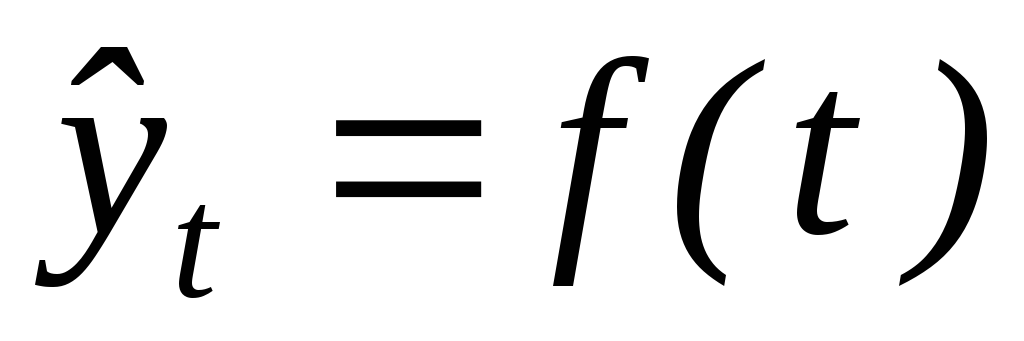, способной наиболее адекватно отразить тенденцию развития исследуемого показателя;

• нахождение по эмпирическим данным параметров указанной функции (уравнения);

• расчет по найденному уравнению теоретических (выравненных) уровней.

Наиболее простые модели аналитического выравнивания:

- линейная: ;

- показательная: ;

- экспоненциальная: ;

- гиперболическая: ;

- парабола 2-го порядка: и др.

Несложно заметить, что в качестве объясняющей переменной в трендовых уравнениях регрессии выступает фактор времени t.

Выбор аналитической функции для выравнивания временного ряда осуществляется, как правило, на основании графического изображения эмпирических данных, дополняемого содержательным анализом особенностей развития исследуемого показателя (явления). Вспомогательную роль при выборе аналитической функции играют механические приемы сглаживания (укрупнение интервалов и метод скользящей средней). Частично устраняя случайные колебания, они помогают более точно определить тренд и выбрать адекватную модель для аналитического выравнивания.

Существует ряд рекомендаций для выбора аналитической функции:

1. Выравнивание по прямой (линейной) функции эффективно для рядов, уровни которых изменяются примерно в арифметической прогрессии, т.е. когда первые разности уровней (абсолютные приросты) примерно постоянны.

2. Если примерно постоянны вторые разности уровней (ускорения), то такое развитие хорошо описывается параболой 2-го порядка . Если постоянны п-е разности уровней, можно использовать параболу п-го порядка , позволяющую «улавливать» перегибы, смену направлений изменения уровней. Парабола 2-го порядка отражает развитие с ускоренным или замедленным изменением уровней ряда.

3. Если при последовательном расположении t (меняющемся в арифметической прогрессии) значения уровней меняются в геометрической прогрессии, т.е. цепные коэффициенты роста примерно постоянны, то такое развитие можно отразить показательной или экспоненциальной функцией.

4. Если обнаружено замедленное снижение уровней ряда, которые по логике не могут снизиться до нуля, для описания характера тренда выбирают гиперболу и т.д.

Рассмотрим выбор формы уравнения тренда на следующем примере:

Таблица 4.4. Динамика среднегодовой численности промышленно-производственного персонала в промышленности в Ростовской области (тыс.чел.)

Годы	Среднегодовая численность промышленно-производственного персонала в промышленности
1993	569,7
1994	516,4
1995	472,0
1996	431,0
1997	395,8
1998	365,1

Расчитаем первые и вторые разности, а также коэффициенты роста.

	yt
1993	569,7
1994	516,4	-53,3		0,906
1995	472,0	-44,4	8,9	0,914
1996	431,0	-41,0	3,4	0,913
1997	395,8	-35,2	5,8	0,918
1998	365,1	-30,7	4,5	0,922

Наибольшей стабильностью отличаются коэффициенты роста, поэтому, видимо, для описания тренда следует выбрать либо показательную, либо экспоненциальную функцию.

К аналогичным выводам можно прийти, анализируя график динамики среднегодовой численности ППП в Ростовской области (рис. 12).

Судя по графику динамики среднегодовой численности ППП в Ростовской области, для прогноза лучше всего использовать показательную, экпоненциальную либо линейную функцию.

Рис.12. Динамика среднегодовой численности ППП в Ростовской области

Несмотря на эти выводы, рассмотрим механизм расчета параметров всех вышеперечисленных моделей.

Параметры искомых уравнений при аналитическом выравнивании могут быть определены различными способами. Чаще всего для этого используется метод наименьших квадратов.

В частности для нахождения параметров уравнения прямойможет быть использован следующий алгоритм:

(4.2)

Если периоды или моменты времени пронумеровать так, чтобы получилось , то вышеприведенные алгоритмы существенно упростятся и примут следующий вид:

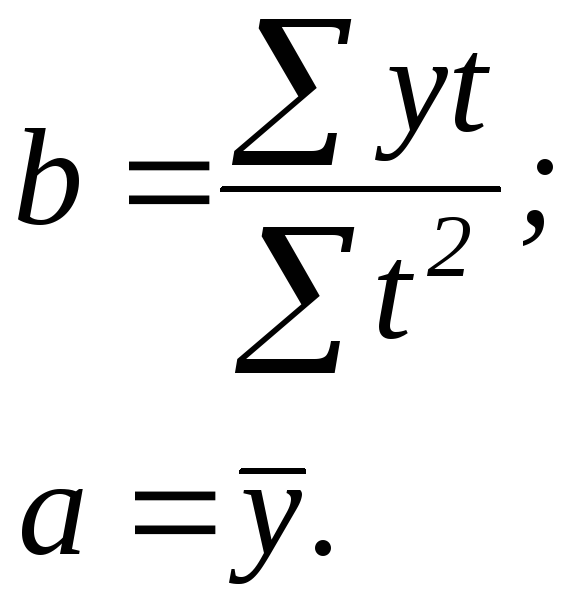(4.3)

В нашем примере – 6 уровней ряда. Для того, чтобы сумма порядковых номеров уровней ряда была равна нулю, нулевым моментом следует принять промежуток между 1995 и 1996 гг. Тогда порядковый номер 1993 года будет равен -2,5, 1994 - -1,5 и т.д. Их сумма равна нулю, что в дальнейшем упростит расчеты. Для их осуществления составим рабочую таблицу 4.5:

Таблица 4.5.

Годы	T	y	Yt	t2
1993	-2,5	569,7	-1424,25	6,25
1994	-1,5	516,4	-774,6	2,25
1995	-0,5	472,0	-236	0,25
1996	0,5	431,0	215,5	0,25
1997	1,5	395,8	593,7	2,25
1998	2,5	365,1	912,75	6,25
Суммы	0	2750	-712,9	17,5

Отсюда:

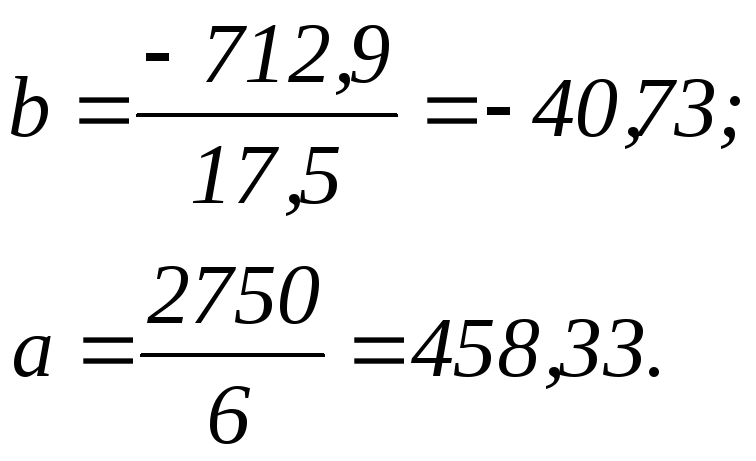
При таких параметрах уравнение получит следующий вид:

Дадим интерпретацию параметров тренда.

Коэффициент регрессии (b) в линейном тренде показывает средний за период цепной абсолютный прирост уровней ряда. В нашем примере b = -40,73, следовательно среднегодовая численность ППП в среднем за год снижается на 40,73 тыс.чел. Свободный член (а) в линейном тренде выражает начальный уровень ряда в момент (период времени) t = 0. В нашей нумерации t = 0 приходится на период времени между 1996 и 1997 гг., что несколько затрудняет его интерпретацию. В нашем случае а = 458,33 тыс.чел. – это средняя численность ППП за вторую половину 1996 и первую половину 1997 гг.

С помощью этого уравнения найдем выравненные уровни и рассчитаем стандартную ошибку уравнения регрессии S_yx.

.

Расчеты проведем в рабочей таблице 4.6:

Таблица 4.6.

	T
1994	-2,5	569,7	560,1762	9,5238	90,7029
1995	-1,5	516,4	519,4390	-3,0390	9,2358
1996	-0,5	472,0	478,7019	-6,7019	44,9155
1997	0,5	431,0	437,9648	-6,9648	48,5079
1998	1,5	395,8	397,2276	-1,4276	2,0381
1999	2,5	365,1	356,4905	8,6095	74,1239
Суммы	0	2750	2750	0	269,5242

Чем меньше стандартная ошибка, тем лучше подобрана модель тренда. Сравнение S_{yx ,} рассчитанных для различных моделей дает возможность выбрать лучшую из них.

Рассмотрим использование для аналитического выравнивания других (нелинейных) моделей.

Для определения параметров нелинейных уравнений регрессии необходимо привести их к линейному виду. Рассмотрим алгоритмы линеаризации некоторыхиз них.

Уравнение гиперболы: .

Чтобы привести к линейному виду уравнение гиперболы, необходимо ввести переменную . Тогда уравнение примет линейный вид: и его параметры можно рассчитывать обычным МНК.

Расчет по данным нашего примера даст следующие результаты (при условии, что ):

b= -26,5222;a= 458,3333;S_yx= 75,5534.

При таких параметрах уравнение получит следующий вид:

.

Учитывая, что S_yx– намного больше, чем в уравнении прямой, можно сделать вывод, модель гиперболы хуже описывает динамику численности ППП в Ростовской области.

Уравнение параболы: .

Аналогичный прием используется и при определении параметров уравнения параболы. Приняв , получим: - линейное уравнение множественной регрессии.

Расчет по данным нашего примера даст следующие результаты (при условии, что ):

b₁= -40,7371;b₂= 2,6750;a= 450,5313;S_yx= 0,8909.

При таких параметрах уравнение получит следующий вид:

.

Как мы видим, в данном случае S_yx– меньше, чем в уравнении прямой, т.е. парабола 2-го порядка лучше других моделей описывает динамику численности ППП в Ростовской области.

Показательная функция: .

Линеаризация показательной функции достигается путем ее логарифмирования:

.

Это – линейное уравнение. Правда, при определении его параметров мы получим десятичные логарифмы aиb.

Расчет по данным нашего примера даст следующие результаты (при условии, что ):

lgb= -0,0386;lga= 2,6562;S_yx= 2,7977.

При таких параметрах уравнение получит следующий вид:

.

Найдем aиb.

b = 10^-0,0386 = 0,915.

Данная величина является среднегодовым коэффициентом роста. В нашем примере его величина указывает на то, что среднегодовая численность ППП в Ростовской области снижалась на 8,5 % в среднем за год.

a = 10^2,6562 = 453,1062.

Таким образом, искомое уравнение будет иметь такой вид:

.

Судя по величине стандартной ошибки S_yx= 2,7977, показательная функция лучше, чем линейная, но хуже, чем параболическая описывает динамику ППП в Ростовской области.

Экспоненциальная функция: .

В данным случае для линеаризации лучше использовать натуральные логарифмы:

.

Снова имеем линейное уравнение.

Расчет по данным нашего примера даст следующие результаты (при условии, что ):

b= -0,089;lna= 6,116;S_yx= 2,7573.

При таких параметрах уравнение получит следующий вид:

.

Найдем a:

a = e^6,116 = 453,0489.

b = -0,089. Данная величина является среднегодовым коэффициентом прироста. В нашем примере его величина указывает на то, что среднегодовая численность ППП в Ростовской области снижалась на 8,9 % в среднем за год.

Таким образом, искомое уравнение будет иметь такой вид:

.

Судя по величине стандартной ошибки S_yx= 2,7573, экспоненциальная функция лучше, чем линейная, но хуже, чем параболическая описывает динамику ППП в Ростовской области.

Разумеется, решение относительно функциональной формы уравнения тренда принимаются, не только исходя из величины стандартной ощибки уравнения тренда. Необходимо, принимать во внимание цели аналитического выравнивания, оценивать значимость уравнения регрессии в целом, а также его параметров.

Так, в нашем примере наименьшую стандартную ошибку имеет уравнени параболы. Однако его лучше всего использовать для интерполяции (расчета промежуточных значений). Очевидно, что прогноз (экстраполяцию) с помощью уравнения параболы делать нельзя.

Так как наименьшую и примерно одинаковую стандартную ошибку имеют показательная и экспоненциальная функции, для прогнозирования, видимо, лучше использовать одну из них.

Таким образом, мы пришли к тем же выводам, что и в начале анализа данного временного ряда.

Несмотря на все вышеприведенные соображения, необходимо проверять значимость трендового уравнения регрессии. Алгоритм проверки ничем не отличается от проверки значимости любого другого уравненния регрессии.

В качестве критерия проверки статистической гипотезы о значимости уравнения регрессии используется критерий F– Фишера-Снедекора.

Несложно убедиться в том, что в нашем примере на уровне значимости α = 0,05 можно доверять всем уравнениям за исключением уравнения гиперболы.

Прогнозирование временных рядов с трендом.

Если не учитывать систематическую колеблемость вокруг линии тренда (например, сезонную колеблемость), то прогнозирование сводится к подстановке в уравнения регрессии значений t, относящихся к соответствующему периоду упреждения.

Прогноз бывает точечным и интервальным.

Точечный прогноз по уравнению тренда - это расчетное значение переменной y, полученное путем подстановки в уравнение тренда соответствующих значений t.

По сравнению с точечным значительно большую практическую ценность имеет интервальный прогноз, позволяющий с заданной надежностью (доверительной вероятностью) γопределить границы интервала, в которых будет находиться уровень изучаемого призака в прогнозируемый период времени. Надежность точечного прогноза равна нулю.

Интервальный прогноз определяется двойным неравенством:

, (4.6)

где -прогноз значения переменнойy на момент (период) времени t;

- точечная оценка значения переменной y на момент (период) времени t;

- предельная ошибка прогноза.

Предельная ошибка прогноза рассчитывается по формуле:

, (4.7)

где - табличное значение t - критерия Стьюдента для уровня значимости α = 1 - γ и числа степеней свободы (k = n - 2);

- стандартная ошибка точечного прогноза, которая, в свою очередь, рассчитывается по формуле:

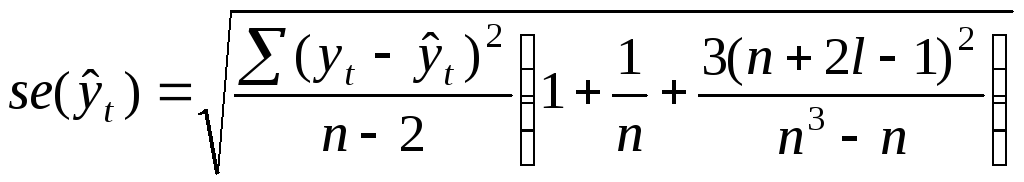, (4.8)

где - длина периода упреждения (срок прогноза).

Рассмотрим использование для прогнозирования линейного уравнения регрессии в примере о динамике среднегодовой численности ППП в Ростовской области.

Дадим точечный и интервальный прогноз численности ППП на 1999 год.

В нашей нумерации 1999 год соответствует моменту времени t = 3,5. Линейное уравнение динамики среднегодовой численности ППП в Ростовской области имеет вид:

Отсюда,

Следовательно, точечный прогноз среднегодовой численности ППП в Ростовской области на 1999 год составляет 315,75 тыс.чел.

Определим границы доверительного интервала, в котором с заданной надежностью γ будет находится среднегодовая численности ППП в Ростовской области в 1999 году.

Общепринятый в экономике уровень надежности γ = 1 - α = 1 - 0,05 = 0,95.

Найдем стандартную ошибку прогноза:

.

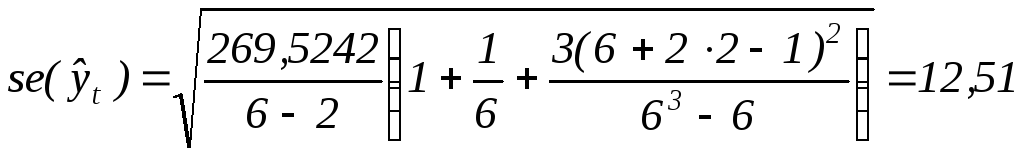Табличное значение t - критерия Стьюдента для уровня значимости α = 0,05 и числа степеней свободы k = 6 – 2 = 4 составляет 2,78, т.е. =2,78.

Отсюда,

Таким образом,

;

.

С вероятностью 0,95 можно ожидать, что в 1999 году среднегодовая численность ППП в Ростовской области будут находиться в пределах от 280,96 до 350,54 тыс. чел.

Обратите внимание на то, что приведенные формулы верны только для уравнения парной регрессии, линейной по параметрам.