Матрицы. Основные понятия.
Линейные операции над матрицами и их свойства.
Матрицей называется прямоугольная таблица состоящая
из m-строк и n- столбцов
Матрица, у которой число строк и столбцов равно – называется
квадратной.
Матрица, все элементы которой, кроме элементов главной диагонали
равны нулю,называется диагональной.
Диагональная матрица, у которой все элементы главной диагонали равны 1,
называется единичной..
Матрица, у которой все элементы равны 0, называется нулевой
2.Определитель матрицы. Свойства определителей.
1 Величина определителя не изменится, если его строки заменить
столбцами с теми же номерами.
2 Если поменять местами два столбца или две строки знак изменится
на противоположный.
3 Если определитель содержит два одинаковых столбца или две
одинаковые строки, он равен нулю.
4 Если все элементы одного из рядов определителя равны 0,то
и определитель равен нулю
5 Общий множитель элементов строки или столбца, можн вынести
за знак определителя.
6 Величин опеделителя=сумме произведеня элементов произвольно
выбраной строки или столбца.
7. Если В получена из А прибавлением к некоторому ряду
другого ряда умноженного на , то detA=detВ.
8Если в О каждый элемент некоторого ряда равен сумме 2 слагаем.,
то О равен сумме двух О. у одного стоят первые, а у второго вторые слагаемые.
3.Миноры и алгебраические дополнения.
Минором элемента матрицы n-го порядка называется определитель матрицы
полученный из матрицы
А вычеркиванием i-й строки и j-го столбца.
Алгебраическим дополнением Аij элемента аij матрицы n-го порядка называется
его минор, взятый со знаком,
зависящий от номера строки и номера столбца:
6.Некоторые методы вычисления определителей.
Теорема (Лапласа) Определитель матрицы порядка N = сумме
произведения всех миноров k-го порядка которые можно составить
из произвольно выбранных k паралельных рядов и алгебраичекских
дополнений этих миноров
Теорема (о разложении определителя по элементам ряда)
Определитель кв. матрицы=сумме
произведений элементов некоторого ряда и и алгебрраических
дополнений этих элементов
7.Умножение матриц. Свойства умножения.
Операция умножения возможна, если количество столбцов первой матрицы равно
количеству строк другой матрицы.
1.
2.
3.
4.
8.Транспонирование матриц.
Матрица, полученная заменой каждой ее строки столбцом с тем же номером,
называется матрицей транспонированной, к данной.
1.
2.
9.Обратная матрица. Необходимое и достаточное
условие существования обратной матрицы.
Нахождение обратной матрицы.
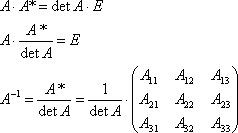
Для того чтобы матрица имела обратную достаточно того, чтобы она была
невырождена.
10.Матричная запись системы линейных уравнений и ее решение.
X=A(-1)B
A(-1) –матрица ,обратная к матрице А
11.Решение невырожденных систем. Формулы Крамера
Основная М является квадр. порядка n. если О этой М отличен
от 0, то система невырожденная.
Тогда М(А) - невырожденная, знач. имеет обратную. АХ=В,
А-1АХ= А-1В, Х= А-1В – формула решения системы в
матричной форме. Перепишем: Каждый элемент М стоящей справа
представляет собой произведен. чисел b1, … на
алгебр.допол. элементов первого и так далее ряда. Согласно теореме замещения:
b1A11+b2A21+…+bnAn1= =1
Аналогично 2,3,… Получаем х1=1/, х2=2/, …
хi=i/ i = (1,n) – формулы Крамера.
12.Ранг матрицы. Свойства ранга матрицы.
Вычисление ранга матрицы с помощью
элементарных преобразований.
Ранг – наибольший из порядков ее миноров, отличных от нуля.
Если все миноры = 0, то ранг = 0.
Способ: 1).все миноры 1-го порядка = 0, то r = 0;
2.)если один отличен от 0, а все 2-го = 0, то r =1;
3). К= 0 или их нет, то r = К-1.
Элементарные преобразования: 1) умножение некоторого ряда на
число отличное от 0;
2.) прибавление к одному ряду другого ему, умноженному на
произвольное число;
3.) перестановка местами двух рядов.