§ 11. Показательное (экпоненциальное) распределение
Определение.
Показательным
(экпоненциальным)
называется распределение СВ, имеющее
плотность
.
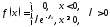+ График.
Функция
распределения в этом случае
.+
График.
Числовые характеристики показательного распределения.
Непосредственным
вычислением легко установить, что
,
.
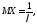
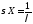Вероятность попадания в интервал.
.
Замечание. Показательное распределение является единственным непрерывным распределением, обладающим свойством «отсутствия последействия»:
,
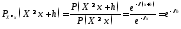т.е.
информация о том, что событие не наступило
к данному моменту, не улучшает шансы на
его наступление в дальнейшем. И для
любых
.
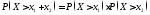Это свойство играет важную роль в задачах
теории массового обслуживания.
§ 12. Закон больших чисел
Закон больших чисел (ЗБЧ)– это общий принцип, в силу которого совместное действие случайных факторов приводит при некоторых весьма общих условиях к результату, почти не зависящему от случая. Сближение частоты наступления случайного события с его вероятностью при возрастании числа испытаний (подмеченное сначала, пожалуй, на азартных играх) может служить первым примером проявления этого принципа.
В узком смысле под ЗБЧ понимается ряд теорем, которые утверждают приближение средних характеристик большого числа опытов к некоторым постоянным величинам. В широком смысле этот закон утверждает, что при очень большом числе случайных явлений средний их результат перестает быть случайным и может быть предсказан с большой степенью определенности.
Определение.
Пусть
п
– число фактически проведенных опытов,
т
– количество испытаний, в которых
появилось событие А.
Тогда
называетсяотносительной
частотой события А.
Пример.
В XVIII
веке Жорж Бюффон провел опыт: он бросил
монету 4040 раз. При этом герб выпал 2048
раз. В начале ХХ века аналогичный опыт
поставил Карл Пирсон. Монета была брошена
1000 раз, и герб выпал 4979 раз. Как видим, в
этих опытах относительная частота
выпадения герба приближенно совпала с
вероятностью этого события:
.
Теорема 3. (Теорема Я.Бернулли) (1713 г.)
Пусть
производится п
независимых испытаний, в каждом из
которых вероятность наступления
некоторого случайного события А
имеет одно и то же значение р
;
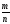– относительная частота наступления
этого события в той же серии испытаний.
Тогда для любого числа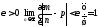
.
Теорема 4. (Теорема П.Л.Чебышёва) (1867 г.)
Пусть:
1)
− независимые случайные величины;
2)
их дисперсии ограничены одной и той же
константой
.
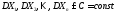Тогда
для любого числа
.
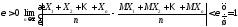Замечание 1. А.А.Марков (ученик П.Л.Чебышёва) доказал справедливость теоремы Чебышёва и для зависимых СВ. Суть этой теоремы состоит в том, что среднее арифметическое большого числа СВ утрачивает характер случайной величины.
Следствие.
Если
,
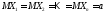то для любого числа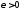
.
Замечание 2. Теорема Бернулли является следствием теоремы Чебышёва.
Некоторые применения теоремы Чебышёва и закона больших чисел:
1) для увеличения точности измерения физической величины увеличивают количество измерений. Но бесконечно увеличивать точность таким образом нельзя из-за ограниченности точности измерительных инструментов;
2) принцип диверсификации (разнообразия) работы банка. Он означает, что надо проводить разнообразные, не связанные друг с другом операции. Тогда убытки от одних операций будут более или менее покрыты прибылью от других операций;
3) для обеспечения репрезентативности выборки ее элементы должны отбираться случайным образом.