§ 9. Равномерное распределение

Определение. Пусть СВ Х принимает значения на отрезке .Равномерным называется распределение вероятностей СВ Х, заданное плотностью

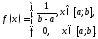
Равномерное распределение соответствует представлению о выборе точки из отрезка 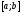«наудачу». Примером СВ, имеющей такое распределение, может быть величина погрешности измерения при округлении показаний прибора до ближайшего целого значения.

Числовые характеристики равномерного распределения вычисляются легко:

.

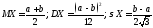Вероятность попадания значений СВ в отрезок .

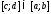
§ 10. Нормальное распределение

Определение. НСВ Х называется распределенной по нормальному закону, если плотность ее распределения имеет вид: 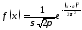, где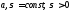. Числаа и называютсяпараметрами распределения.

Пример. Если производится измерение некоторой физической величины без систематических ошибок (взвешивание, измерение длины, измерение отклонения от идеального размера и т.д.) и на результат влияют многие независимые факторы (температура, влажность, колебания прибора и т.п.), то ошибка измерения имеет распределение, близкое к нормальному.

Вероятностный смысл параметров нормального распределения.

Непосредственными вычислениями можно установить, что для СВ Х, распределенной по нормальному закону, МХ=а, ,.

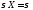Определение. Нормальное распределение с параметрами называетсянормированным.

+ График :,;

, ;

.

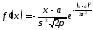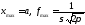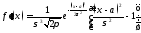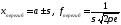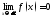Вероятность попадания в интервал.

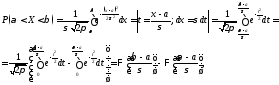
где 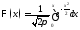− функция Лапласа (см. § 11, ч. 1) (ее значения можно найти в справочнике).

Вероятность заданного отклонения:

.

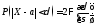Пример. СВ Х распределена по нормальному закону с параметрами . Найти вероятность того, чтоХ примет значение в интервале (12; 14).

Решение.

.

Правило «трёх сигм»

Уже знаем, что 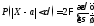. Обозначим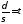. Получим

.

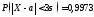При , следовательно,, а тогда, т.е. очень мала.

Отсюда получаем правило: для нормально распределенной СВ Х модуль ее отклонения от математического ожидания практически не превосходит .

Суть Центральной предельной теоремы Ляпунова: если СВ Х представляет собой сумму большого числа независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то Х имеет распределение, близкое к нормальному.

Для характеризации меры отклонения теоретического распределения 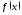от нормального используются величины, называемыеасимметрия и эксцесс.

Предположим, что у теоретического распределения и нормального распределения совпадают математические ожиданияМХ и дисперсии DX.

Асимметрия.

Напомним, что центральным моментом порядка k СВ Х называется 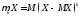. Если график плотности распределения симметричен относительно прямой, то все центральные моменты нечетных порядков равны нулю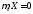. Нодля любой СВ. Поэтому для характеризации несимметричности плотности можно использовать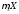. Поскольку значение этой величины зависит от единиц измерения СВХ, то асимметрией называют

.

При положительной (отрицательной) асимметрии более «длинная» часть графика плотности распределения лежит правее (левее) прямой 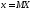. + Иллюстрация.

Эксцесс.

Эксцессом называют величину, вычисляемую по формуле

.

Он является характеристикой островершинности графика плотности распределения. Для нормального распределения 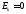. При положительном значении эксцесса график плотности распределения является более «энергичным», а при отрицательном – более пологим в сравнении с нормальной кривой. + Иллюстрация.

Распределение («хи-квадрат»)

Пусть – независимые нормально распределенные величины, имеющие параметры распределения. Тогда СВ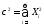имеетраспределение по закону 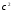сk=n степенями свободы.

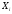
Если СВ были связаны между собойs различными условиями, то число степеней свободы распределения 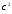будет равно .

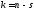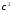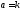Распределение определяется параметромk. С увеличением k распределение медленно приближается к нормальному. При большихk СВ будет иметь асимптотически нормальное распределение с параметрамии.