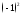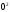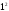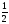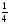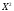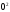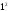2. Дисперсия

В предыдущем примере видим, что, хотя математические ожидания двух СВ совпадают, но значения этих величин имеют различный разброс вокруг своего математического ожидания. Как охарактеризовать величину этого разброса?

Первое, что приходит на ум, − рассмотреть математическое ожидание отклонения значений СВ от среднего. Рассмотрим произвольную СВ Х. Найдем :

.

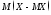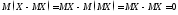Т.е. для любой СВ =0 и, следовательно, не годится для оценки величины разброса. Для этой цели подойдет следующая характеристика СВ.

Определение. Дисперсией СВ Х называется число (математическое ожидание квадрата отклонения значений случайной величины от ее математического ожидания).

Содержательный смысл дисперсии СВ состоит в том, что эта характеристика является мерой рассеяния значений СВ вокруг ее математического ожидания.

Замечание. Дисперсия случайной величины не является случайной величиной.

Пример. Найдем дисперсию числа гербов, выпавших при двух бросаниях монеты. В § 2 был составлен закон распределения этой СВ, а в п.1 текущего параграфа мы вычислили ее математическое ожидание: МХ=1. Составим закон распределения СВ :

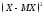Р

Вычислим дисперсию:

.

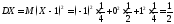Формула для вычисления дисперсии:

.

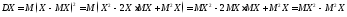Пример. Найдем с помощью этой формулы числа гербов, выпавших при двух бросаниях монеты. Составим закон распределения СВ :

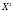Р

;

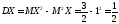, как и при вычислении дисперсии по определению.

Определение. Величина 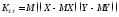называетсякорреляционным моментом СВ Х и Y.

Если СВ Х и Y независимы, то и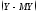тоже независимы и, следовательно,

,

т.е. 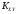характеризует наличие связи между СВ Х и Y.

Свойства дисперсии:

1) ;

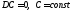2) ;

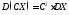3) 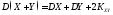, а для независимых СВ Х и Y ;

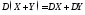4) ;

5) 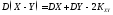, а для независимых СВ Х и Y .

3. Среднее квадратическое отклонение

Неудобство при использовании дисперсии для оценивания рассеивания СВ состоит в том, что единицы измерения дисперсии являются квадратами единиц измерения самой случайной величины. Следующая характеристика СВ свободна от этого недостатка.

Определение. Число 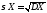называетсясредним квадратическим отклонением случайной величины Х.

Пример. Среднее квадратическое отклонение числа гербов, выпавших при двух бросаниях монеты, равно .

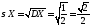Свойство среднего квадратического отклонения: для независимых СВ

.

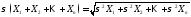4. Другие числовые характеристики

Определение. Начальным моментом порядка k СВ Х называется .

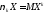Таким образом, Тогда.

Определение. Центральным моментом порядка k СВ Х называется .

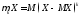Легко заметить, что .

§ 4. Биномиальное распределение. Распределение Пуассона

Определение. Биномиальным называется распределение дискретной СВ Х, которая принимает значения с вероятностями, вычисляемыми по формуле Бернулли:

.

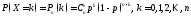По биномиальному закону распределено, например: а) число выпадений герба при двух бросаниях монеты; б) количество выпавших «пятерок» при 4 бросаниях кубика; в) количество взошедших семян (см. задачу 2 § 11, ч. 1).

Теорема 1. (О числовых характеристиках биномиального распределения)

Если СВ Х имеет биномиальное распределение с параметрами п, р и 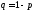, то,.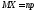

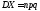Пример. а) Для СВ Х, равной числу выпадений герба при двух бросаниях монеты, ,,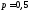. Тогда;;.

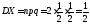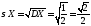б) Пусть СВ Х − количество выпавших «пятерок» при 4 бросаниях кубика. Тогда 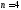,,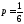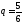. Следовательно,;;.

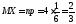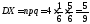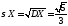в) Рассмотрим СВ Х, равную количеству взошедших семян из 400 посеянных при всхожести с вероятностью 0,8. Параметры схемы Бернулли в этом случае имеют значения ,,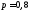. Тогда;;.

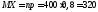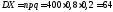Определение. Распределение дискретной СВ Х, которая принимает значения 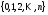с вероятностями, вычисляемыми по формуле Пуассона:

,

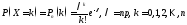называется распределением Пуассона.

При распределении Пуассона .

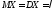Пример. Пусть СВ Х – число разбитых при транспортировке ламп из 1000, полученных депо, если вероятность разбиться для каждой лампы равна 0,003 (см. задачу 3 § 11, ч. 1). В этом случае п=1000, р=0,003, 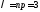. Следовательно,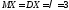.