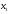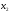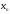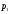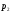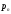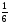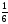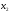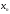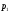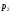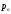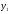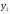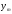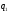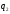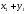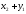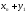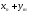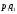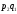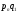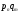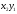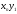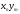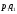Часть 2. Случайные величины

§ 1. Понятие случайной величины

Величины могут быть детерминированными или случайными. Детерминированная величина принимает определенные, заранее известные значения. Значения случайной величины можно определить только с некоторой вероятностью.

Пусть 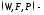вероятностное пространство. Если некоторая числовая величина принимает значения в зависимости от исхода случайного эксперимента, то такую величину естественно назватьслучайной. Таким образом. Случайная величина Х – это числовая функция, заданная на множестве 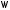. Случайные величины делятся на дискретные (прерывные) и непрерывные.

Случайная величина Х считается заданной, если для любого подмножества В множества действительных чисел R известна вероятность попадания значений Х в В: 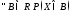известна. Заданная таким образом вероятность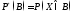называетсяраспределением случайной величины Х.

Примеры случайных величин:

1) число очков, выпавшее на кубике при одном бросании;

2) число гербов, выпавших при двух бросаниях монеты;

3) точность обработки детали;

4) абсцисса точки, брошенной на отрезок .

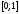Случайные величины в первых двух примерах являются дискретными, остальные – непрерывными.

§ 2. Дискретная случайная величина

Определение. Распределение случайной величины называется дискретным, если существуют числа 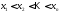такие, что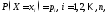и.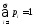

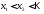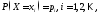Замечание. Дискретная случайная величина (ДСВ) может принимать счетное (бесконечное) число значений. В этом случае существуют числа , такие, чтои.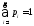

Определение. Законом распределения ДСВ называется таблица

Х			…
Р			…

Пример. 1) Закон распределения числа очков, выпавшего на кубике при одном бросании:

Х	1	2	…	6
Р			…

2) Закон распределения числа гербов, выпавших при двух бросаниях монеты:

Х	0	1	2
Р

Определение. Нанесем на плоскость в декартовой прямоугольной системе координат точки с координатами 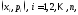и соединим их последовательно в порядке возрастания значений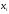. Полученная фигура называетсямногоугольником распределения.

§ 3. Числовые характеристики дискретной случайной величины

1. Математическое ожидание

Определение. Математическим ожиданием ДСВ называется число .

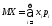Замечание. Математическое ожидание случайной величины не является случайной величиной, т.е. это величина детерминированная.

Пример. 1) Математическое ожидание числа очков, выпавшего на кубике при одном бросании, .

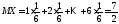2) Математическое ожидание числа гербов, выпавших при двух бросаниях монеты, .

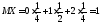Вероятностный смысл математического ожидания: среднее арифметическое значений, принятых случайной величиной в длинной серии опытов, приближенно равно ее математическому ожиданию.

Рассмотрим две ДСВ, заданных своими законами распределения:

Х			…
Р			…

Y			…
P			…

Определение. Суммой случайных величин Х и Y называется СВ X+Y, имеющая следующий закон распределения:

Х+Y			…		…
Р			…

Определение. Произведением случайных величин Х и Y называется СВ X·Y, имеющая следующий закон распределения:

Х·Y			…		…
Р			…

Определение. Случайные величины Х и Y называются независимыми, если

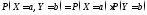для любых .

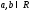Иными словами, закон распределения одной из этих СВ не зависит от того, какое значение приняла другая.

Свойства математического ожидания:

1) ;

2) ;

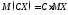3) ;

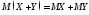4) для независимых СВ Х и Y .

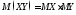Замечание. Математическое ожидание описывает СВ не полностью.

Пример. Рассмотрим две СВ:

Х	−100	100
Р	0,5	0,5

Y	−0,1	0,1
P	0,5	0,5

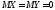, но очевидно, что СВ Х и Y различны.