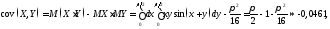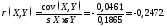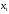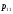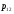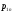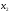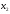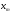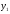§ 13. Двумерные случайные величины

Определение. Если на одном и том же пространстве элементарных событий заданы две случайные величиныХ и Y, то говорят, что задана двумерная случайная величина (Х,Y).

Пример. Станок штампует стальные плитки. Контролируются длина Х и ширина Y. − двумерная СВ.

СВ Х и Y имеют свои функции распределения и прочие характеристики.

Определение. Функцией распределения двумерной случайной величины (Х,Y) называется функция .

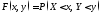Определение. Законом распределения дискретной двумерной случайной величины (Х,Y) называется таблица

			…
…

Здесь ;.

Для двумерной дискретной СВ .

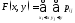Свойства :

1) ;

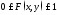2) если 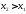, то; если, то;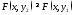

3) ;

;

4) − функция распределенияХ;

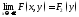−функция распределения Y.

Вероятность попадания значений двумерной СВ в прямоугольник:

Определение. Двумерная случайная величина (Х,Y) называется непрерывной, если ее функция распределения непрерывна наи имеет всюду ( за исключением, быть может, конечного числа кривых) непрерывную смешанную частную производную 2-го порядка.

Определение. Плотностью совместного распределения вероятностей двумерной непрерывной СВ называется функция .

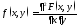Тогда, очевидно, .

Пример 1. Двумерная непрерывная СВ задана функцией распределения

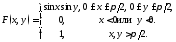
Тогда плотность распределения имеет вид

Пример 2. Двумерная непрерывная СВ задана плотностью распределения

.

Найдем ее функцию распределения:

.

Свойства :

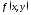1) ;

2) ;

3) для любой области .

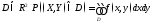Пусть известна плотность совместного распределения 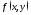. Тогда плотность распределения каждой из составляющих двумерной СВ находится следующим образом:

.

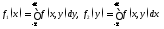Пример 2 (продолжение).

.

Плотности распределения составляющий двумерной СВ некоторые авторы называют маргинальными плотностями распределения вероятностей.

Условные законы распределения составляющих системы дискретных СВ.

Условная вероятность , где.

Условный закон распределения составляющей Х при :

Х			…
Р			…

Аналогично для , где.

Y			…
Р			…

Пример 3. Двумерная ДСВ задана законом распределения:

Х, Y	2	3
-1	0,10	0,06
1	0,30	0,18
2	0,20	0,16

Составим условный закон распределения Х при Y=2.

.

Тогда условный закон распределения

Х	-1	1	2
Р

Определение. Условной плотностью распределения составляющей Х при заданном значении Y=y называется .

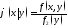Аналогично: .

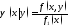Определение. Условным математическим ожиданием дискретной СВ Y при называется, где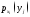− см. выше.

Следовательно, .

Для непрерывной СВ Y .

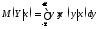Очевидно, что является функцией аргументах. Эта функция называется функцией регрессии Y на Х.

Аналогично определяется функция регрессии Х на Y: .

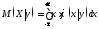Теорема 5. (О функции распределения независимых СВ)

СВ Х и Y являются независимыми тогда и только тогда, когда .

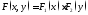Следствие. Непрерывные СВ Х и Y являются независимыми тогда и только тогда, когда .

В примере 1 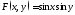при. Следовательно, СВХ и Y независимые.

Числовые характеристики составляющих двумерной случайной величины

Для дискретной СВ:

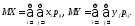
Для непрерывной СВ: .

Дисперсия и среднее квадратическое отклонение для всех СВ определяются по одним и тем же известным нам формулам:

.

Определение. Точка 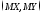называетсяцентром рассеивания двумерной СВ .

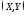Определение. Ковариацией (корреляционным моментом) СВ 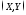называется

.

Для дискретной СВ: .

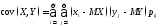Для непрерывной СВ: .

Формула для вычисления: .

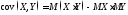Для независимых СВ .

Неудобством характеристики 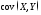является ее размерность (квадрат единицы измерения составляющих). От этого недостатка свободна следующая величина.

Определение. Коэффициентом корреляции СВ Х и Y называется

.

Для независимых СВ .

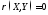Для любой пары СВ . Известно, что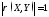тогда и только тогда, когда, где.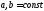

Определение. СВ Х и Y называются некоррелированными, если .

Связь между коррелированностью и зависимостью СВ:

− если СВ Х и Y коррелированы, т.е. 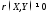,то они зависимы; обратное не верно;

− если СВ Х и Y независимы, то ; обратное не верно.

Замечание 1. Если СВ Х и Y распределены по нормальному закону и , то они независимы.

Замечание 2. Практическое значение 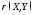в качестве меры зависимости оправдано лишь тогда, когда совместное распределение пары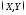нормально или приближенно нормально. Для произвольных СВХ и Y можно прийти к ошибочному выводу, т.е. может быть даже тогда, когдаХ и Y связаны строгой функциональной зависимостью.

Замечание3. В математической статистике корреляцией называют вероятностную (статистическую) зависимость между величинами, не имеющую, вообще говоря, строго функционального характера. Корреляционная зависимость возникает тогда, когда одна из величин зависит не только от данной второй, но и от ряда случайных факторов, или когда среди условий, от которых зависит одна или другая величина, имеются общие для них обеих условия.

Пример 4. Для СВ Х и Y из примера 3 найти .

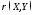Решение.

.

.

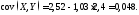
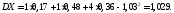
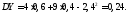
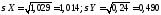Пример 5. Дана плотность совместного распределения двумерной СВ :

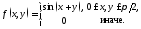
Найти .

Решение.

1)

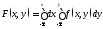
2)

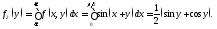
3)

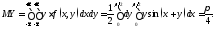
4)

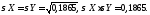
5)