2.6. Определение ускорений точек механизма методом планов ускорений

При помощи планов ускорений можно найти ускорения любых точек механизма. Для построения планов ускорений по аналогии с планами скоростей следует пользоваться их свойствами. Свойства такие же, как и у планов скоростей (см. подразд. 2.5), кроме третьего, где фигура, подобная одноименной жесткой фигуре на плане положений механизма, повернута на угол (180–) в сторону мгновенного ускоренияданного звена:

. (2.14)

Поскольку полные относительные ускорения состоят из геометрической суммы тангенциальных и нормальных составляющих, то концы векторов абсолютных ускорений обозначают буквами, соответствующими названию точек.

Определение ускорений рассмотрим также на примере механизма, представленного на рис. 2.3, а.

П р и м е р 4. Методом планов ускорений определить абсолютные и относительные ускорения точек звеньев и угловые ускорения звеньев механизма. Данные взять из условия примера 2.

Р е ш е н и е. Считая известными ускорения шарнирных точек (а_О1 = а_О2 = 0), помещаем их на плане ускорений в полюсе р_. Звено О₁А вращается равномерно, поэтому точка А имеет только нормальное ускорение , которое направлено по звену О₁А к центру вращения О₁ (рис. 2.3, в). Определяем его по формуле:

; м/с². (2.15)

Принимаем (произвольно) длину отрезка , изображающего вектор ускоренияточки А, равной 98,596 мм. Тогда масштаб плана ускорений, м/с²мм^-1,

; . (2.16)

Из полюса плана р_а откладываем параллельно звену О₁А в направлении от А к О₁.

Рассматривая движения точки В со звеном АВ, составляем векторное уравнение:

. (2.17)

В этом уравнении ускорение точки А известно по величине и по направлению. Определяем нормальное ускорение точки В относительно А:

м/с². (2.18)

На плане ускорений можно выразить отрезкоммм и отложить его параллельно звену АВ на плане из точки а в направлении от В к А (a₁ n₁), а затем из точки n₁ перпендикулярно звену АВ провести линию действия тангенциального ускорения до пересечения с линией хода ползуна (это и будет точка b).

Определяем ускорения точки В, м/с²:

;

(2.19)

.

Положение точки С на плане ускорений находим по свойству подобия (из пропорции):

; . (2.20)

Соединив ее с полюсом, определяем ускорение точки С, м/с²:

..

Для определения ускорения точки D рассматриваем движения точки D со звеньями СD и DO₂. Составляем векторные уравнения:

;

.

Определяем нормальные ускорения (ускорение точки С известно по величине и по направлению, а ускорение а_О2 = 0), м/с²:

;

;

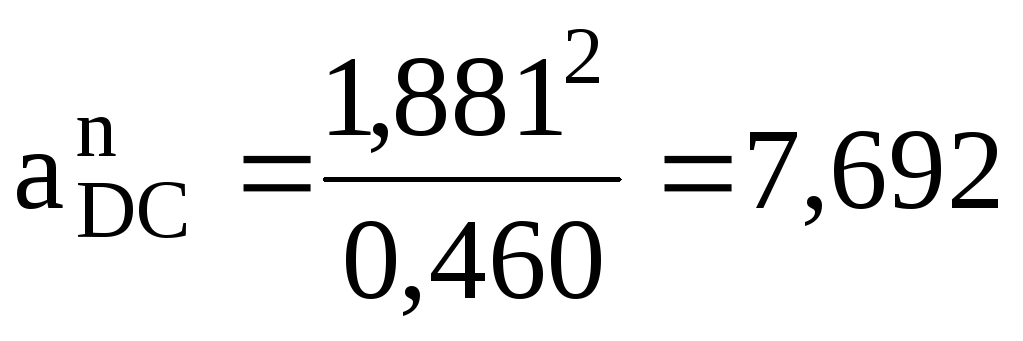От точки С плана ускорений параллельно звену DC в направлении от точки С к точке D откладываем вектор , изображающий ускорение, длина которого

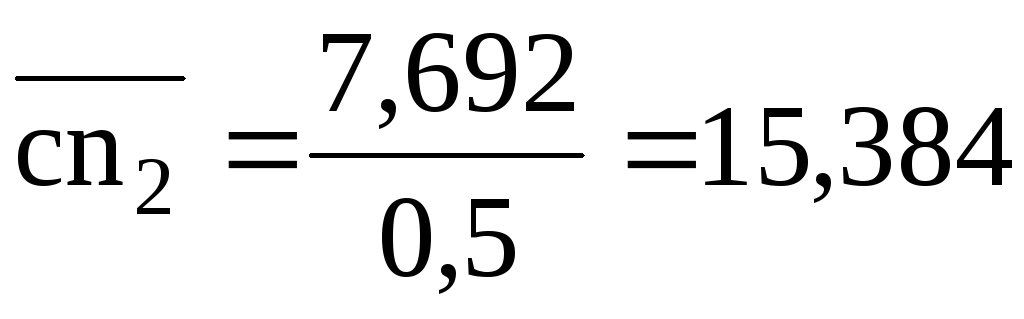мм. (2.21)

Из точки О₂ плана ускорений (из полюса р_а) параллельно звену DO₂ в направлении от D к О₂ откладываем вектор , изображающий ускорение, величина которого

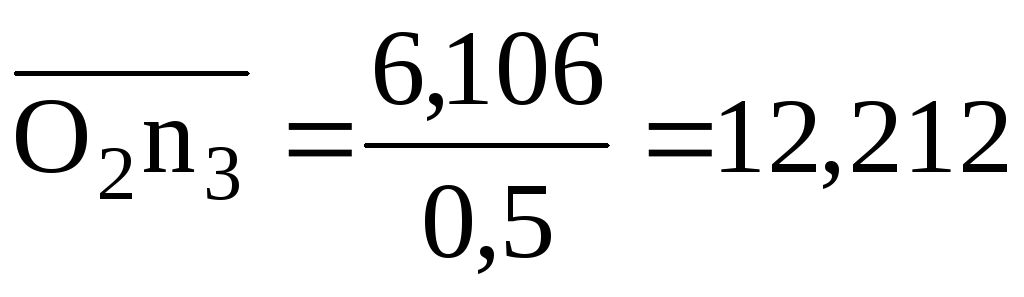мм.

Через точку n₂ проводим перпендикулярно звену CD линию действия тангенциального ускорения до пересечения с линией действия, проведенной из точкиn₃ перпендикулярно звену O₂D. На их пересечении получится точка d – конец вектора , изображающего ускорениеточкиD механизма:

м/с².

Определяем тангенциальные ускорения и относительные во вращении вокруг точек С и О₂, м/с²:

;

;

;

.

Из третьего свойства планов ускорений (свойства подобия) определяем места положений точек центров тяжести, а затем величины ускорений:

; ;

;

;

;

.

Определяем угловые ускорения звеньев.

Угловое ускорение ₁ ведущего звена О₁А, совершающего равномерное движение, равно нулю.

Угловое ускорение звена 2

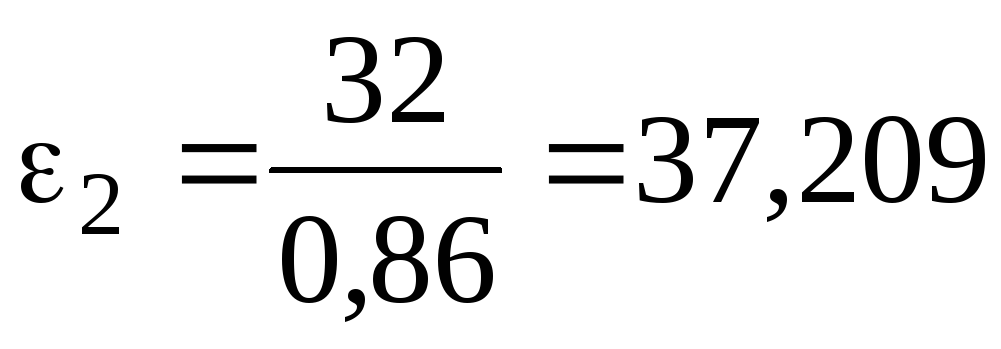с^-2.

Для определения направления углового ускорения ₂ звена 2 надо мысленно перенести вектор тангенциального ускоренияв точку В. В направлении этого вектора точка В вращается относительно точки А против часовой стрелки (см. рис. 2.3).

По аналогии определяем значения и направления угловых ускорений звеньев 4 и 5, с^-2:

(против часовой стрелки);

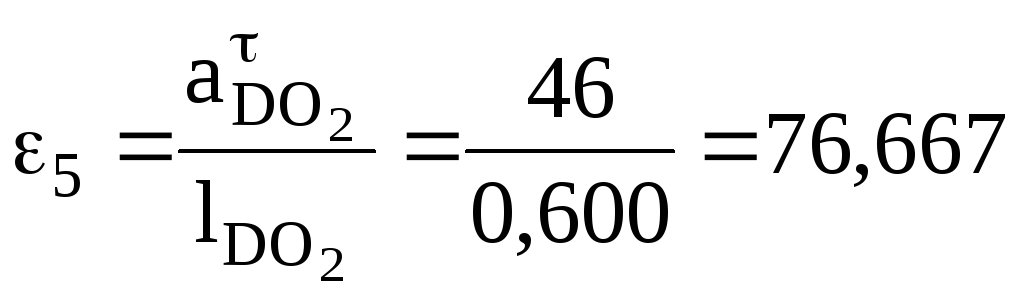(по часовой стрелке).

Примечание. Полученные значения линейных и угловых ускорений и скоростей всех точек механизма рекомендуется свести в таблицу.