4.7. Логические функции одной переменной

Разберем параметры таких функций:

n=1 – число переменных;

m=2 – число точек определения;

N=4 – число всех функций одной переменной.

Рассмотрим каждую функцию:

– нулевая функция.

– функция повторения.

– функция отрицания.

– единичная функция.

Таблица истинности функций одной переменной

Vi	x0
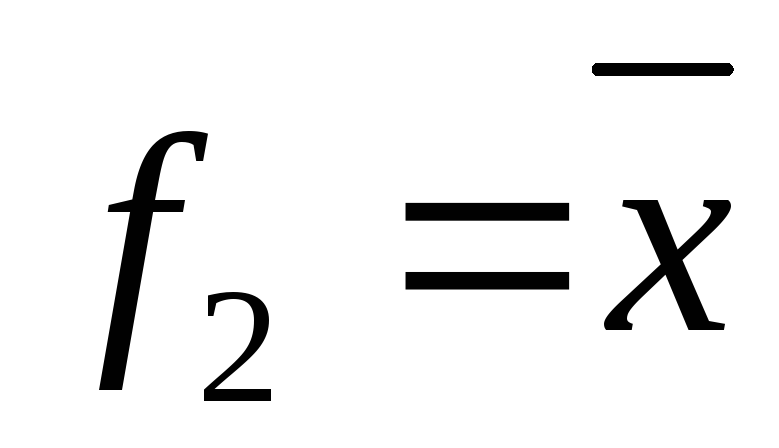
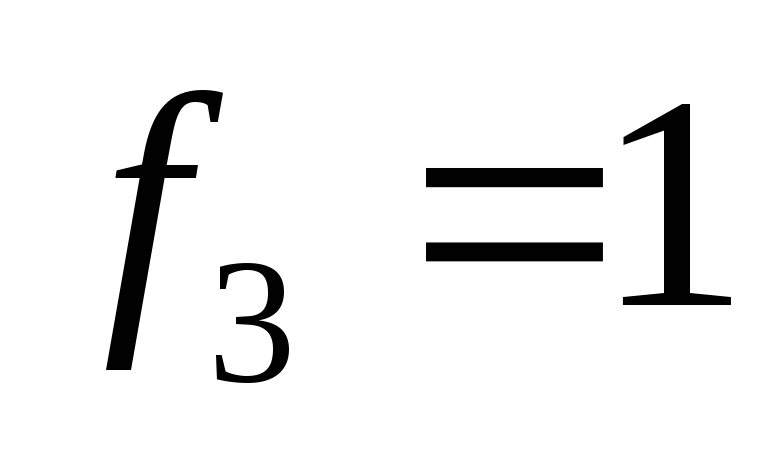
0	0	0	0	1	1
1	1	0	1	0	1

4.8. Логические функции двух переменных

Рассмотрим параметры функций:

n=2 – число переменных;

m=4 – число точек определения;

N=16 – число всех функций двух переменных.

Таблица истинности всех функций двух переменных

Vi	x1,x0
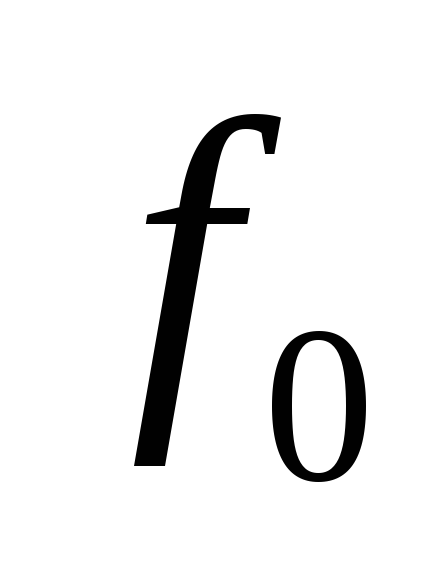
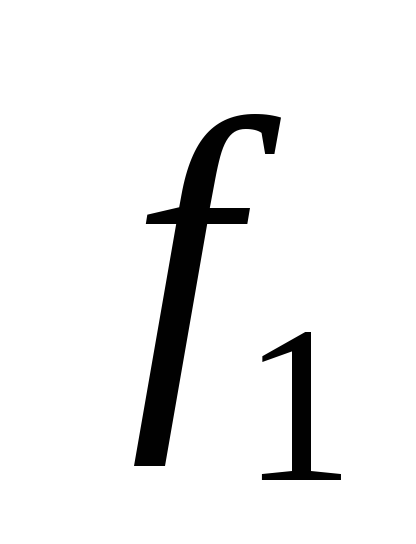
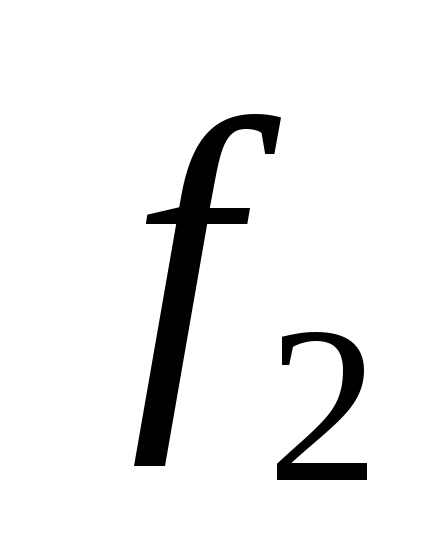
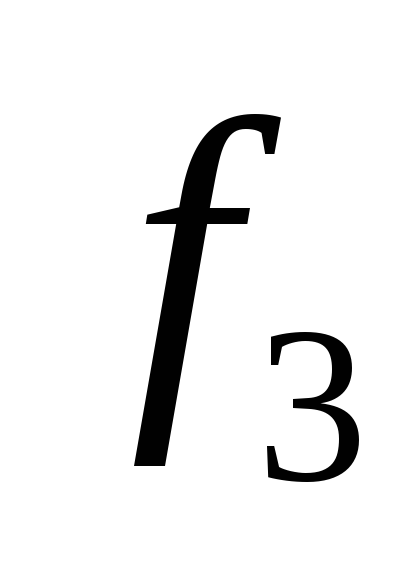
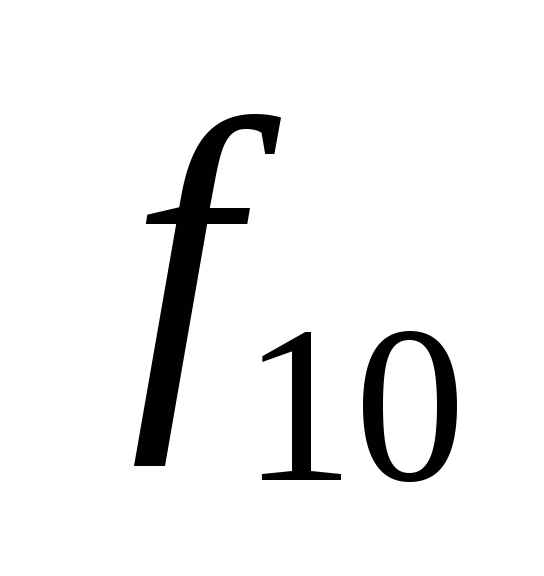
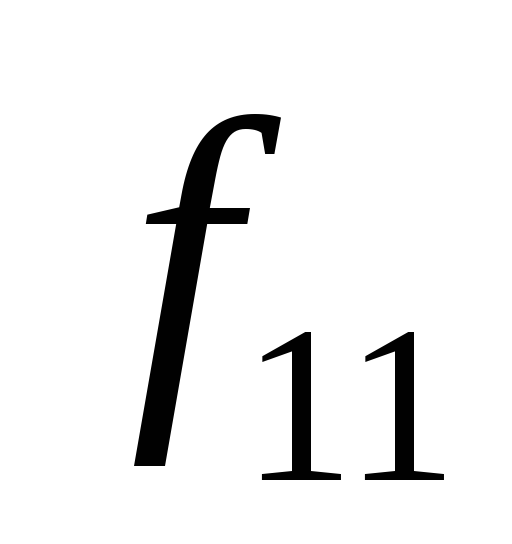
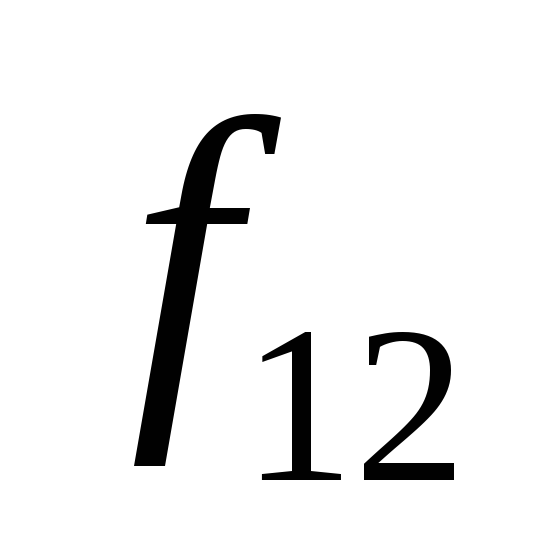
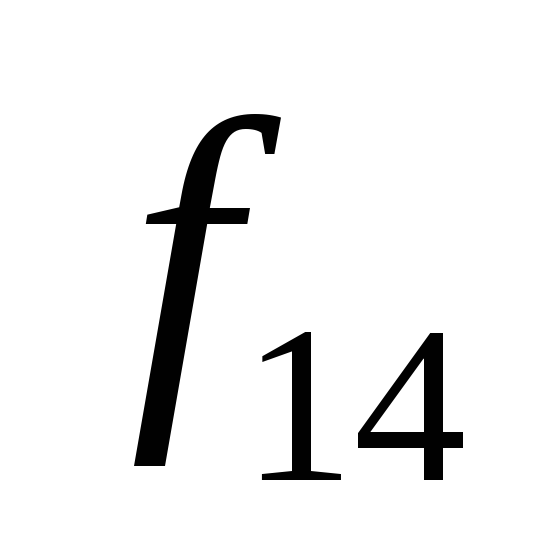
0	0 0	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
1	0 1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
2	1 0	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
3	1 1	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1

Значительный интерес представляют невырожденные функции, которые разберем подробно.

Функция логического умножения (конъюнкция).

– логическое умножение, описывает работу логического элемента И.

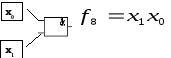Vi	x1,x0
0	0 0	0
1	0 1	0
2	1 0	0
3	1 1	1

Функция логического сложения (дизъюнкция)

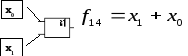
– логическое сложение, описывает работу логического элемента ИЛИ.

Vi	x1,x0
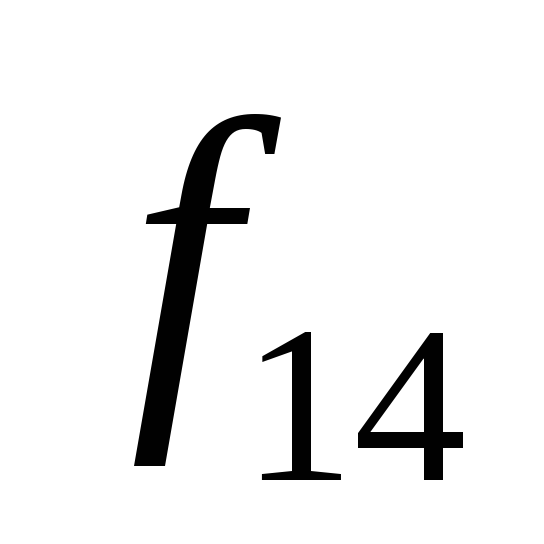
0	0 0	0
1	0 1	1
2	1 0	1
3	1 1	1

Функция сложения по модулю два(исключающее ИЛИ, неравнозначность)

– сложение по модулю два, применяется для арифметического сложения

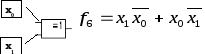Vi	x1,x0
0	0 0	0
1	0 1	1
2	1 0	1
3	1 1	0

Функция Пирса, логическое сложение с отрицанием, отрицание дизъюнкции (стрелка Пирса, ИЛИ-НЕ)

– логическое сложение с отрицанием ИЛИ-НЕ

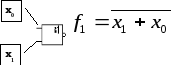Vi	x1,x0
0	0 0	1
1	0 1	0
2	1 0	0
3	1 1	0

Функция Шеффера, отрицание логического умножения (штрих Шеффера И-НЕ)

– логическое умножение с отрицанием И-НЕ

Vi	x1,x0
0	0 0	1
1	0 1	1
2	1 0	1
3	1 1	0

Функции двух переменных исключительно важны в силу того, что любая логическая функция n переменных может быть получена из них методом суперпозиции – подстановкой этих функций в место переменных в другие функции.

4.9. Теоремы разложения

В теории логических функций особо важное значение имеет теорема разложения Шеннона: любую функцию F(v)можно разложить по переменнойx_pв форме:

По принципу двойственности получается двойственная теорема разложения:

С теоремой разложения связаны тождества