1.5. Условия оптимальности решения.
Условия оптимальности решения бывают двух типов: необходимые и достаточные.
Необходимые условия оптимальности.
Общая формулировка необходимых условий: если из утверждения А всегда следует утверждение В, то В необходимо для А.
Применительно
к задаче оптимизации: из утверждения А
(
- лучший элемент множестваD)
следует утверждение В (
- лучший элемент множестваL,
принадлежащего D
и образующего окрестность
)
(рис.1.7).
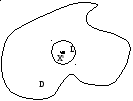
Рис. 1.7
Таким
образом локальная
неулучшаемость
(
- лучший элемент среди допустимых
элементов своей окрестности) являетсянеобходимым
условием для того, чтобы
был оптимальным решением.Иными
словами, для того чтобы X
был оптимальным решением на множестве
D,
необходимо, чтобы X
был оптимальным решением на множестве
L,
принадлежащем D
и образующим окрестность точки X.
Как правило, множество L
выбирают так, чтобы на нем критерий и
ограничения исходной задачи точно
совпадали с критерием и ограничениями
вспомогательной упрощенной задачи, для
которой решение можно выделить с помощью
некоторых уравнений. В этом случае
уравнения, выделяющие локально
неулучшаемое решение, оказываются
необходимыми условиями оптимальности
исходной задачи. Обычно упрощенную
задачу строят посредством линеаризации
исходной в окрестности искомого
оптимального решения.
Достаточные условия оптимальности.
Общая
формулировка достаточных условий: если
из утверждения В всегда следует
утверждение А, то В достаточно для А.
Применительно к задаче оптимизации из
утверждения В (решение
является лучшим на множествеV,
включающем множество D,
причем
принадлежитD)
всегда следует утверждение А (
- лучший элемент множестваD)
(рис.1.8)).
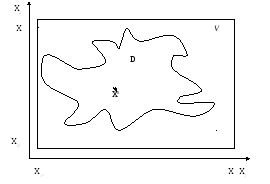
Рис. 1.8
Таким
образом, неулучшаемость на множестве,
охватывающем D,
вместе с принадлежностью к D,
является достаточным условием того,
чтобы
было искомым оптимальным решением.
Иными словами, для того, чтобы X был оптимальным решением на множестве D, достаточно чтобы X был оптимальным решением на множестве V, включающем множество D, и принадлежал множеству D.
Использование достаточных условий целесообразно при сложноорганизованных множествах допустимых решений D, что затрудняет решение задачи, расширенное же множество V оказывается гораздо проще.
Например
множество D,
представленное на рис. 1.8 целесообразно
заменить областью V, которая представляет
собой прямоугольник, включающий в себя
область D
и может быть описана автономными
ограничениями вида
(см. рис. 1.8)
2. Определение максимума функции одной переменной.
2.1. Постановка задачи. Методы решения оптимизационных задач.
В данном случае в критерии оптимальности присутствует только одна варьируемая переменная. На нее могут быть наложены только автономные ограничения и постановка задачи принимает вид:
(2.1)
(2.2)
В соответствии с
теоремой Вейерштрассе всякая функция
,
непрерывная на замкнутом и ограниченном
множестве (
),
достигает на нем своего наибольшего и
наименьшего значения. Функция
выпукла
на
,
если она имеет на этом множествеединственный
максимум.
Выпуклая функция обладает тем свойством,
что, если через две любые принадлежащие
ей точки провести прямую (с координатами
и
),
то любая промежуточная точка этой прямой
не будет превышать значение функции
при том жеХ
(рис.2.1).
Для выпуклой функции справедливо
выражение:
,
где
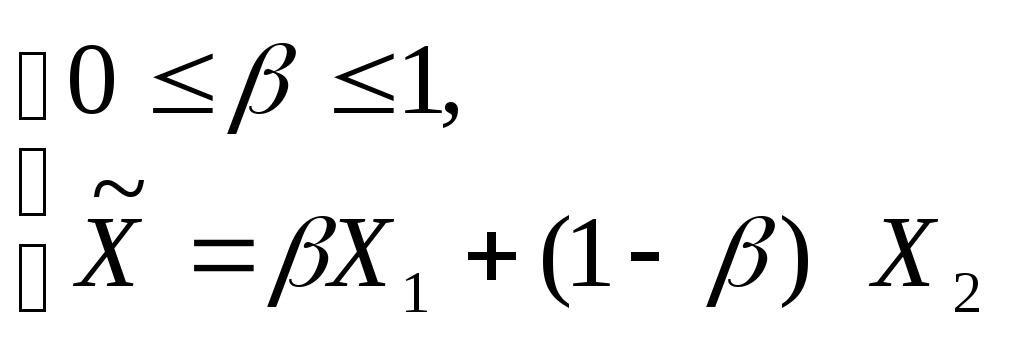
Если функция не выпукла (неунимодальна), то она будет иметь несколько точек максимума, причем значение функции в этих точках будет различным (рис. 2.2)
В
этом случае точка, соответствующая
наибольшему значению функции (точка
на рисунке) называется точкой
глобального максимума,
а остальные точки (
,
,
,
)
– локальными
максимумами функции.
Рис.2.1
Все методы решения оптимизационных задач, в том числе методы определения максимума функции одной переменной делятся на:
Аналитические, основанные на необходимых или достаточных условиях оптимальности, причем достаточные условия применяются только в случае сложноорганизованных областей допустимых значений D.
Численные, которые представляют собой вычислительную процедуру, обеспечивающую последовательное уточнение решения от некоторого начального приближения до максимума с заданной допустимой погрешностью.
2.2. Аналитический метод решения задачи. Условия максимума функции одной переменной.
Пусть
- непрерывная и дважды дифференцируемая
функция при
иX0
- точка предполагаемого маусимума
функции. Для того, чтобы при X0
функция
достигала max необходимо, чтобы при любом
другом Х,
сколь угодно близком к X0,
т.е.
,
выполнялось соотношение
(2.3)
Разложим
в ряд Тейлора в окрестности точкиX0
(2.4)
При небольших Х, членами, содержащими приращения в степени больше единицы можно пренебречь и тогда из (2.4) следует:
.
(2.5)
Подставляя (2.5) в (2.3) окончательно получаем необходимое условие максимума функции одной переменной:
(2.6)
При использовании этого условия могут возникнуть два варианта:
1.
- внутренняя точка интервала допустимых
значений (рис. 2.3). В этом случае знакХ
не определен и для выполнения условия
(2.6) необходимо
(2.7)
При
этом знак разности (2.3) определяется
знаком первого отброшенного члена ряда
Тейлора, т.е. знаком
.
Поэтому необходимое условие max (2.7)
дополняется условием
(2.8)
2.
- граничная точка интервала
.
В этом случае знакХ
определен
(рис. 2.4) и для расчетов будем использовать
выражение (2.6).
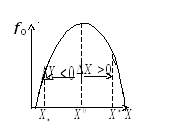
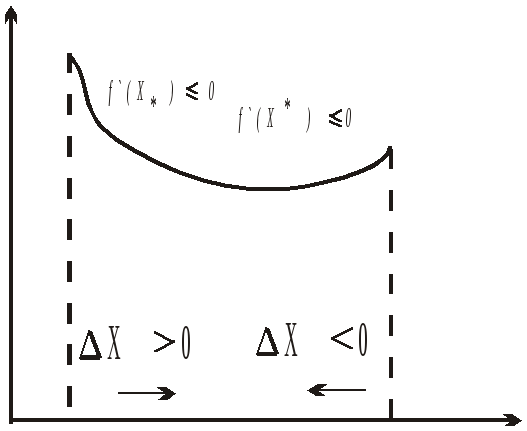
Рис.2.3. Х* Х* Х
Рис. 2.4.
Сформулируем правила применения необходимых условий максимума функции одной переменной.
Определяют все корни уравнения (2.7), являющиеся внутренними точками отрезка
и для каждого из них проверяют условие
(2.8). Удовлетворяющие ему корни являются
точками локальных максимумов целевой
функции.Рассчитывают значение функции
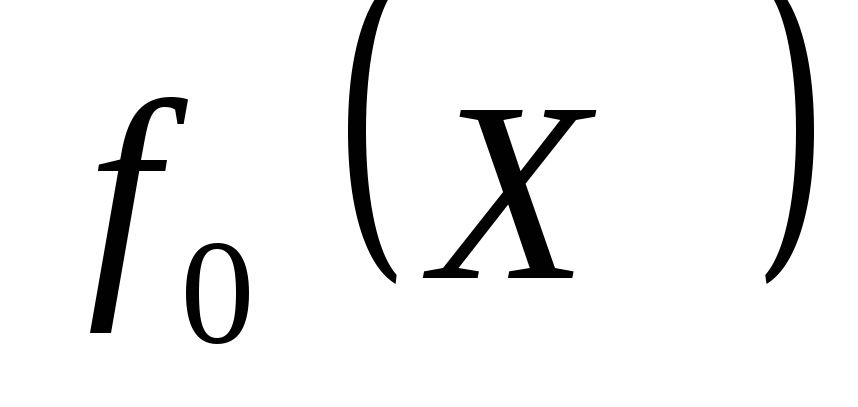в этих точках и сравнив их между собой
определяют глобальный максимум.Если среди корней уравнения (2.7), нет значений, принадлежащих множеству допустимых решений, необходимо проверить граничные точк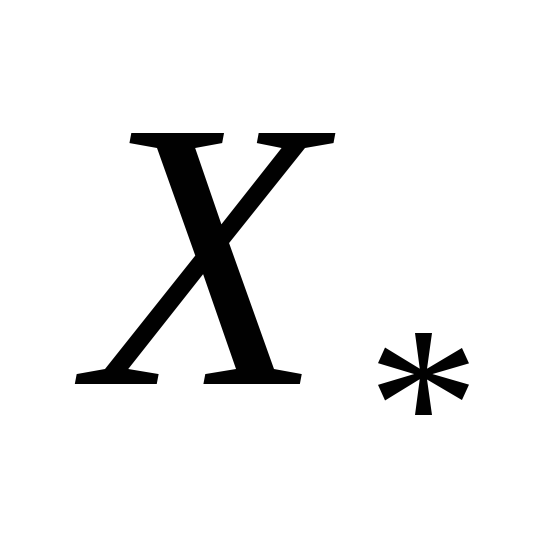и
и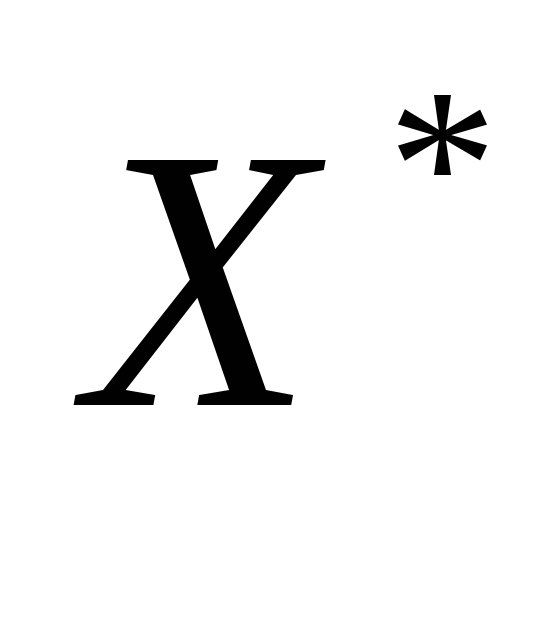
с использованием условия (2.6).
Пример.
Определить максимум функции
при
а)
,
б)
,
в)
;
а)
X0
= 0.6, внутренняя точка отрезка
,
следовательно, знак ΔX
не определен и необходимо проверить
выполнение условия (2.8).
0
Условие (2.8) выполняется.
Ответ:
б)
,
проверим
- нижняя граница отрезка
,
следовательно,Х
0.
Проверяем выполнение условия (2.6).
<
0.
Условие
(2.6)
выполняется, т.е.
.
в)
.
ПроверимХ
= 0.5 – верхняя
граница отрезка
,
следовательно,Х
0.
Проверяем
выполнение условия (2.6):
0
Условие
(2.6) выполняется, т.е.
