9.5. Оптимизация режима в аппарате периодического действия.

Здесь сырьё периодически загружают в аппарат, а готовый продукт периодически выгружают из него. Продолжительность цикла, а также закон изменения управляющих воздействий за время цикла подлежат оптимальному выбору.

Пусть целевая функция ₀(,) определяет мгновенную продуктивность процесса.

Обозначим через  - продолжительность загрузки и выгрузки, а T – продолжительность работы аппарата в каждом цикле. Учтём также, что загрузка и выгрузка связаны не только с затратами времени, но и с затратами трудовых и материальных ресурсов на сырьё, очистку аппарата и т.д. Величину этих затрат, которые обычно не зависят от длительности цикла, обозначим через А.

Тогда критерий оптимальности задачи запишется в виде:

I = dt – А )  max (9.13)

Максимум этого выражения нужно найти при условиях (9.4), записанных в форме дифференциальных уравнений и при фиксированных начальных значениях переменных состояния.

X_(0) = X_0  = 1,…, m (9.14)

Что касается конечных значений этих переменных X(T), то, как правило, некоторые из них фиксированы, а остальные свободны.

X_(T) = X_T  = 1,…, k; k < m (9.15)

Условия типа автономных ограничений (9.2) и функциональных ограничений (9.5) также могут иметь место. Выбору подлежат управляющие воздействия (t) и рабочее время цикла T.

9.6. Календарное планирование работы аппарата

В предыдущих задачах предполагалось, что собственные характеристики аппарата и условия, в которых он работает, неизменны. В действительности же и те и другие могут изменяться во времени. Например, по некоторому закону могут изменяться заданная производительность и поставки сырья. Как правило, эти изменения происходят значительно медленнее, чем переходные процессы в аппарате, поэтому связи между состояниями X и управлениями U задают в квазистатической форме.

(,,t) = 0  = 1,…, m (9.16)

Производительность аппарата для каждого момента времени t должна лежать в заданном интервале

P_(t)  P (,) P^(t) (9.17)

Если в аппарате имеются ёмкости, то на уровень в них наложены ограничения H_i  H_i (t)  H_i^  t

_

H_i = h_i (,, t) i = 1,…, l, (9.18)

где h_i (,, t) – разность потоков, втекающих вi-ю ёмкость и вытекающих из неё в момент t.

Если через T_n обозначить интервал планирования, то критерием оптимальности может служить интегральная эффективность аппарата за этот интервал.

I = dt  max (9.19)

9.7 Оптимальный режим работы параллельно включенных агрегатов: распределение нагрузок.

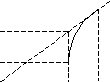
Задача формулируется следующим образом (рис.9.1):

P_i(x^_i)

_

P_i(x^_i)

-

P_i(x^_i)

P_i(x_i*)

X_i

Рис. 9.1. Рис. 9.2.

• требуется выбрать нагрузку каждого из агрегатов и состав работающих агрегатов, включённых параллельно, если общая нагрузка (суммарный расход сырья) задана, а общая производительность должна быть максимальной.

С=,

где X_i – нагрузка на каждый агрегат i=1,2…n, С – суммарная нагрузка,

Р=,

где Р_i – производительнлсть i-го агрегата i=1,2…n, Р – суммарная производительность.

Для каждого из агрегатов известна нагрузочная характеристика – зависимость производительности P_i от расхода сырья X_i (рис. 9.2).

Тогда критерий оптимальности запишется в виде:

P = (X_i)  max (9.20)

а ограничения X_i = 0 или X_i X_i  X_i^.

Первое из этих условий относится к случаю, когда агрегат выключен, а второе – когда он работает. Эти условия удобно переписать, исключив слово «или», для чего вводится целочисленная переменная Vi.

V_i=

Обозначив X_i = V_i, получаем критерий оптимальности

P =  (9.21)

V_i=, i=1…n (9.22)

D=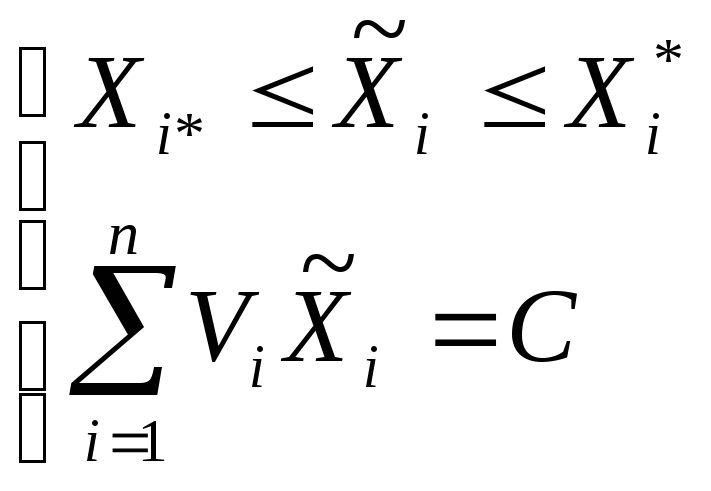 (9.23)

Условие (9.23) соответствует выполнению требования суммарной нагрузки по сырью. Наличие целочисленных переменных значительно усложняет решение этой задачи. Рассмотрим некоторые варианты постановки задачи распределения.