5.3. Метод динамического программирования. Принцип оптимальности Беллмана.

Предназначен для решения задачи (5.1) – (5.4) оптимизации многостадийных процессов.

При заданном начальном состоянии процесса стратегия управленияоднозначно определяет состояние многостадийного процесса на всех стадиях, т.к. любоеможно последовательно рассчитать по уравнению связи(5.11)

Беллман сформулировал следующий принцип оптимальности, который позволяет определить оптимальную стратегию управления без использования метода неопределенных множителей Лагранжа:

Оптимальная стратегия обладает тем свойством, что какова бы не была последовательность , приводящая к состоянию, управлениедолжно быть оптимальным по отношению к этому состоянию как исходному. Поясним принцип оптимальности Беллмана на примере похода в лес за грибами.

В процессе поиска грибов человек перемещается по лесу достаточно хаотично, руководствуясь соображениями типа: туда пойду – там березки, туда не пойду – там овраг. Однако, приняв решение возвращаться домой, грибник старается с этого момента, т.е. из промежуточного состояния X_i-1, двигаться оптимально, чтобы добраться домой за наименьшее время, в какую бы точку леса его ни привело управление своим движением на предыдущих этапах.

Функцией Беллмана называется оптимальное значение целевой функции для стадий процесса сi-й до n-ой включительно. Оно, очевидно, должно зависеть от состояния объекта .

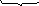
(5.12)

Выделим в правой части выражения (5.12) первое слагаемое под знаком max

, (5.13)

где (5.14)

Подставляя вместов соответствии с уравнением связи (5.11), с учетом того, чтополучаем уравнение Беллмана.

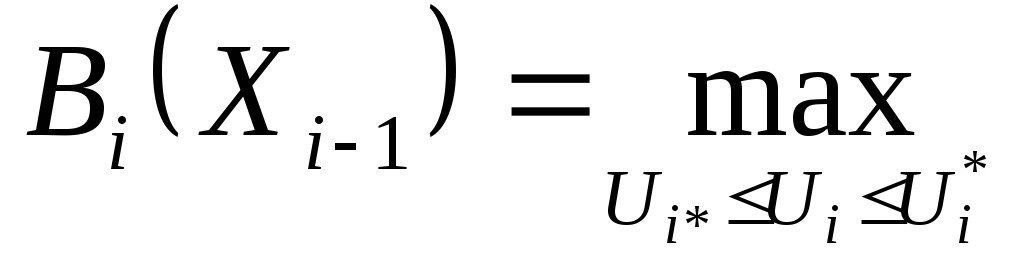
(5.15)

Очевидно, что после окончания процесса, управление отсутствует, т.е.

(5.16)

Уравнение (5.15) совместно с граничным условием (5.16) позволяет решать задачи оптимизации многостадийных процессов от конца к началу.

Пример.

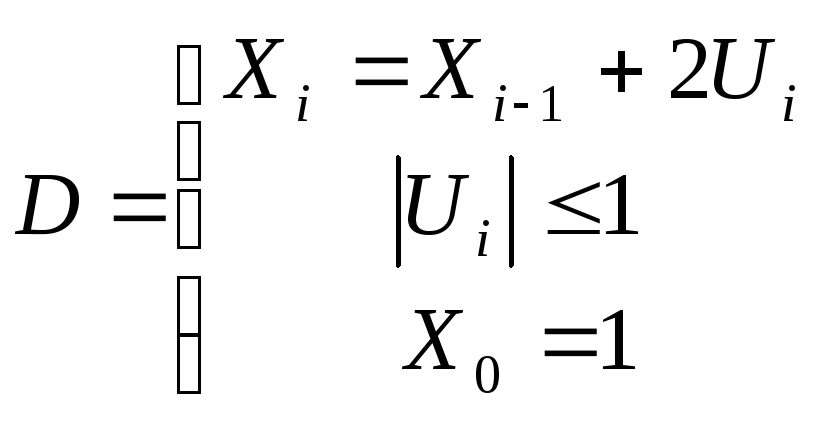
Так как в данном случае n=3, то выражение (5.16) имеет вид

Составляем функцию Беллмана для последнего, т.е. третьего этапа

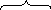
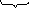
Для обеспечения max (X₂ + U₃) необходимо, чтобы

Так как , то вышеуказанное условие будет выполняться только при ∆U₃ < 0, т.е. на верхней границе управления U₃⁰ = 1.

Следовательно, B₃(X₂)=X₂+1. Эти же рассуждения, как показано ниже, справедливы и для расчета U2 и U1.

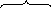
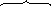
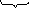
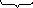
Так как 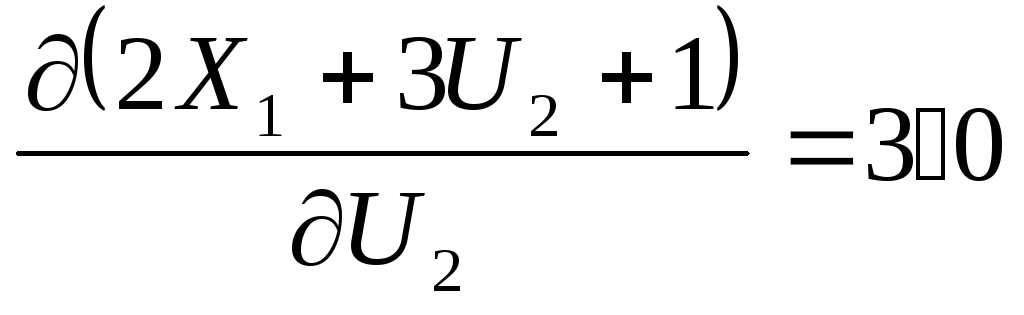, то необходимо выполнение условия, т.е.- верхняя граница управления, откуда следует:

+4

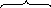
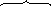
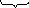
, т.к. по условию задачи , то

,

Так как 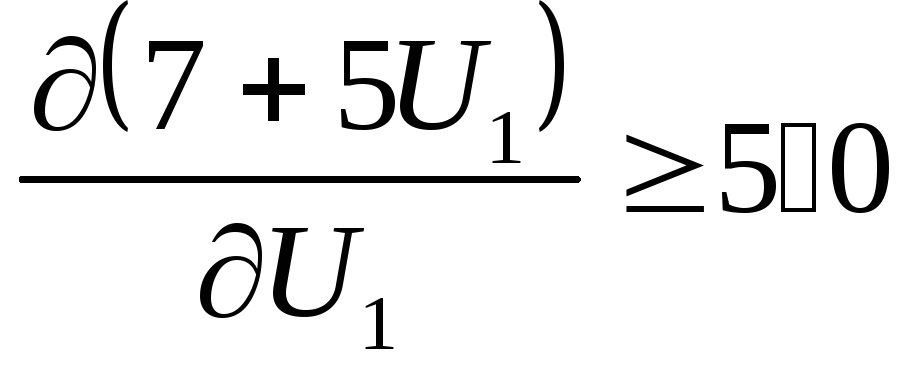, то необходимо ΔU₁<0, т. е. U₁⁰=1 – верхняя граница управления.

; ;;

Таким образом, задача решена.

5.4. Задача определения оптимального пути на сетевом графике (графе).

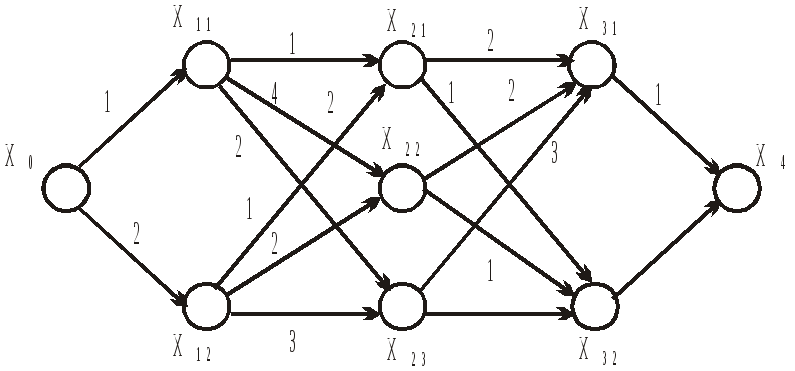
Сетевые графики используются для решения дискретных задач оптимизации многостадийных процессов, в которых переменные управления могут принимать только несколько определенных значений. Пример сетевого графика представлен на рис. 5.3.

К

аждому из возможных состояний процесса соответствует кружок, стрелки, выходящие из кружка, соответствуют различным допустимым значениям управлений.

Рис. 5.3.

Задача заключается в том, чтобы из заданного начального состояния попасть в заданное конечное состояние, следуя тем путем для которого суммарное управление, т. е. сумма цифр, поставленных над дугами графа (значений) была максимальна. Таким образом, структурная схема данной задачи, представленная на рис. 5.4, аналогична структурной схеме задачи оптимизации многостадийных процессов (см. раздел 5.1).

U₄

4

X₄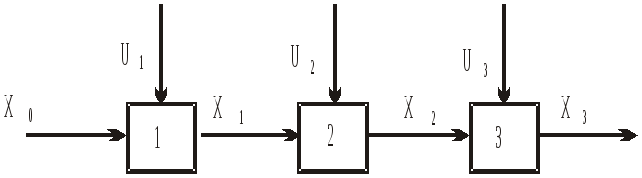

Рис. 5.4.

Рассмотрим решение поставленной задачи на примере сетевого графика (графа), представленного на рис 5.5.

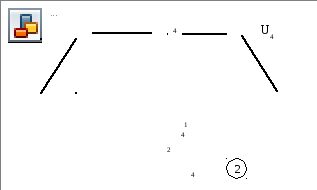
Рис. 5.5.

Найти при котором. Задача решается от конца сетевого графика к началу, т. е. справа налево.

1) Рассмотрим все состояния четвертой стадии. Согласно принципу оптимальности Беллмана, в каком бы из них процесс не оказался, далее следует действовать оптимально. В данном случае управление единственно для каждого, К=1,2,3,4, а значит оно и оптимально. Ему соответствует единственное, а значит и максимальное значение управления. Это значение мы впишем внутрь кружка соответствующего каждому из состоянийи обозначим:,,,, а дугу, соответствующую оптимальному движению в, подчеркнем штриховой линией и будем называть ее условно оптимальным управлением (оптимальным при условии, что мы оказались в данном состоянии).

2) Переходим к следующей, т.е. третьей стадии. Для каждого из возможных состояний ,К=1,2,3,4, ищем оптимальное решение, приводящее к c максимальным значениемU на двух последних стадиях. Для каждого из этих состояний возможны три управления. Так для первого управления из состояния получаеми, пять записано в кружочке, это самое лучшее, что можно получить, если мы окажемся в. Т.о. первое управление даствторое 8 и третье 4. Следовательно, оптимальным по отношению кявляется первое управление, а максимальное значение. Обозначим его черези занесем 9 внутрь кружка, а условно оптимальное управление подчеркнем штриховой линией. Аналогично найдем условно-оптимальное управление по отношению к состояниюкак к начальному и подсчитаем максимальное управление для этого состоянияB₃ (X₂₂) = 7. Для остальных состояний третьей стадии получаем ,- запишем эти значения в кружочках.

3) Переходим ко второй стадии и для каждого состояния К=1..4 подсчитаем максимальное управление при условии, что это состояние является начальным и определим соответствующее ему условно-оптимальное управление. Отметим, что при этом мы будем пользоваться лишь функцией, значение которой уже рассчитано на предыдущем этапе и записано внутри кружков соответствующих. ПолучимВ₂(X₁₁)=7+9=16, В₂(X₁₂)=5+7=12, В₂(X₁₃)=4+9=13, В₂(X₁₄)=3+8=11.

4) Для первой стадии, т.е. для начального состояния , выбор оптимального управления производится один раз, т.к. это состояние задано, причем условно-оптимальное решение на этот раз будет искомым оптимальным решением поставленной задачи, а величинапредставляет собой максимальное суммарное управление. Найденное управление ведет в состояние, для которого управлениеуже найдено и т.д. Таким образом, задача решена. В результате на сетевом графике получим оптимальную траекторию (подчеркнута сплошной двойной линией), обеспечивающую перевод процесса из заданного начального состоянияX₀ в заданное конечное состояние X₄ с max затратами на управление

Очевидно, что такая задача была поставлена только для пояснения принципа расчета сетевых графиков. В реальных задачах требуется обеспечить min расходы на суммарное управление, однако порядок расчета при этом не изменится.

Обобщим процедуру решения примера. Отметим, что величина оптимального суммарного управления подсчитывалась как максимальная по суммы двух слагаемых: управления наi-й стадии и максимум управления, подсчитанного ранее при условии, что мы попадаем в состояние. Т.о. имеем уравнение Беллмана:

Для рассмотренного примера имеем:

, ,,,.

, ,,.