1.2 Баланс мощностей в простейшей цепи постоянного тока.

При протекании электрического тока по участку цепи с сопротивлением R происходит преобразование электрической энергии в тепловую. Количество электрической энергии W, преобразуемой в тепловую энергию за время t, определяется по закону Джоуля-Ленца.

W = I²Rt

Мощность P представляет собой количество энергии в единицу времени

P =

Основными единицами измерения мощности являются [Вт, кВт].

Рассмотрим баланс мощностей в простейшей цепи постоянного тока. Для этого все члены уравнения равновесия напряжений (1.2) умножим на величину тока в цепи.

IE = I² R₀ + I² R_л + I² R (1.5)

Полученное выражение (1.5) называется уравнением баланса мощностей.

Произведение IE представляет собой полную электрическую мощность P₁, развиваемую генератором. Рассмотрим слагаемые в правой части выражения (1.5) Обозначим их соответственно

∆P_г = I² R₀ - потери мощности внутри генератора.

∆ P_л = I² R_л - потери мощности в линии передач.

Р_{2 =} I²R - полезная мощность, потребляемая нагрузкой.

Подставляя полученные выражения мощностей в уравнение (1.5)получаем:

P_{1 =} ∆ P_г + ∆ P_{л +} Р₂

Баланс мощностей рассмотренной цепи можно проиллюстрировать в виде энергетической диаграммы (рис. 1.3.):

Рис. 1.3. Энергетическая диаграмма электрической цепи.

P₂

Коэффициентом полезного действия (КПД) электрической цепи называют отношение полезной мощности Р₂, потребляемой нагрузкой к полной мощности Р₁, развиваемой генератором , т.е.

η =

КПД современных энергетических установок достигает 95%.

1.3. Последовательное соединение сопротивлений.

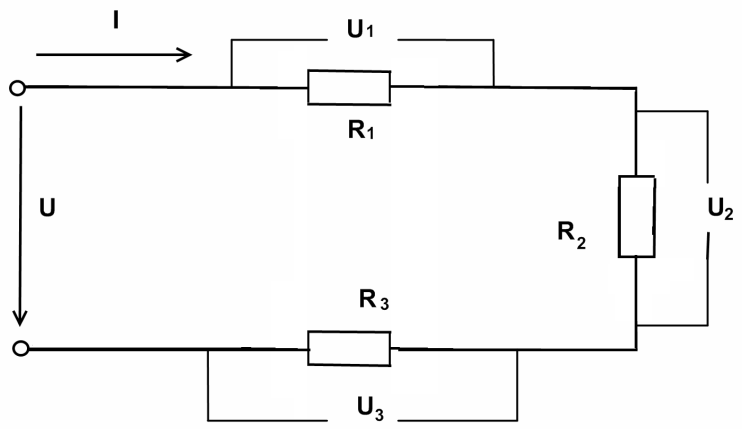
Рис. 1.4.Последовательное соединение сопротивлений.

При последовательном соединении сопротивлений через все элементы цепи протекает один и тот же ток (рис. 1.4.). К таким цепям может быть применен второй закон Кирхгофа: алгебраическая сумма ЭДС, действующих в цепи, равна сумме падений напряжений на всех сопротивлениях, входящих в цепь:

∑Е = ∑ IR

Применительно к рассмотренной цепи, второй закон Кирхгофа может быть записан в следующем виде:

U = U₁ + U₂ +U₃;

IR_э = IR₁ +IR₂ + IR₃ (1.6)

Сокращая все члены уравнения (1.6) на величину тока I получим выражение для определения общего (эквивалентного) сопротивления цепи R_э

R_э = R₁ + R₂ + R₃

Таким образом, чем больше сопротивлений включаются последовательно друг другу, тем больше величина общего (эквивалентного) сопротивления цепи.

Ток на любом участке цепи будет один и тот же: I =

Напряжение на отдельных элементах цепи распределено прямо пропорционально их сопротивлениям:

Недостатками этого вида соединений являются зависимость работы приемников друг от друга, т.к. при отключении одного из элементов ток прерывается во всей цепи и зависимость напряжений на отдельных участках цепи от их сопротивлений.

Поэтому на практике последовательное соединение сопротивлений применяется крайне редко. Единственным широко известным примером такого соединения является ёлочная гирлянда.