Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный архитектурно-строительный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Пособие_Бедарев_Федорова_Федорченко

.pdf

Скачиваний:

Добавлен:

09.04.2015

Размер:

1.64 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1614 15 16 > Следующая >>>

«входят» в линию разрыва и приносят на нее информацию о решении, в последнем случае характеристики «выходят» из разрыва и уносят информацию в окружающую среду. В газовой динамике существование таких решений запрещает второй закон термодинамики, предписывающий неубывание энтропии замкнутой системы. В связи с этой аналогией в вычислительной математике используют термин «энтропийное» решение. При построении разностных схем для уравнения (3.34) надо следить за тем, чтобы в процессе решения не появлялись нефизичные, т.е. «неэнтропийные» решения. Доказано, что решения, полученные с помощью монотонных разностных схем, являются энтропийными.

Второй способ построения правильных «энтропийных» решений – это использование «псевдовязкости», т.е. искусственного сглаживания решений уравнения (3.39) путем введения в

него дополнительного слагаемого, например

¶u + u	¶u	= ε	¶2u	,	(3.48)
¶t	¶x		¶x2

где ε – малый параметр, имеющий физический смысл коэффициента вязкости. При ε ® 0 уравнение (3.48) переходит в (3.39), следовательно, решение уравнения (3.39) может быть получено как предел решений (3.48).

Приведем еще один – третий пример Лакса для уравнения (3.39) с начальными данными:

	1,	x £ 0
ϕ0			(3.49)
ϕ0	= 1 - x, 0 < x < 1		(3.49)
		x ³ 1
	0,	x ³ 1

Точное решение задачи при t < 1 имеет вид:

1,		x £ t
	(1 - x)				1, x £1 + t / 2
u(x, t) =			,	t < x <1,	u(x, t) =
	1					+ t / 2
		- t			0, x ³1
0,		x ³		1

При 0 < t < 1 решение непрерывно. В момент времени t = 1 происходит градиентная катастрофа, т.е. производная решения

130

обращается в бесконечность, и при t > 1 решение является разрывным. Это решение моделирует процесс образования ударных волн и поэтому является хорошим тестом для уравнений газовой динамики.

В заключение приведем TVD-схему для уравнения (3.39), которую можно использовать для расчетов разрывных решений.

Пусть F = u 2 2 . С учетом направления поток раскладывается на две составляющие F = F − + F + ,

u 2

, u > 0

−

u 2

, u < 0

где

. Аппроксимация повы-

0, u < 0

0, u > 0

шенного порядка строится по следующим формулам:

¶F (u)

−

Fj + 12

- Fj − 12

+ Fj + 12

- Fj − 12

¶x

F j + 1

{(1 − k )

(F j +1 )},

= F j +1 −

(F j +1 )+ (1 + k )

−

= F j

{(1 - k )D (Fj )+ (1 + k )D

(Fj )}

F j + 1

−

D+ (Fj ) = Fj +1 - Fj ,

D− (Fj ) = Fj - Fj−1 .

Для сохранения монотонности решения в областях разрывов и локальных экстремумов для схем повышенного порядка аппроксимация снижается путем применения ограничителей. Один из

возможных – это замена операторов + и D− операторами δ + и δ − соответственно:

signD+ signD− £ 0

δ + = min(

D+

, Q

D−

)

signD+ signD− ³ 0

signD+ signD− £ 0

δ − = min(

D−

, Q

D+

)

signD+ signD− ³ 0

131

k – параметр схемы, от которого зависит порядок аппроксимации: второй при k = – 1, третий при k = 1/3, Θ лежит в пределах

1 ≤ Θ ≤ 3 − k .

1 − k

11.8. Волновое уравнение

Типичным представителем уравнений гиперболического типа является так называемое волновое уравнение, описывающее распространение различных волн:

utt = g 2 (x, t )uxx + f (x, t ).

(3.50)

Пусть требуется решить уравнение в области G: x (0,1),

t (0, T ) .

Дополним уравнение начальными данными

u(x, 0) = σ1 (x); ut (x, 0) = σ 2 (x)

(3.51)

и краевыми условиями

p0u (0, t) + p1 ux		(0, t) = A(t),
s0 u (1, t) +		(3.52)
	s1 ux (1, t ) = B(t).

Явная конечно-разностная схема

Для приближенного решения будем использовать конечноразностный метод. Для этого введем в области G разностную сетку, в качестве которой используем совокупность точек пере-

сечения прямых x = ih, t = jτ, i = 0, 1, ..., N; j = 0, 1, ..., M, где h и

τ – шаги сетки по пространственной и временной координатам. Если положить, что шаги h и τ связаны соотношением τ = rh, r = const, то сетка будет зависеть только от одного параметра h.

Через uij обозначим значение сеточной функции в точке (xi, t j). Аппроксимируем входящие в (3.50) – (3.52) производные конечно-разностными соотношениями второго порядка точности:

∂2u

(x , t j

) ≈

u(x , t j+1 ) − 2u(x , t j ) + u(x , t j+1 )

j+1 − 2u

j + u

j−1

∂t 2

τ 2

∂2u

u(x

, t j ) − 2u(x , t j ) + u(x

, t j )

u j

− 2u j

+ u j

∂x2

(x , t

) ≈

i−1

i+1

i−1

132

определено начальными

((ii+1,j))

(i,j-1)

(i, j – 1)

Рис. 3.15. Шаблон явной схемы для волнового уравнения

Подставив эти выражения в (3.50), получим явную разностную схему:

u j+1	− 2u j + u j−1		j		2	u j	− 2u j + u j		j
i	i	i	= (gi	)		i+1	i	i−1	+ fi	.	(3.53)
	τ 2		= (gi	)			h2		+ fi	.	(3.53)
	τ 2						h2

(i, j + 1)

(i, j+1)

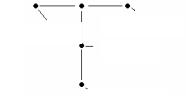
Схеме (3.53) отвечает шаблон типа «крест», изображенный на рис. 3.15. Он иллюстрирует тот факт, что для вычисления значения искомой функции на временном слое j + 1 необходимо знать значения этой функции на двух предыдущих слоях j и j – 1. Следовательно, для того, чтобы начать расчет, необходимо знать значения сеточной функции на первых двух временных слоях.

Решение на временном слое t = t0

(i – 1, j)

(i-1, j)

данными (3.51): u i0 = σ1(xi ). Чтобы вычислить решение при t = t1

воспользуемся формулой Тейлора, а также начальными данными (3.51) и уравнением (3.50):

u(t1, x) = u(t0 , x) +τut (t0 , x) +

= σ1 (x) +τσ 2	(x) + τ	2
			g 2 (t 0 ,
	2

τ 2		utt		(t 0 , x) + τ 3			uttt (t 0 , x) + ... =
2					6
		2
x)	d		σ1(x)			+ f (t0 , x)		+ Cτ 3.

			dx		2

Для нахождения значений сеточной функции uij во внутренних точках xi = ih, i = 1, …, N – 1, на временных слоях tj, j = 2, 3, …, M, используем разностную схему (3.53):

uij+1 = 2uij − uij −1 + r 2 g 2 (uij+1 − 2uij + uij−1 ) + τ 2 fi	j ,
i = 1, 2, …, N – 1.	(3.54)
Для определения искомой сеточной функции	на линиях

x = x0, x = xN воспользуемся краевыми условиями. В случае первой краевой задачи (p1 = 0, s1 = 0) значения функции в гранич-

133

ных точках задаются точно: u 0j = A(t j ), u Nj = B(t j ). Если p1 ¹ 0,

s1 ¹ 0 (вторая или третья краевая задача), производные в (3.52) необходимо заменить конечно-разностными соотношениями. Используем формулы первого порядка аппроксимации:

u j - u j

u j

- u j

p0u0

+ p1

= A

s0uN + s1

N −1

= B

p u j - A j h

B j h + s u j

1 1

, uN

N −1

j = 2, 3, ..., M .

p1 - p0h

hs0 + s1

откуда

(3.55)

Можно показать, что схема (3.54) имеет второй порядок аппроксимации относительно h. Однако соотношения (3.55) имеют лишь первый порядок аппроксимации, что, несомненно, снижает общую точность полученного приближенного решения. Чтобы общий порядок аппроксимации задачи не понижался, для аппроксимации производных в граничных условиях (3.52) необходимо использовать соотношения второго порядка аппроксимации:

- 3u j + 4u j - u j

3u j

- 4u j

+ u j

p0u0

+ p1

= A

s0uN

+ s1

N −1

N −2

= B

откуда легко получить выражения для u0j , uNj , имеющие второй порядок аппроксимации.

Исследование устойчивости разностной схемы

Для того, чтобы решение задачи (3.54) сходилось к решению исходной задачи, требуется устойчивость этой схемы. Опишем один из методов исследования устойчивости. Рассмотрим задачу Коши:

¶2u - g 2 ¶2u = 0, - ¥ < x < ¥,				0 < t < T , g = const,
¶t 2	¶x2	¶u(x,0) =ψ		(3.56)
				(3.56)
u(x,0) =ψ1(x),			2 (x),	- ¥ < x < ¥,
		¶t

которую аппроксимируем разностной схемой

134

umj+1 - 2umj + umj−1		- g 2	umj +1 - 2umj - umj −1		= 0,

τ 2				h2
j = 1, 2, ... , M -1,					(3.57)
um0 =ψ1 (xm ),	u1m - um0			=ψ 2 (xm ), m = 0, ±1, ...
		τ

Для устойчивости разностной схемы относительно возмущения начальных данных необходимо, чтобы решение задачи (3.57) удовлетворяло условию

max	umj	£ C×max	um0	, j = 0,1, ... , M ,	(3.58)
m		m
		m

при произвольной ограниченной функции ψ 1 ( xm ) , в частности, для ψ1 = eiαm , где α – вещественный параметр. Тогда решение задачи (3.56) можно искать в виде

umj = λ j eiαm ,

(3.59)

где λ = λ(α ) . Условие (3.59) выполняется, если числа λ(α ) ле-

жат внутри круга единичного радиуса, т.е.
λ (α ) £ 1.	(3.60)

Неравенство (3.60) выражает необходимое условие устойчивости Неймана. Подставив (3.59) в (3.57), для определения λ (α ) получим уравнение

2		- 2r	2	g	2	sin	2 α		= 0 .	(3.61)
λ	- 2 1	- 2r		g		sin		λ +1	= 0 .	(3.61)
							2

По теореме Виета произведение корней этого уравнения равно 1, т.е. для выполнения условия (3.60) требуется, чтобы корни λ1,2 уравнения (3.61) были комплексно сопряженными и лежали

на единичной окружности. Для этого, в свою очередь, необходимо, чтобы дискриминант D(α ) уравнения (3.51) был отрицателен:

D(α ) º 4r 2 g 2 sin 2 α r 2 g 2	sin 2	α -1		< 0.
2		2

Данное неравенство выполняется при всех α, если gr ≤ 1 . Следовательно, условием устойчивости схемы (3.57) будет

135

(i, j – 1)

Рис. 3.16. Шаблон неявной схемы для волнового уравнения

τ £	h	.	(3.62)

	g

Пусть теперь g = g(x, t) ¹ const. В этом случае применяется принцип «замороженных коэффициентов», в соответствии с которым необходимое условие устойчивости Неймана можно записать в виде

τ £	h	, g* = max g(x, t).	(3.63)
	g*
		x,t

В заключение отметим, что вопрос влияния граничных условий на устойчивость разностной схемы здесь не рассматривается.

Неявная разностная схема

При построении схемы (3.53) производная uxx была заменена на конечную разность на временном слое tj = jτ. Если же использовать значения с временного слоя tj + 1, то получим схему

	uij+1 - 2uij + uij−1	= g j+12
	τ 2	= g j+12
	τ 2	i

которой соответствует шаблон,

Из уравнения (3.64) невозможно явно выразить uij+1

через значения функции u с предыдущих слоев по времени (j и j – 1), поскольку в

(3.61) наряду с uij+1 входят неизвестные uij++11 и uij−+11 . По-

uij++11 - 2uij+1 + uij−+11	+τ 2 f	j+1	, (3.64)
h2
		i

изображенный на рис. 3.16.

(i + 1, j + 1)

(i – 1, j + 1)

(i, j)

этому данная схема называется неявной.

Анализ устойчивости показывает, что неявная схема безусловно устойчива, т.е. обеспечивает сходимость разностной задачи к решению соответствующей дифференциальной при любом отношении τ/h. Решение на первых двух временных слоях определяется из начальных данных так же, как это сделано для явной

схемы. Обозначив γ = gij +12r2 , перепишем (3.64) в виде

136

γu j+1	− (1 + 2γ )u j+1	+ γu j+1	= −2u j + u j−1		+ τ 2 f	j+1,	(3.65)
i+1	i	i−1	i	i	i		(3.65)
i = 1, 2, ..., N −1.

Дополнив (3.65) формулами, аппроксимирующими краевые условия, получим СЛАУ с трехдиагональной матрицей, которая решается с помощью метода прогонки (см. Раздел 1).

Тема 12. Современные пакеты прикладных программ для решения задач строительства*

В настоящее время невозможно представить решение сложных инженерных задач без помощи методов численного моделирования. В каждой из прикладных областей существует иерархия подходов для решения различных проблем, предлагаемых практикой. На их основе разрабатываются как коммерческие, так и свободно распространяемые программы. Так, в строительной области на сегодняшний день завоевывают попу-

лярность пакеты ABAQUS, SCAD, LS-DYNA, ЛИРА, COSMOS,

ANSYS, NEiNASTRAN и др.

Основными схемами, используемыми для расчета работы конструкций в этих программных системах, или САПР (системы автоматизированного проектирования; англ. CAE – Computer Aided Engineering), являются конечно-элементные методы (МКЭ). Их описание приведено в Разделе 2.

Напомним, что метод конечных элементов предназначен для решения дифференциальных уравнений. Конечно-элемент- ный анализ позволяет моделировать нагрузку на конструкцию и определять ее реакцию на эту нагрузку. Конструкция моделируется набором дискретных блоков, которые называются элементами. Число этих блоков конечно, в то время как физическая постановка содержит бесконечное количество элементов. Поэтому естественно, что в результате мы получаем приближенное решение, и очень важно, насколько точно мы определяем искомую реакцию конструкции на нагрузку.

* Авторы выражают благодарность за помощь в подготовке Темы 12 аспирантке кафедры прикладной математики НГАСУ (Сибстрин) С.А. Вальгер.

137

С математической точки зрения суть метода заключается в разбиении области решения на конечное число подобластей (элементов) и построении внутри них аппроксимирующей функции некоторого порядка (базисной функции, функции формы). Значения функции на границах элементов являются решениями исходной задачи. В результате получается система линейных алгебраических уравнений с разреженной матрицей, которая затем решается одним из известных способов.

В данном пособии в качестве основы для получения представлений о современных методах численного моделирования и об использовании программных пакетов расчета задач строительства выбран пакет ANSYS. Данный коммерческий продукт, помимо расчетных возможностей в области строительства и механики твердого тела, включает также линейку программ, предназначенных для решения задач газодинамики, электромагнетизма, теплообмена и микроэлектроники. В каждом из них используется свой набор численных методов. Мы сосредоточимся на задачах строительства и МКЭ. Поскольку интерфейс программы не русифицирован, для удобства читателя названия большинства терминов и объектов будут дублироваться на английском языке.

12.1. Базовые сведения

Современные версии ANSYS предлагают пользователю общую платформу для работы с различными приложениями, имеющимися в пакете. Эта платформа называется ANSYS Workbench; она является средой для разработки инженерных проектов, которые связываются воедино даже в случае междисциплинарных расчетов, включающих разные аспекты одной проблемы (прочность, теплообмен, аэродинамика). Удобный и понятный для инженеров интерфейс платформы позволяет обновлять данные на уровне проекта, проводить параметрические и оптимизационные расчеты, обеспечивает связь с САПР системами. Таким образом, многие приложения, ранее являвшиеся независимыми, были интегрированы в среду Workbench. Мо-

138

дуль для расчета прочности и устойчивости конструкций носит название ANSYS Mechanical и доступен как в виде самостоятельного приложения, так и в составе Workbench. Выполнение сложных прочностных и многодисциплинарных расчетов доступно пока лишь в традиционном интерфейсе ANSYS и носит название Mechanical APDL. APDL (ANSYS Parametric Design Language) – это язык, созданный для написания программ, скриптов, пользовательских окон данного решателя.

Всреде Mechanical возможно проведение следующих типов расчетов конструкций на прочность:

1. Статический (или переходный к динамическому) анализ (Static Analysis) определяет деформации, напряжения и т.п. при статических нагрузках. Сюда включаются как линейные, так и нелинейные постановки. Нелинейность может включать явления пластичности, больших деформаций, упрочнения, ползучести, поверхности контакта и т.п.

2. Динамический анализ (Transient Dynamic Analysis) ис-

пользуется для определения отклика конструкции на произвольные нагрузки, изменяющиеся во времени. Все нелинейности, рассматриваемые в статическом анализе, также могут быть учтены.

3. Модальный анализ (Modal Analysis) рассчитывает естественные частоты и формы колебаний конструкции. Имеет дополнение в виде спектрального анализа (Spectrum Analysis).

4. Гармонический анализ (Harmonic Analysis) призван определять отклик конструкции при воздействии нагрузок, зависящих от времени по гармоническому закону.

5. Расчет потери устойчивости (Buckling Analysis).

6. Оптимизация формы.

7. Расчет контактных задач: скольжение с разделением, трение, уплотнение.

Вдополнение к прочностным расчетам имеется возможность провести (отдельно или совместно, т.е. с учетом взаимовлияния) тепловой расчет (Thermal) – стационарный и неста-

139

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 1314 / 1614 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.04.2015125.95 Кб35Планировка и застройка микрорайона ГСХ ГОС-2.doc
#
03.08.201922.88 Mб10ПОВЕРХНОСТИ.docx
#
15.07.20194.52 Mб4Подготовка геодезических данных для перенесения....rtf
#
16.09.201965.54 Кб4Портфолио-практика.doc
#
09.04.20152.58 Mб34Пособие к СНиП II-23-81.pdf
#
09.04.20151.64 Mб92Пособие_Бедарев_Федорова_Федорченко.pdf
#
09.04.201542.36 Кб167Постоянный электрический ток.docx
#
04.05.2015690.03 Кб41Пояснилка ТСП Влад.docx
#
14.03.2016787.41 Кб93Пояснилка ТСП Влад.docx
#
16.11.2019126.53 Кб5Пояснит записка.docx
#
14.03.20161.98 Mб87право ответы к экз 200 стр.docx