Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Новосибирский государственный архитектурно-строительный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Пособие_Бедарев_Федорова_Федорченко

.pdf

Скачиваний:

Добавлен:

09.04.2015

Размер:

1.64 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1611 12 13 14 15 16 > Следующая >>>

unj +1 - unj

	n +1	n +1			n +1
σ	u j +1	- 2u j		+ u j −1		+
σ		h2				+
= A		h2		n		n	+ F (x j , t n ) , (3.14)
		n		n		n
	-σ )	u j +1 - 2u j			+ u j −1
(1	-σ )		h2

где 1 ³ σ ³ 0 – параметр, который можно подбирать для того, чтобы добиться улучшения аппроксимации или устойчивости схемы. При σ = 0 (3.14) переходит в явную схему (3.9), а при

σ= 1 – в чисто неявную схему (3.13). При всех других значениях

σв каждом разностном уравнении будут завязаны значения неизвестной функции в шести разных точках, в отличие от явной и неявной схем, в которых завязаны четыре различные точки.

Графическое представление точек расчетной области, входящих в разностное уравнение, называется шаблоном конечно-

разностной схемы. Шаблоны схем (3.9), (3.13) и (3.14) при σ ¹ 0 представлены на рис. 3.3а– в соответственно. В зависимости от того, сколько временных слоев входит в шаблон, схемы бывают

двухслойными или трехслойными. Рисунок 3.3 показывает, что все схемы семейства (3.14) являются двухслойными. Реализация схемы зависит от того, сколько точек находится на верхнем слое шаблона, представляющем искомые величины. Если число точек на верхнем слое меньше или равно двум, решение можно найти с помощью явной процедуры. Схемы, шаблон которых имеет на верхнем слое три точки, реализуются с помощью точного экономичного метода прогонки (см. Раздел 1). Если же на верхнем слое больше трех точек, необходимо применять метод решения СЛАУ с заполненной матрицей, что приводит к существенному увеличению времени расчета.

Для схемы (3.13) на каждом временном шаге необходимо решить СЛАУ с трехдиагональной матрицей:

un0 = μ11(tn),

γu nj −+11 − (1 + 2γ )unj +1 + γu nj ++11 = u nj + τ F (x j , t n ) , i = 1, 2, …, N – 1. (3.15) unM = μ12(tn).

100

	a			б			в
		t = t n +1			t = t n+1			t = t n+1
		t = t n			t = t n			t = t n
x = xj– 1 x = xj x = xj+1			x = xj– 1 x = xj x = xj+1			x = xj– 1 x = xj x = xj+1

Рис. 3.3. Шаблоны разностных схем (3.9), (3.13) и (3.14)

Решение системы (3.15) находится с помощью прогонки. Для случаев второй и третьей краевой задачи изменяются первое уравнение (3.15), из которого определяются значения первых прогоночных коэффициентов, и последнее уравнение, из которого на обратном этапе прогонки определяется решение в последнем узле сетки. В случае использования более общей схемы (3.14) изменится правая часть уравнений (3.15), однако СЛАУ останется трехдиагональной.

Как было отмечено выше, за счет выбора параметра σ можно добиться, чтобы схема имела более высокий порядок аппроксимации. В частности, легко показать, что симметричная схема (σ = 0.5) будет иметь порядок аппроксимации τ2 + h2. Кроме то-

го, при специальном выборе весового параметра σ =	1	-		h2
			12Aτ
2

можно добиться, чтобы схема имела порядок аппроксимации

τ2 + h4 .
	Схема			(3.14) устойчива при выполнении условия
σ ³	1	-	h2	, откуда, в частности, легко показать, что неявная
			4 A2τ
2

(σ = 1), симметричная (σ = 0.5) схемы и схема повышенного по-

рядка аппроксимации σ

1h2

=- абсолютно устойчивы.

212 Aτ

Нахождение решения разностной схемы (3.14) при σ ¹ 0 аналогично случаю чисто неявной схемы. Система трехточечных уравнений, связывающих решение в точках верхнего (n + 1)-го слоя, имеет вид:

101

n+1		n+1	n+1		n		unj+1 - 2unj		+ uтj−1
σγu j−1	- (1 +	2σγ )u j	+ γσu j+1	= u j		+τ (1-σ )				+
							h	2

+τF (x j , t т ),		n = 0,1, ..., M -1,			j = 1, 2,¼, N -1,

который отличается от (3.15) только правой частью и, следовательно, также решается методом прогонки.

По аналогии с двухслойными схемами (3.15), для уравнения (3.6) можно построить семейство трехслойных схем. Обозначим

n		unj +1 - 2unj + unj −1			h2		IV		4
Lu j	= A		= uxx	+		u		+ O(h		) .
Lu j	= A	h2	= uxx	+	12	u		+ O(h		) .
		h2			12

Тогда семейство трехслойных схем можно записать в виде

unj	+1 - u nj	−1
			= L(σu nj +1	+ (1 - 2σ )u nj + σu nj −1 ).	(3.16)
	2τ		= L(σu nj +1	+ (1 - 2σ )u nj + σu nj −1 ).	(3.16)
	2τ

При любых σ схема (3.16) аппроксимирует уравнение (3.6) с порядком O(τ2 + h2), а устойчивость имеет место при σ > 0.25. При любом σ ¹ 0 шаблон схемы будет иметь три точки на верхнем (неявном) слое, что обусловливает необходимость использования метода прогонки.

Чтобы начать расчеты по трехслойной схеме, нужно знать решение на первых двух временных слоях: t0, t1. Однако из начальных данных известно решение только на слое t0. Есть два способа реализации схемы:

1. Решение на первом временном слое находится из разложения в ряд Тейлора с учетом исходного уравнения.

u1j = u0j		+ τut + τ 2 utt + O(τ 3 ),
		2
ut = A2uxx º Lu, utt = (Lu)t = L(ut ) = L2u,
1	0	0	τ 2	2 0	τ 2 2	).
u j	= u j	+ τLu j +	L u j = (E + τL +		L )ϕ(x j	).
			2		2

2. Зная начальные данные (т.е. решение на «нулевом слое»), находим решение на первом временном слое по какой-либо двухслойной схеме (явной, неявной). Далее используем трехслойную схему.

102

9.2. Двумерное уравнение теплопроводности

Рассмотрим теперь конечно-разностные схемы для двумерной задачи. Пусть G = [0, Lx] ´ [0, Ly] – прямоугольная область на плоскости (x, y), ¶G – граница области G, u(x, y, t) – функция, определенная в области G ´ [0, T]. Рассмотрим задачу нахождения решения u(x, y, t), удовлетворяющего уравнению

¶u		¶2 u		+	¶2 u		+ F ( x, y,t),	(3.17)
	= A		2			2
¶t		¶x			¶y

дополненному начальными данными

u(x, y, 0) = u0(x, y)

и краевыми условиями первого рода

u(x, y, t)½∂G = μ(t).

Введем в области G ´ [0, T] конечно-разностную сетку с

шагами hx = Lx/Nx, hy = Ly/Ny и τ = Т/М: tn = n · τ, xi = ihx, yj = jhy,

где Nx, Ny – количество разбиений области по осям x и y. Построим семейство двухслойных конечно-разностных схем:

uijn+1 - uijn

+A(1 -σ

+F (xi , y

un +1

- 2un +1

+ un+1

i +1 j

i −1 j

= Aσ

un+1

- 2un +1

+ un+1

ij +1

ij −1

ui +1 j

2uij

+ ui −1 j

uij +1 - 2uij

+ uij −1

(3.18)

)

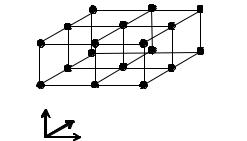
j , t n ).

Шаблон схемы (3.18), представленный на рис. 3.4, включает 9 точек на неизвестном, (n + 1)-м временном слое, и 9 точек на известном n-м слое.

103

y = yj+1	t = t	n+1
	t = t

y = yj

y = yj– 1

t = tn

x = xi– 1	x = xi	x = xi+1
t	y
	y
	x

Рис. 3.4. Шаблон схемы (3.18) для уравнения (3.17)

При σ = 0 схема является явной, и ее решение можно найти по формулам:

n+1			n	n	n		n	n	n
n+1	n	ui+1 j		- 2uij	+ ui−1 j		uij +1	- 2uij	+ uij−1
uij	= uij	+τA				+				+
uij	= uij	+τA		2		+		2		+
				2				2
				hx				hy

+ F (xi , y j , t n ), i = 1, 2, ..., N x ; j = 1, 2, ..., N y ; n = 0,1, 2, ..., M -1.

Явная схема имеет порядок аппроксимации О(τ + hx2 + hy2). Как и в случае одной пространственной переменной, схема является условно устойчивой. Для того, чтобы получить устойчивое приближенное решение, шаги разностной сетки должны удовлетворять условию Куранта:

	τ		τ	£	1
A h2		+ h2		£	2 .
x			y

Свойством безусловной устойчивости схема будет обладать при

σ >	1	-	h2	, h = max(hx , hy ).
			4τA
2

При σ ¹ 0 шаблон схемы (3.18) будет включать 9 точек на верхнем временном слое. Для нахождения решения на неизвестном (n + 1)-м слое необходимо решить СЛАУ с заполненной матрицей, для которой экономичный метод прогонки неприменим, что делает процесс решения весьма трудоемким. В этом случае используются так называемые методы дробных шагов, в

104

которых процесс нахождения решения на новом, (n + 1)-м временном слое разбивается на несколько промежуточных (дробных) шагов. Таким образом, на каждом шаге по одному из пространственных направлений схема является явной, а по другому – неявной. Неявность схемы по выбранному направлению делает ее безусловно устойчивой. В то же время для нахождения решения на новом временном слое не требуется решать СЛАУ с заполненной матрицей, а можно найти решение с помощью нескольких прогонок. Эта методика широко используется при решении многомерных уравнений.

Существует много различных схем в дробных шагах для уравнения теплопроводности. Наиболее распространенной явля-

ется схема продольно-поперечной прогонки:

n +

− 2u

2 + u

n +

i +1 j

i −1 j

uij

− uij

hx2

+ F (x , y ,t

);

= A

τ / 2

+ uijn+1 − 2uijn + uijn−1

(3.19)

n +

2 − 2u

+ u

n 1

i +1 j

−1 j

uij

− uij 2

hx2

+ F (x , y

n +

= A

, t

τ / 2

n +1

+ uij +1

− 2uij

+ uij −1

Запишем схему в операторном виде:

	τ
E −	2
	2
	τ
E −	2
	2

Λ1			n + 1
Λ1		uij

Λ	2	un +1
	2		ij

2 =

F (xi , y j

, t

E +

uij

E +

n +

F (x , y

, t

где	Λ un = A	uin+1, j − 2uin, j + uin+1, j	, Λ	un = A	uin, j −1 − 2uin, j + uin, j +1	,
где	Λ un = A		, Λ	un = A		,
	1 ij	h2	2	ij	h2
		h2			h2
		x			yx

Е – тождественный оператор. Чтобы исследовать аппроксима-

105

цию схемы, нужно исключить из нее дробный шаг u									n+ 1
цию схемы, нужно исключить из нее дробный шаг u									2 . При-
меним операторы		τ	Λ1			τ	Λ1	к первому и второму
меним операторы	E −		Λ1	,	E +		Λ1	к первому и второму
		2				2

уравнениям (3.19), соответственно выразим из уравнений член

E − τ		Λ	1	E + τ		Λ	1	u n+1/ 2	и приравняем правые части. Таким
	2		1		2		1	ij
	2				2
образом, получим схему в «целых шагах»:

un +1

− un

un + un +1

F n + F n +1

= (Λ + Λ )

−

n +1

−

Λ Λ

uij

− uij

откуда следует, что схема (3.19) аппроксимирует уравнение (3.17) с порядком О(τ2 + h2). Схема безусловно устойчива и экономична.

Реализация схемы проводится следующим образом. Пусть решение на n-м временном слое известно. Из первого разностного уравнения с помощью метода прогонки по направлению x находится решение на (n + ½)-м шаге. Затем из второго уравнения также с помощью прогонки по направлению y определяется решение на (n + 1)-м временном слое. Недостатком схемы является то, что она не обобщается на трехмерный случай.

В случае ненулевых краевых условий или правых частей, граничные условия на дробном шаге необходимо задавать специальным образом. Для этого в обоих уравнениях (3.19) перене-

сем слагаемые, содержащие uijn+ 12 , в левую часть:

Λ1

n + 1

F (xi , y j , t

E −

uij

E +

uij

E +

n + 1

E −

n 1

−

F (x , y

, t

n 1

Сложив эти уравнения, получим

106

n+ 1

uijn + uijn+1

uijn − uijn+1

−

(F n − F n+1 )

Последнее равенство позволяет определить решение на

дробном

шаге

на

вертикальных

границах:

i = 0 и i = Nx,

j = 1, 2, …,

Ny.

Для решения (3.17) используют также схему расщепления:

2 − u n

2 − 2u

2 + u

= A

i+1 j

−1 j

+ F (x , y

, t n+1 ),

hx2

(3.20)

n+1

uij

− uij

uij+1

−

2uij

+ uij−1

;

и схему предиктор –

корректор:

n +

uij

4 − uij

= Λ un +

+ F (x , y , t n +

2 ),

τ / 2

1 ij

n +

uij

2 − uij

= Λ

n +

(3.21)

2uij

2 ,

τ / 2

un +1 − u n

n +

= (Λ + Λ

2 + F (x , y , t 2 ).

Исследование аппроксимации для этих схем проводится так же, как и для (3.19). Преимуществом схем (3.20), (3.21) по сравнению с (3.19) является то, что они могут быть легко обобщены на пространственный случай.

Тема 10. Уравнение Пуассона

В качестве классического представителя уравнений эллиптического типа рассмотрим двумерное уравнение Пуассона:

u ≡	∂2u +	∂2u = F (x, y) ,	(3.22)
	∂x2	∂y2
	107

F(x, y) – функция источников. Уравнение Пуассона описывает, например, распределение электростатического поля или стационарное распределение температуры. Частным случаем этого уравнения является уравнение Лапласа u = 0 .

Пусть требуется определить решение в некоторой области G на плоскости (x, y). Корректная постановка задачи требует задания граничных условий на границе этой области ∂G .

В одномерном случае уравнение Пуассона не что иное, как краевая задача первого рода для ОДУ второго порядка, решение которой было рассмотрено в Теме 7.

10.1. Метод установления

Сравнивая уравнение Пуассона и рассмотренное выше двумерное уравнение теплопроводности, можно понять, что уравнение Пуассона является стационарным, т.е. не зависящим от времени вариантом уравнения теплопроводности. Поэтому для решения уравнения Пуассона часто используют так называемый метод установления. Для этого в правую часть уравнения (3.22)

добавляют слагаемое ∂u и решают полученное уравнение теп-

∂t

лопроводности с помощью описанных в Теме 9 методов до тех пор, пока решение не выйдет на стационар, т.е. не перестанет изменяться в зависимости от времени. Время в этой задаче является фиктивным, и в разностных схемах надо использовать максимально возможный шаг. Решение нестационарной задачи стремится к решению стационарной независимо от выбора начальных данных. Процесс установления решения может занять продолжительное время, особенно если используются явные схемы, имеющие жесткое ограничение на временной шаг. В этом случае применение схем дробных шагов помогает существенно сократить время решения.

10.2. Итерационные методы

Для решения уравнения Пуассона используются и другие методы, не связанные со сведением его к уравнению теплопроводности. Как правило, все эти методы приводят к решению

108

СЛАУ с заполненной матрицей, которая решается одним из итерационных методов.

Пусть	областью G = {a £ x £ b, c £ y £ d } будет	прямо-
угольник,	на границах которого задано гладкое	решение

u(x, y)½∂G = γ. Построим в области G прямоугольную расчетную

сетку с шагами hx =

b - a

, hy

d - c

. Аппроксимируя вторые

N x

N y

производные центральными разностями, имеем:

uij−1 - 2uij + uij+1

uij −1 - 2uij + uij +1

= F j ,

i =1, ..., Nx -1,

j =1, ..., N y -1 ,

u j

= γ j

, u j

= γ j , u0

= γ i

, u N y

= γ i .

N x

Для прямоугольной области полученную систему линейных алгебраических уравнений можно записать в векторно-матрич- ной форме:

	0

A = 0
i	...
	...
	0
	0

Bi	= 0
	...

	0

		R				R				R		= Fi
Aiui−1				- Ciui				+ Biui+1				= Fi	,						(3.23)
0 ...			0						1			2(h2	0			0			... 0
h2 ...			0					- h2				2(h2	+ h2 )		- h			2	... 0
y			, C =							x		x	y					x	,
... ...			...		i			...				...			...				... 0
... ...			...					...				...			...				... 0
0 ...			0						0				0			0			... 1
0 ...			0					ui0					γ 3i
h2 ...			0		R			u1				R	f 1
x				,	ui	=			i		,	Fi = hx2 hy2			i		,
... ...			...					...					...
0 ...									N y						i
0 ...			0			R		ui					γ 4
R			= γ		j ,	R			= γ j		,	j =1, ..., N			.
u	0		= γ		j ,	u	N x		= γ j		,	j =1, ..., N		y	.
	0			1			N x			2				y

Система (3.23) имеет блочно-трехдиагональную матрицу и может быть решена с помощью метода матричной прогонки. Однако этот метод требует больших затрат машинного времени и практически не применяется. Для решения (3.23) обычно используют итерационные методы. Достаточно эффективным

109

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1611 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.04.2015125.95 Кб35Планировка и застройка микрорайона ГСХ ГОС-2.doc
#
03.08.201922.88 Mб10ПОВЕРХНОСТИ.docx
#
15.07.20194.52 Mб4Подготовка геодезических данных для перенесения....rtf
#
16.09.201965.54 Кб4Портфолио-практика.doc
#
09.04.20152.58 Mб34Пособие к СНиП II-23-81.pdf
#
09.04.20151.64 Mб92Пособие_Бедарев_Федорова_Федорченко.pdf
#
09.04.201542.36 Кб167Постоянный электрический ток.docx
#
04.05.2015690.03 Кб41Пояснилка ТСП Влад.docx
#
14.03.2016787.41 Кб93Пояснилка ТСП Влад.docx
#
16.11.2019126.53 Кб5Пояснит записка.docx
#
14.03.20161.98 Mб87право ответы к экз 200 стр.docx