
- •Федеральное агентство по образованию
- •2404000000-35 Удк 681.142:519.6
- •Оглавление
- •1. Основы работы в Mathcad 10
- •2. Роль численных методов 36
- •3. Методы аппроксимации и интерполирования 42
- •4. Лабораторная работа № 1. Интерполирование степенными многочленами 44
- •5. Лабораторная работа № 2. Параметрическая идентификация математических моделей методами аппроксимации 65
- •6. Решение систем линейных алгебраических уравнений 93
- •7. Лабораторная работа № 3. Решение систем линейных уравнений приближенными методами 109
- •8. Лабораторная работа № 4. Решение нелинейных уравнений приближенными методами 142
- •9. Лабораторная работа № 5. Решение систем нелинейных уравнений приближенными методами 174
- •10. Лабораторная работа № 6. Решение обыкновенных дифференциальных уравнений первого порядка численными методами 197
- •11. Лабораторная работа № 7. Численное интегрирование 212
- •12. Лабораторная работа № 8. Моделирование реактора идеального вытеснения для многостадийной химической реакции с линейной кинетикой 226
- •13. Лабораторная работа № 9. Расчет моделей процессов диффузии и теплопроводности с помощью явной разностной схемы 249
- •Предисловие
- •1. Основы работы в Mathcad
- •1.1. Панели инструментов
- •1.2. Ввод и вывод данных
- •1.3. Осуществление несложных вычислений
- •1.4. Построение и настройка графиков
- •1.5. Программирование в Mathcad
- •1.5.1. Программирование без программирования
- •1.5.2. Язык программирования Mathcad
- •1.5.3. Создание программы (Add Line)
- •1.5.4. Редактирование программы
- •1.5.5. Локальное присваивание ()
- •1.5.6. Условные операторы (if, otherwise)
- •1.5.7. Операторы цикла (for, while, break, continue)
- •1.5.8. Возврат значения (return)
- •1.5.9. Перехват ошибок (on error)
- •1.5.10. Примеры программирования
- •2. Роль численных методов
- •2.1. Этапы решения задачи на компьютере
- •2.2. Математические модели
- •2.3. Численные методы
- •3. Методы аппроксимации и интерполирования
- •4. Лабораторная работа № 1. Интерполирование степенными многочленами
- •4.1. Постановка задачи
- •4.2. Порядок выполнения работы
- •4.3. Краткие теоретические сведения
- •4.3.1. Метод неопределенных коэффициентов
- •4.3.2. Интерполяционный многочлен Лагранжа
- •4.3.3. Интерполяционные формулы Ньютона для равностоящих узлов
- •4.4. Примеры выполнения
- •4.4.1. Интерполирование степенными многочленами с использованием метода неопределенных коэффициентов
- •4.4.2. Интерполирование степенными многочленами с использованием второй интерполяционной формулы Ньютона
- •4.5. Требования к отчету
- •4.6. Контрольные вопросы и задания
- •4.7. Задания
- •5. Лабораторная работа № 2. Параметрическая идентификация математических моделей методами аппроксимации
- •5.1. Постановка задачи
- •5.2. Порядок выполнения работы
- •5.3. Краткие теоретические сведения
- •5.3.1. Метод выбранных точек
- •5.3.2. Метод средних
- •5.3.3. Метод наименьших квадратов
- •5.4. Примеры выполнения
- •5.4.1. Аппроксимация с использованием метода выбранных точек
- •5.4.2. Аппроксимация с использованием метода средних
- •5.4.3. Аппроксимация с использованием метода наименьших квадратов
- •5.4.4. Сравнительный анализ методов аппроксимации
- •5.5. Требования к отчету
- •5.6. Контрольные вопросы и задания
- •5.7. Задания
- •6. Решение систем линейных алгебраических уравнений
- •6.1. Общие положения
- •6.2. Точные методы решения систем линейных уравнений
- •6.2.1. Метод Крамера
- •6.2.2. Метод Гаусса
- •6.2.3. Метод обращения матриц
- •7. Лабораторная работа № 3. Решение систем линейных уравнений приближенными методами
- •7.1. Постановка задачи
- •7.2. Порядок выполнения работы
- •7.3. Краткие теоретические сведения
- •7.3.1. Математическое описание реактора идеального смешения непрерывного действия
- •7.3.2. Математическое описание кинетических закономерностей химических превращений
- •7.3.4. Приближенные методы решения систем линейных уравнений
- •7.3.4.1. Метод простых итераций
- •7.3.4.2. Метод Зейделя
- •7.4. Примеры выполнения
- •7.4.1. Пример выполнения задания точным методом
- •7.4.2. Пример выполнения задания методом итераций и методом Зейделя
- •7.5. Требования к отчету
- •7.6. Контрольные вопросы и задания
- •7.7. Задания
- •8. Лабораторная работа № 4. Решение нелинейных уравнений приближенными методами
- •8.1. Постановка задачи
- •8.2. Порядок выполнения работы
- •8.3. Краткие теоретические сведения
- •8.3.1. Этапы решения нелинейного уравнения
- •8.3.4. Метод деления отрезка пополам (вилки, дихотомии)
- •8.3.5. Метод Ньютона (метод касательных)
- •8.3.6. Метод простых итераций
- •8.4. Пример выполнения задания методом итераций
- •8.5. Требования к отчету
- •8.6. Контрольные вопросы и задания
- •8.7. Задания
- •9. Лабораторная работа № 5. Решение систем нелинейных уравнений приближенными методами
- •9.1. Постановка задачи
- •9.2. Порядок выполнения работы
- •9.3. Краткие теоретические сведения
- •9.3.1. Метод Ньютона
- •9.3.2. Метод итераций
- •9.4. Примеры выполнения
- •9.4.1. Метод Ньютона
- •9.4.2. Метод итераций
- •9.5. Требования к отчету
- •9.6. Контрольные вопросы и задания
- •9.7. Задания
- •10. Лабораторная работа № 6. Решение обыкновенных дифференциальных уравнений первого порядка численными методами
- •10. 1. Постановка задачи
- •10.2. Порядок выполнения работы
- •10.3. Краткие теоретические сведения
- •10.3.1. Метод Эйлера
- •10.3.2. Модифицированный метод Эйлера
- •10.3.3. Метод Эйлера-Коши
- •10.3.4. Метод Рунге-Кутта 4-го порядка
- •10.4. Примеры выполнения
- •10.4.1. Реализация метода Эйлера в математическом редактореMathcad
- •10.4.2. Решение обыкновенного дифференциального уравнения 1-го порядка с помощью функции rkfixed
- •10.5. Требования к отчету
- •10.6. Контрольные вопросы и задания
- •10.7. Задания
- •11. Лабораторная работа № 7. Численное интегрирование
- •11. 1. Постановка задачи
- •11.2. Порядок выполнения работы
- •11.3. Краткие теоретические сведения
- •11.3. 1. Метод прямоугольников
- •11.3.2. Метод трапеций
- •11.4. Пример выполнения
- •11.5. Требования к отчету
- •11.6. Контрольные задания
- •1 Таблица 101.7. Задания
- •12. Лабораторная работа № 8. Моделирование реактора идеального вытеснения для многостадийной химической реакции с линейной кинетикой
- •12. 1. Постановка задачи
- •12.2. Порядок выполнения работы
- •12.3. Краткие теоретические сведения
- •12.3.1. Математическая модель реактора идеального вытеснения
- •12.3.2. Численное решение систем дифференциальных уравнений
- •12.4. Пример выполнения
- •12.5. Проверка расчета с помощью функции rkfixed
- •12.6. Требования к отчету
- •12.7. Контрольные вопросы и задания
- •1 Таблица 112.8. Задания
- •13. Лабораторная работа № 9. Расчет моделей процессов диффузии и теплопроводности с помощью явной разностной схемы
- •13.3.2. Решение уравнений в частных производных
- •13.3.3.Метод сетки
- •13.3.4. Явная разностная схема
- •13.3.5. Условия устойчивости явной разностной схемы
- •13.4. Пример выполнения
- •13.5. Требования к отчету
- •13.6. Контрольные вопросы и задания
- •13.7. Задания
- •Библиографический список
- •Использование
13.3.3.Метод сетки
Численные методы решения наиболее полно разработаны для дифференциальных уравнений с двумя и тремя независимыми переменными. Мы ограничимся рассмотрением численных методов с двумя независимыми переменными.
Уравнения (161)–(163) должны быть дополнены соответствующими начальными и граничными условиями, т. е. должно быть заданно значение функции u в момент времени t = t0, а также на концах координаты х.
Такая совокупность
начальных
![]() и граничных
и граничных![]() условий получила название краевых
условий.
условий получила название краевых
условий.
Уравнения подобного типа решаются с помощью метода конечных разностей, сущность которого состоит в том, что за искомый набор чисел принимается таблица значений решения в точках некоторого множества, называемых обычно сеткой.
Для вычисления искомой таблицы используются алгебраические уравнения, приближенно заменяющие исходное дифференциальные уравнение.
Рассмотрим решение дифференциальных уравнений в частых производных на примере диффузионной модели неподвижной среды (модели диффузии вещества в растворителе), которая имеет следующий вид:
![]() (165)
(165)
с начальными и граничными условиями
![]() .
.
Решить уравнение (165) – значит найти распределение концентрации во времени и пространстве (вдоль координат tих), т. е., по сути, построить трехмерный график, который обычно имеет вид криволинейного пространства.
Суть метода сетки заключается в том, что вся заданная пространственно-временная область разбивается на равные интервалы времени и пространства через выбранные интервалы дискретизации t их, и затем по представленной ниже методике находятся значения интересующего нас параметра в каждом узле сетки.
Пусть необходимо найти распределение концентрации С(t,x) на интервале [0,tk], [0,L].Тогда количество интервалов дискретизации по времени будет равно
![]() , (166)
, (166)
а по пространственной координате
![]() . (167)
. (167)
Примем обозначение текущей концентрации в произвольном узле сетки:
по времени верхним индексом (n);
по пространственной координате нижним индексом (k).
Таким образом, необходимо
найти Ckn, т. е.
заполнить сетку при![]() и
и![]() (рис. 103).
(рис. 103).
Р ис.
103. Сетка
ис.
103. Сетка
Для того чтобы решить поставленную задачу, необходимо представить исходное дифференциальное уравнение в виде конечно-разностных отношений.
Существуют следующие способы представления производных в конечно-разностном виде:
1) левое конечно-разностное отношение
![]() ; (168)
; (168)
2) правое конечно-разностное отношение
![]() ; (169)
; (169)
3) центрированное конечно-разностное отношение
![]() . (170)
. (170)
Для решения дифференциального уравнения в частных производных составляется явная разностная схема.
13.3.4. Явная разностная схема
Рассмотрим исходное уравнение (165) в n-й момент времени вk-ой точке пространства. Тогда правая часть уравнения (165) – первая частная производная по времени будет представлена так:
![]() . (171)
. (171)
Поскольку производная по времени, поэтому изменяется индекс n.
Вторая частная производная в сеточной области определяется как отношение разности 1-х производных по длине шага сетки.
 . (172)
. (172)
С помощью этих равенств
производная
![]() с 1-м порядком точности относительно
шагаDtи частная производная
с 1-м порядком точности относительно
шагаDtи частная производная![]() со 2-м порядком точности относительно
шагаDxаппроксимируется в конечно-разностные
отношения.
со 2-м порядком точности относительно
шагаDxаппроксимируется в конечно-разностные
отношения.
Производим замену в уравнении (165).
 . (173)
. (173)
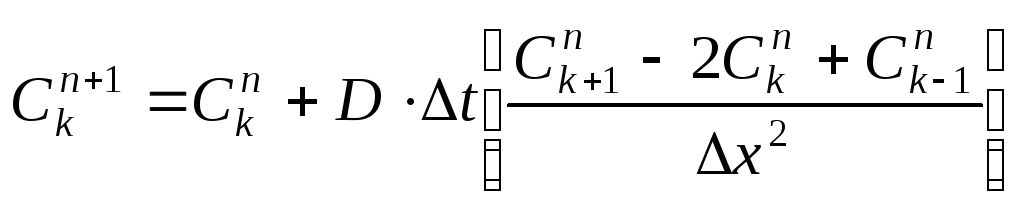 . (174)
. (174)
Из (174) видно, что по значению функции c(x, t)в точкахn-го временного слоя можно вычислить значение функцииc(x, t)в точкахn+1 временного слоя, т. е. мы имеем явную схему (рис. 104).
Р ис.
104. Явная схема
ис.
104. Явная схема
Значение c(x,
t)приt=0определяется из начальных условий:![]() для
для![]() (нижняя граница сетки).
(нижняя граница сетки).
Значение функции с(x, t)в крайних узлах прих=0 их=Lопределяется из краевых условий:
1.
![]() для
для![]() (левая граница сетки).
(левая граница сетки).
2. Для расчета концентраций в сеточной области также необходимо знать CKn– концентрацию на границе (L) (концентрацию на парвом конце сетки), которая вычисляется из граничного условия:
![]() ,
,
откуда следует, что
![]()
![]() .
.
Последовательно
вычисляя С(xк,t1)
для![]() ,
затемC(xк,t2)
для
,
затемC(xк,t2)
для![]() и т. д. доC(xк,tN)
получим профиль концентраций в
произвольный момент времени в произвольной
точке пространства.
и т. д. доC(xк,tN)
получим профиль концентраций в
произвольный момент времени в произвольной
точке пространства.
Таким образом, уравнение
(174) представляет собой систему уравнений,
которая рассчитывается
![]() раз:
раз:
 (175)
(175)

