7.3.4. Приближенные методы решения систем линейных уравнений

7.3.4.1. Метод простых итераций

Допустим, имеется система линейных алгебраических уравнений:

.

При решении этой системы точным методом корень получают сразу (x_точн,y_точнна рис. 44). При подстановке корня в исходную систему получают тождество.

К приближенным методам относятся итерационные методы решения систем. При решении системы приближенным методом корень получают поэтапно, путем повторения ряда действий (итераций).

Итерационнымпроцессом называется повторяющийся процесс вычислений искомой величины по её значению на предыдущем шаге.

Сначала задают начальное приближение (x₀,y₀), затем через эти значения находят следующую точку приближения к решению (x₁,y₁), через неё (x₂,y₂) и т. д. При подстановке полученного корня (x*,y*) в исходную систему получают приближенное равенство.

Рис. 44. Приближенное решение

Для построения итерационных процессов решения линейных систем уравнений последние надо приводить к нормальному виду.

Вид называется каноническим видом, вид– нормальным.

Если в правую часть системы, записанной в нормальном виде, подставить какое-либо значение вектора , то при известных значениях матрицLиможно подсчитать новое значение, подставить его снова в правую часть системы и т. д.

Полученную последовательность векторов , ,называютитерационной последовательностью.

Если последовательность сходится, т. е. имеет предел, то этот предел будет решением исходной системы уравнений.

Для организации приближенного вычисления корней системы линейных уравнений необходимо выполнить следующие действия:

1. привести систему к нормальному виду;

2. определить условие сходимости последовательности по коэффициентам системы, приведенной к нормальному виду;

3. построить итерационный процесс;

4. определить достижение заданной степени точности решения, т. к. точное решение может быть получено при бесконечном итерационном процессе.

Рассмотрим систему линейных уравнений 3-го порядка:

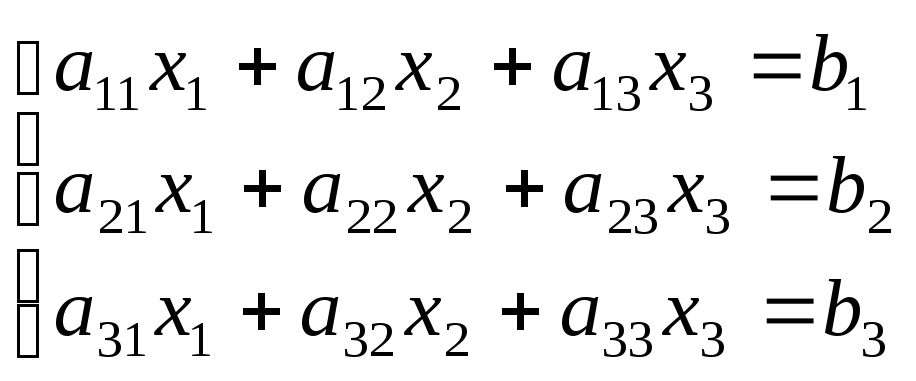(43)

Нормальный вид системы (43):

(44)

Существует бесконечное множество способов приведения системы (43) к виду (44). Среди них всегда найдется такой, при котором будет выполняться условие сходимости итерационной последовательности , ,к соответствующему пределу.

Рассмотрим возможные варианты вычислений _ijи_iна конкретном примере:

(45)

Вариант 1. Представим систему (45) в следующем виде:

или

где

Вариант 2. Для приведения системы к нормальному виду все члены левой части первого уравнения, кроме члена, содержащего а₁₁, перенесем в правую часть и разделим уравнение на а₁₁. Для второго уравнения все члены левой части перенесем также в правую часть, кроме члена, содержащего а₂₂, и разделим уравнение на а₂₂. Для третьего уравнения все члены левой части перенесем в правую часть, кроме члена, содержащего а₃₃, и разделим уравнение на а₃₃. Приведенная система будет иметь вид:

(46)

где

Условием сходимости последовательности к пределу является выполнение следующего требования:

для всех

или (47)

для всех

то есть необходимо, чтобы сумма модулей коэффициентов нормальной системы уравнений по строкам или столбцам была меньше 1.

Для построения итерационной процедуры необходимо выбрать первоначальное значение x₁⁽⁰⁾, x₂⁽⁰⁾, .Рекомендуется в качестве этих значений выбирать либо 0, либо значения свободных членов.

Формульная запись метода простых итераций имеет вид:

,(48)

В приближенных методах задается степень точности получения решения (рис. 44).

Условием достижения заданной степени точности является выполнение следующего неравенства:

. (49)

Поскольку точное решение нам неизвестно, то воспользоваться условием (49) практически невозможно. На практике можно использовать другое условие, эквивалентное (49):

. (50)

Таким образом, условием нахождения вектора неизвестных является выполнение условия:

для всех