6. Решение систем линейных алгебраических уравнений

6.1. Общие положения

Системой mлинейных алгебраических уравнений сnпеременными (линейной системой) называется система вида:

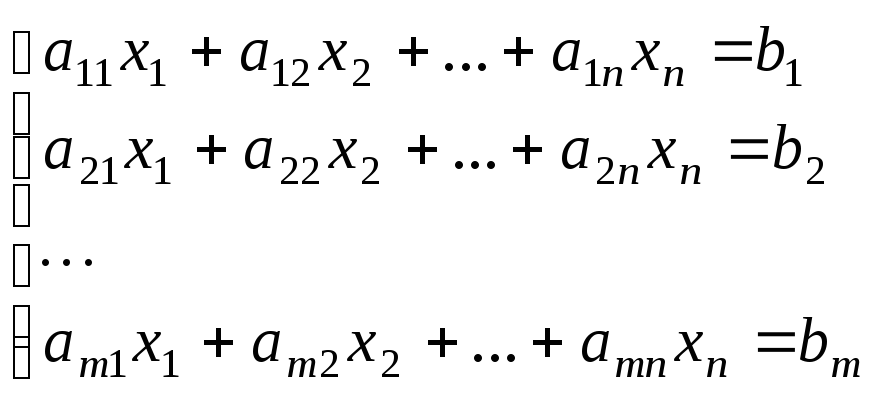(25)

где a_ij,b_i– числа;

a_ij–коэффициенты системы линейных уравнений;

b_i– свободные члены.

Сокращенно систему (25) можно представить в виде:

,. (26)

Система уравнений (25) может быть представлена в матричной форме, т. е. в виде матричного уравнения:

, (27)

где 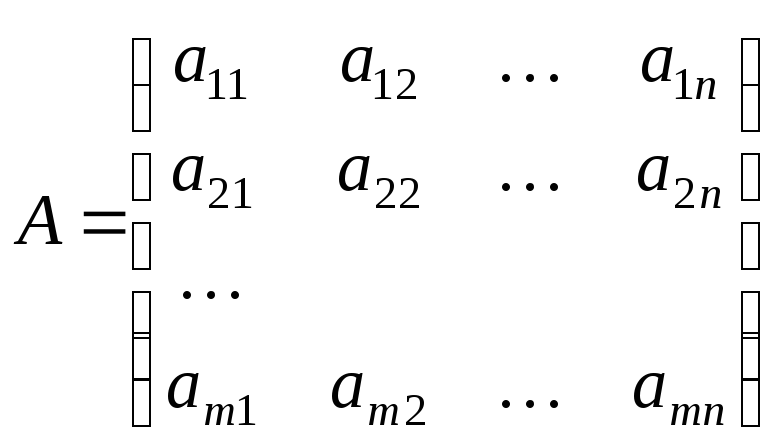– матрица коэффициентов системы линейных уравнений,

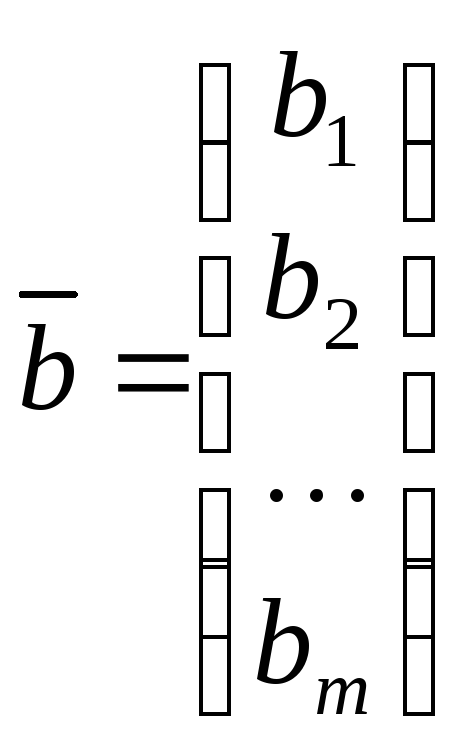,– вектор неизвестных и вектор свободных членов соответственно.

Решить систему уравнений (25) – значит найти такие значения х₁, x₂, , х_n, которые превращали бы все уравнения системы (25) в тождества.

Например, пусть имеется система уравнений

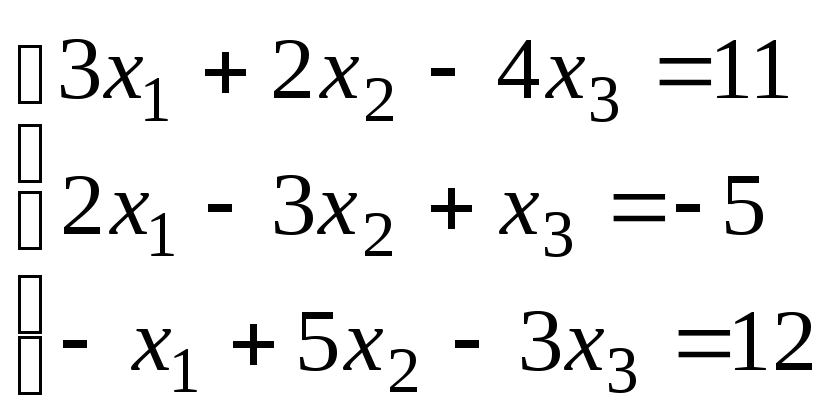. (28)

Система (28) может быть представлена в матричной форме:

или при вводе обозначений

,,

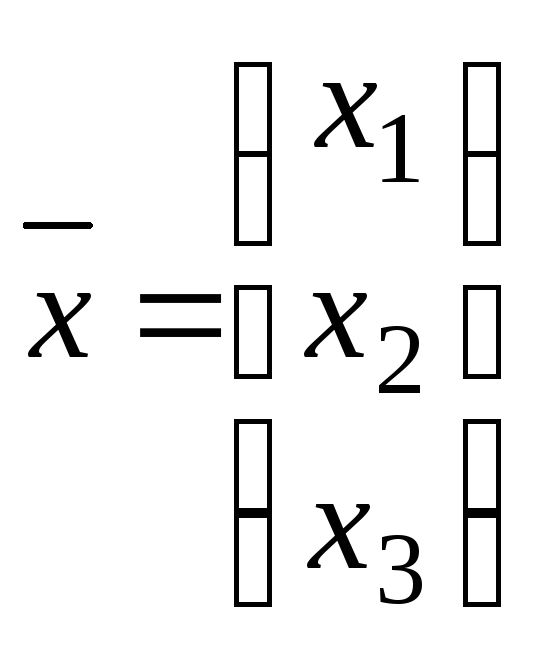в виде (27): .

Решением системы будет: x₁=1, x₂=2, x₃= – 1.

Решение системы линейных уравнений требует специальных математических методов.

Рассмотрим систему линейных уравнений 2-го порядка.

(29)

Возможны следующие варианты решения системы (29):

1. Решение единственно (рис. 35), определитель системы 0:

Например,

.

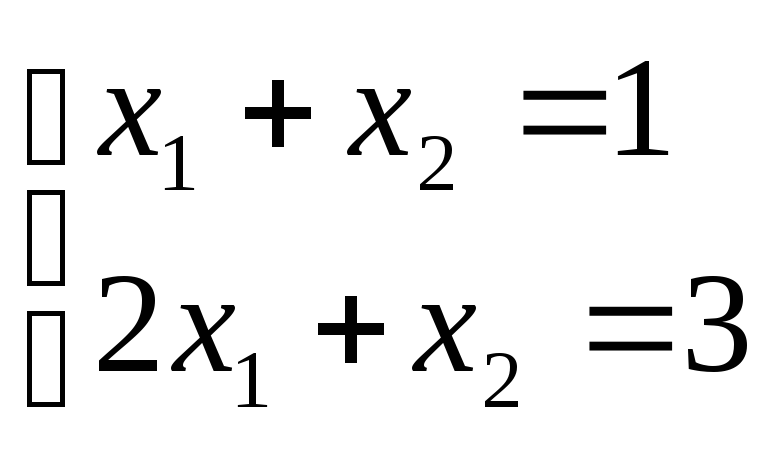Рис. 35. Решение системы единственно

2. Решений нет (рис. 36), определитель системы  = 0. Система называется вырожденной.

Например,

.

.

Рис. 36. Решений системы нет

3. Решений бесчисленное множество (рис. 37), определитель системы  = 0. Система называется вырожденной:

Например,

.

.

Рис. 37. Решений бесчисленное множество

4.Плохо обусловленные системы (рис. 38), определитель системы  близок к 0. Возможность получения единственного решения зависит от точности вычислений, производимых при решении, при разработке алгоритмов решения стараются предусмотреть методы борьбы с плохой обусловленностью (например, повышение точности счета).

Рис. 38. Плохо обусловленные системы

Для решения систем линейных уравнений существуют две группы методов: точные и приближенные методы.

Точные методы– это такие методы, в которых в принципе можно получить конечный результат, предполагая, что все коэффициенты и все промежуточные вычисления с ними выполняются точно.

Приближенные методы– методы, которые, даже в предположении точности всех промежуточных вычислений, дают только приближенное решение. Причем это решение можно получить с любой заранее заданной степенью точности.

Рассмотрим числовую ось (рис. 39).

Рис. 39. Числовая ось

Получить решение с заданной степенью точности – значит найти такое значениех, которое попало бы вокрестность относительноx*, гдеx*– точное решение.

Точные и приближенные методы имеют свои достоинства и недостатки.

Достоинством приближенных методов является их простота, возможность самоисправления ошибок, допущенных при обработке результатов.

Рассмотрим следующие точные методы решения систем линейных алгебраических уравнений:

• метод Крамера;

• метод Гаусса;

• метод обращения матриц

и приближенные итерационные методы:

• метод простых итераций;

• метод Зейделя.

6.2. Точные методы решения систем линейных уравнений

6.2.1. Метод Крамера

Пусть имеется система уравнений 3-го порядка

, (30)

где

,,

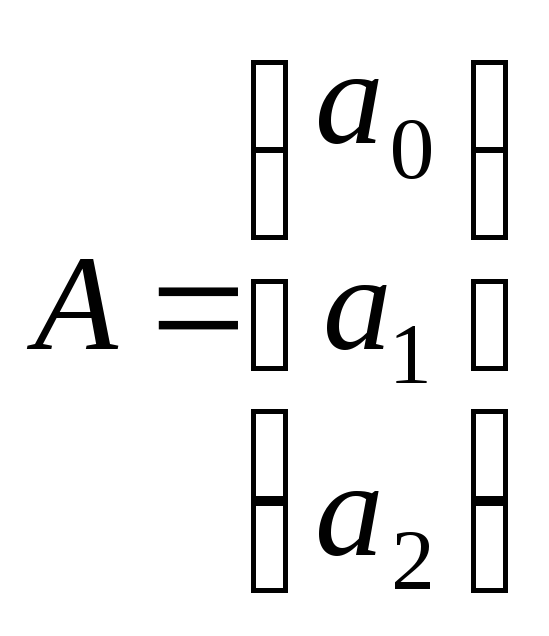
или в матричном виде

СA=Y,

где C– матрица коэффициентов системы;A– вектор неизвестных;Y– вектор правых частей.

Согласно теореме Крамера, решение (30) может быть найдено из формулы:

, (31)

где C_i– матрицаC, у которойi-й столбец заменен вектором свободных членов – векторомY.

Т. е.

Найдем определители матриц С, С₀,С₁, С₂.

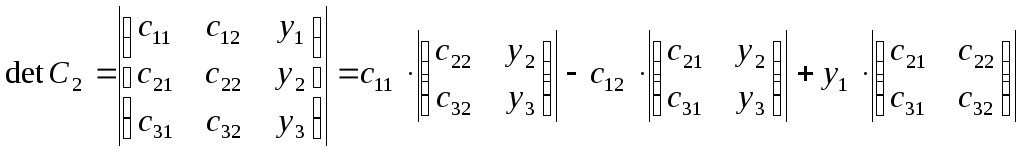
В Mathcadсуществует встроенная функция для расчета определителя матрицы. Она вызывается нажатием кнопкиDeterminant(Вычисление определителя) на панелиMatrix(Матрицы) (рис. 40).

Рис. 40. Вызов вычисления определителя матрицы

Зная определители, найдем a₀, a₁, a₂.

,,.

Пример решения системы линейных алгебраических уравнений методом Крамера.

Запрограммируем в Mathcadпроцесс решения системы методом Крамера. Имеем систему:

(32)

Запишем систему (32) в матричном виде:

или при вводе обозначений

,,

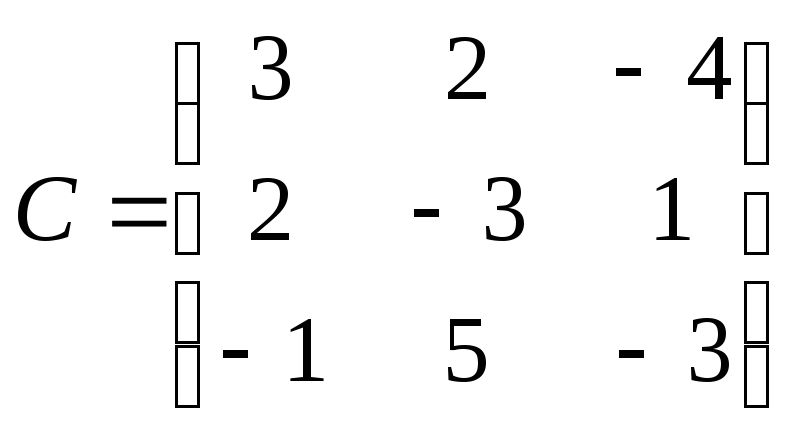Сa=Y.

1. Зададим системную переменную

2. Зададим исходные значения матрицы системы и вектора свободных членов

3. Сформируем ещё три матрицы

4. Рассчитаем определитель матрицы С

5. Проверим правильность расчета с помощью встроенной функции Mathcad

6. Рассчитаем остальные определители и проводим проверку правильности расчета.

7. Найдем решение системы и высвечиваем результат

8. Осуществим проверку решения системы

Результаты совпали, следовательно, решение верно.