6. Момент инерции

Момент инерции - величина, характеризующая  распределения масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. 

Момент инерции тела относительно оси вращения  зависит от массы тела и от распределения этой массы. Чем больше масса тела и  чем дальше она отстоит от воображаемой оси, тем большим моментом инерции обладает тело. Момент инерции элементарной (точечной) массы m_i, отстоящей от оси на расстоянии r_i, равен:

 

.

 

Момент инерции всего тела относительно оси равен:

 

 

или, для непрерывно распределенной массы:

 

.

 

Момент инерции всего тела сложной конфигурации обычно определяют экспериментально.

Момент инерции некоторых однородных твердых приведены в таблице 1.

 

		Таблица 1
Момент инерции некоторых симметричных однородных тел
Твердое тело	Ось вращения	Момент инерции I, кг м2
Тонкий стержень длины l	Перпендикулярна стержню, проходит через центр масс	ml2/12
Тонкий стержень длины l	Перпендикулярна стержню, проходит через край	ml2/3
Сплошной цилиндр радиуса R	Совпадает с осью цилиндра	mR2/2
Полый цилиндр радиуса R	Совпадает с осью цилиндра	mR2
Шар радиуса R	Проходит через центр шара	2mR2/5
Полый шар радиуса R	Проходит через центр шара	2mR2/3
Тонкий диск радиуса R	Совпадает с диаметром диска	mR2/4
Тонкая прямоугольная пластина со сторонами а и b	Проходит через центр пластины перпендикулярно пластине	m (a2+b2)/12

 

Вычисление моментов инерции во многих случаях можно упростить, используя соображения симметрии и теорему Штейнера. Согласно теореме Штейнера момент инерции тела относительно какой-либо оси I_A равен моменту инерции тела равен инерции тела относительно параллельной оси, проходящей через центр масс I_C, сложенному с величиной ma², где a - расстояние между осями: 

 

I_A = I_C + ma².

 

Понятием о моменте инерции широко пользуются при решении многих задач механики и техники. 

7. ---------------------------

8. Гидромеханика. Уравнение Навье - Стокса

Уравнения Навье — Стокса описывают движение вязкой ньютоновской жидкости и являются основой гидродинамики. Численные решения уравнений Навье — Стокса используются во многих практических приложениях и научных работах. Однако в аналитическом виде решения этих уравнений найдены лишь в некоторых частных случаях, поэтому нет полного понимания свойств уравнений Навье — Стокса. В частности, решения уравнений Навье — Стокса часто включают в себя турбулентность, которая остаётся одной из важнейших нерешённых проблем в физике, несмотря на её огромную важность для науки и техники.

[Править]Уравнения Навье — Стокса

Основная статья: Уравнения Навье — Стокса

В математике это система нелинейных дифференциальных уравнений в частных производных для абстрактных векторных полей любой размерности. В физике это система уравнений, которая в рамках механики сплошных сред описывает движение жидкостей или неразреженных газов.

Пусть  — трёхмерный вектор скорости жидкости,  — давление. Тогда уравнения Навье — Стокса записываются так:

где  — это кинематическая вязкость,  — плотность,  — внешняя сила,  — оператор набла и  — оператор Лапласа (лапласиан), который также обозначается, как . Отметим, что это векторное уравнение, то есть оно содержит три скалярных уравнения. Если обозначить компоненты векторов скорости и внешней силы, как

то для каждого значения получается соответствующее скалярное уравнение Навье — Стокса:

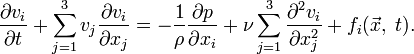
Неизвестными величинами являются скорость и давление . Поскольку в трёхмерном случае получается три уравнения и четыре неизвестных (три компоненты скорости и давление), то необходимо ещё одно уравнение. Дополнительным уравнением является закон сохранения массы

Если среду считать несжимаемой, то это уравнение преобразуется в условие несжимаемости жидкости: