Полуклассическая теория Бора[править]

Основана на двух постулатах Бора:

• Атом может находиться только в особенных стационарных, или квантовых, состояниях, каждому из которых отвечает определенная энергия. В стационарном состоянии атом не излучает электромагнитных волн.

• Излучение и поглощение энергии атомом происходит при скачкообразном переходе из одного стационарного состояния в другое, при этом имеют место два соотношения:

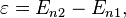1.  где  — излучённая (поглощённая) энергия, 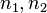 — номера квантовых состояний. В спектроскопи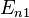и и 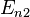называются термами.

2. Правило квантования момента импульса: 

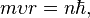
Далее исходя из соображений классической физики о круговом движении электрона вокруг неподвижного ядра по стационарной орбите под действием кулоновской силы притяжения, Бором были получены выражения для радиусов стационарных орбит и энергии электрона на этих орбитах:

 м — боровский радиус.

  — энергетическая постоянная Ридберга (численно равна 13,6 эВ).

Формула Зоммерфельда — Дирака[править]

Движение электрона вокруг атомного ядра в рамках классической механики можно рассматривать как «линейный осциллятор», который характеризуется «адиабатичным инвариантом», представляющим собой площадь эллипса (в обобщенных координатах):

где —  — обобщенный импульс и координаты электрона,  — энергия,  — частота. А квантовый постулат утверждает, что площадь замкнутой кривой в фазовой  — плоскости за один период движения, равна целому числу умноженному на постоянную Планка (Дебай, 1913 г.). С точки зрения рассмотрения постоянной тонкой структуры наиболее интересным является движение релятивистского электрона в поле ядра атома, когда его масса зависит от скорости движения. В этом случае мы имеем два квантовых условия:

, ,

где определяет главную полуось эллиптической орбиты электрона (), а  — его фокальный параметр :

, .

В этом случае Зоммерфельд получил выражение для энергии в виде

.

где  — постоянная Ридберга, а  — порядковый номер атома (для водорода ).

Дополнительный член отражает более тонкие детали расщепления спектральных термов водородоподобных атомов, а их число определяется квантовым числом . Таким образом сами спектральные линии представляют собой системы более тонких линий, которые соответствуют переходам между уровнями высшего состояния () и низшего состояния (). Это и есть т. н. тонкая структура спектральных линий. Зоммерфельд разработал теорию тонкой структуры для водородоподобных атомов (H, , ), а Фаулер с Пашеном на примере спектра однократно ионизированного гелия установили полное соответствие теории с экспериментом.

Зоммерфельд (1916 г.) еще задолго до возникновения квантовой механики Шредингера получил феноменологичную формулу для водородных термов в виде:

,

где  — постоянная тонкой структуры,  — порядковый номер атома,  — энергия покоя,  — радиальное квантовое число, а  — азимутальное квантовое число. Позднее эту формулу получил Дирак используя релятивистское уравнения Шредингера. Поэтому сейчас эта формула и носит имя Зоммерфельда — Дирака.

Появление тонкой структуры термов связана с прецессией электронов вокруг ядра атома. Поэтому появление тонкой структуры можно обнаружить по резонансному эффекту в области ультракоротких электромагнитных волн. В случае (атом водорода) величина расщепления близка к

Поскольку длина электромагнитной волны равна

Поэтому для это будет почти 1 см.