
- •Власов м. П.
- •2. Сфера применения графических средств для описания экономико-математических моделей
- •3. График Ганта
- •4. Элементы теории графов
- •5. Сетевая модель
- •6.Деревья и сфера их применения
- •Основные понятия, используемые для описания дерева свойств
- •7. Паутинообразная модель
- •8.Задачи изменения состояний системы
5. Сетевая модель
Сетевая модель представляет ориентированный антисимметричный конечный граф, отображающий технологию осуществления сложного проекта. Сетевые модели используются в экономическом анализе, планировании и управлении, и позволяют:
определить ближайший возможный срок завершения проекта;
выяснить выполнение каких работ определяет завершение проекта;
оценить резервы времени для каждой работы сетевого графика.
Сетевые модели это эффективный инструмент разработки календарных графиков, позволяющий осуществить:
оптимальное распределение имеющихся ресурсов (либо сводящее к минимуму потребности в них при своевременном осуществлении проекта, либо приближающее дату этого настолько, насколько допускают их наличные объемы);
контроль за выполнением работ в соответствии с заданной технологией;
поиск наилучших путей компенсации возникающих отклонений.
Первые системы, использующие сетевые графики, получили названия CPM (метод критического пути) и PERT (метод оценки и обзора программы). В России работы по сетевому планированию начались в 60-х годах. Система сетевого планирования впервые применена в США в 1959 году как основа метода обзора и оценки программ (PERT – Program Evaluation and Review Technique), связанных с ракетным проектом «Поларис». По этому проекту проектировались одновременно и ракетная система, собственно «Поларис», и платформа, ее носитель - атомная подводная лодка «Дж. Вашингтон». В дальнейшем American Management Association распространила этот метод на все функции управления взаимодействующими фирмами. Метод имеет несколько разновидностей:
PERT-Time (оптимизация по времени);
PERT-Cost и PERT-Reliability (оптимизация по затратам и надежности);
«Линия баланса» (оценка фактического состояния реализации проекта по времени, стоимости, проценту готовности на основе принципа отклонений от плана).
В России сетевые модели используются с начала 1960-х годов. Благодаря универсальности содержательной интерпретации они используются во многих сферах деятельности – от всех видов строительства, судостроительной, авиационно-космической, добывающей промышленности до киноиндустрии, научных исследований, реформирования экономики и предприятий.
В начале 70-х были разработаны оригинальные сетевые модели более гибкие и мощные, чем модели СРМ или PERT. Эти модели, так называемые обобщенные сетевые модели (ОСМ), особенно полезны для описания сложных проектов с различными взаимосвязями между работами и временными ограничениями разного типа. Тогда же был разработан спектр стохастических и альтернативных моделей, учитывающих вероятностную природу различных элементов проекта.
Сетевое планирование и управление (СПУ) основано на моделировании процесса с помощью сетевого графика и представляет собой совокупность расчетных методов, организационных и контрольных мероприятий по планированию и управлению комплексом работ.
Система СПУ позволяет:
формировать календарный план реализации некоторого комплекса работ;
выявлять и мобилизовывать резервы времени, трудовые, материальные и денежные ресурсы;
осуществлять управление комплексом работ по принципу «ведущего звена» с прогнозированием и предупреждением возможных срывов в ходе работ;
повышать эффективность управления в целом при четком распределении ответственности между руководителями разных уровней и исполнителями работ.
Диапазон применения СПУ весьма широк: от задач, касающихся деятельности отдельных лиц, до проектов, в которых участвуют сотни организаций и десятки тысяч людей (например, разработка и создание крупного территориально промышленного комплекса).
Под комплексом понимается всякая задача, для выполнения которой необходимо осуществить достаточно большое количество разнообразных действий. Это может быть и строительство здания, корабля, самолета, или создание любого другого сложного объекта, и разработка проекта этого сооружения, и собственно процесс построения планов реализации проекта.
Основными понятиями сетевой модели являются: событие, работа и путь. На рис. 5.1. представлена сетевая модель, состоящая из восьми событий и тринадцати работ, продолжительность выполнения которых указана над (под) работами.
Работа характеризует материальное действие, требующее использования ресурсов, или логическое, требующее лишь взаимосвязи событий.
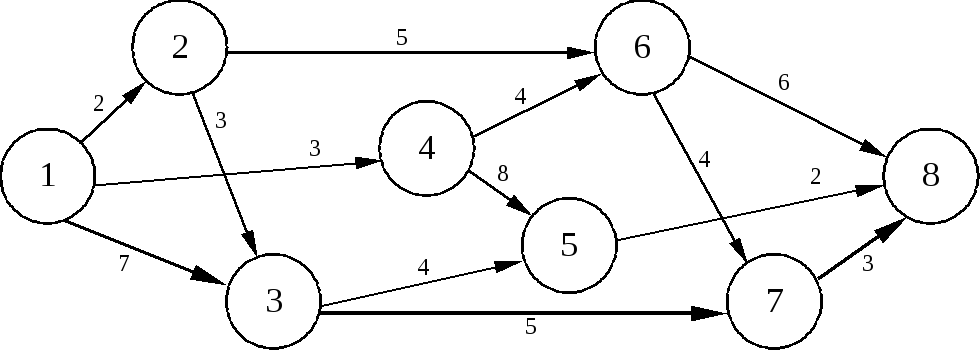
Рис. 5.1. Сетевая модель
Событиями называются результаты выполнения одной или нескольких работ. Они не имеют протяженности во времени и свершаются в тот момент, когда оканчивается последняя из работ, входящая в него. Событие фиксирует факт получения результата, оно не имеет продолжительности во времени.
Событие имеет двойственный характер: для всех непосредственно предшествующих ему работ событие является конечным, а для всех непосредственно следующих за ним – начальным. В сети всегда существуют, по крайней мере, одно исходное и одно завершающее события.
На графе события изображаются кружками (вершинами), а работы – стрелками (ориентированными дугами), показывающими связь между работами.
Путь – это последовательность работ, соединяющих начальную и конечную точки вершины.
Визуально сетевая
модель, называемой иногда стрелочной
диаграммой или сетью, это – множество
точек-вершин (![]() )
вместе с соединяющими их ориентированными
дугами. Каждая из них как направленный
отрезок имеет начало и конец, причем
модель содержит лишь одну пару симметричных
дуг
)
вместе с соединяющими их ориентированными
дугами. Каждая из них как направленный
отрезок имеет начало и конец, причем
модель содержит лишь одну пару симметричных
дуг![]() и
и![]() .
Всякой дуге, рассматриваемой в качестве
какой-то работе из числа нужных для
осуществления проекта, приписываются
определенные количественные характеристики.
Это – объемы выделяемых для нее ресурсов
и, соответственно, ее ожидаемая
продолжительность (длина дуги). Любая
вершина интерпретируется как событие
завершения работ, представленных дугами,
которые входят в нее, и одновременно
начала работ, отображаемых дугами,
исходящими оттуда. Таким образом,
фиксируется, что ни к одной из работ
нельзя приступить прежде, чем будут
выполнены все предшествующие ей согласно
технологии реализации проекта. Факт
начала этого процесса – вершина без
входящих, а окончания – без исходящих
дуг. Остальные вершины должны иметь и
те и другие.
.
Всякой дуге, рассматриваемой в качестве
какой-то работе из числа нужных для
осуществления проекта, приписываются
определенные количественные характеристики.
Это – объемы выделяемых для нее ресурсов
и, соответственно, ее ожидаемая
продолжительность (длина дуги). Любая
вершина интерпретируется как событие
завершения работ, представленных дугами,
которые входят в нее, и одновременно
начала работ, отображаемых дугами,
исходящими оттуда. Таким образом,
фиксируется, что ни к одной из работ
нельзя приступить прежде, чем будут
выполнены все предшествующие ей согласно
технологии реализации проекта. Факт
начала этого процесса – вершина без
входящих, а окончания – без исходящих
дуг. Остальные вершины должны иметь и
те и другие.
Последовательность дуг, в которой конец каждой предшествующей совпадает с началом последующей, трактуется как путь от отправной вершины к завершающей, а сумма длин таких дуг – как его продолжительность. Обычно начало и конец реализации проекта связаны множеством путей, длины которых различаются. Наибольшая определяет длительность всего этого процесса, минимально возможную при зафиксированных характеристиках дуг графа. Соответствующий путь называется критическим. В каждый момент времени с помощью критического пути можно контролировать процесс, определяя состояние именно тех работ, которые принадлежат критическому пути.
Построению сетевой
модели предшествует систематизация
технологической и экономической
информации о проекте. Каждой требуемой
работе присваивается наименование по
номерам ее начального и конечного
событий, например,
![]() ,
и указываются:
,
и указываются:
работы, начинать которые следует по ее завершении, скажем,
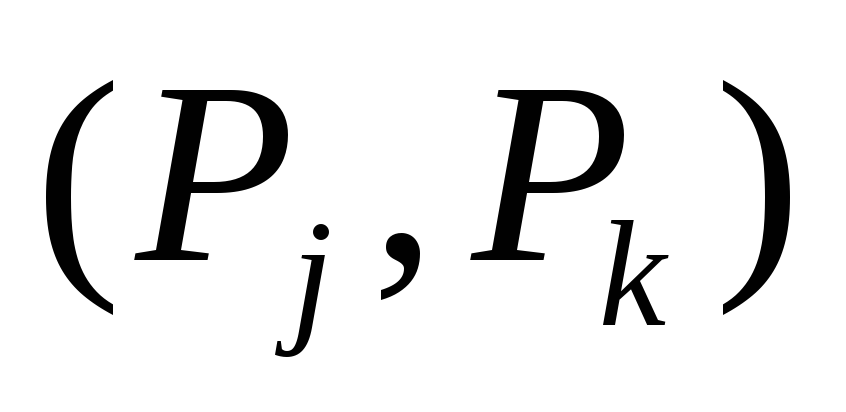 ,
,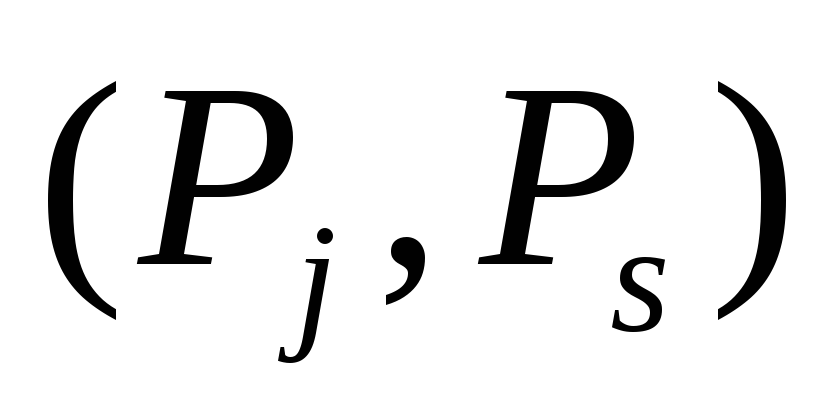 ;
;объем дефицитных ресурсов, выделяемых для выполнения работы
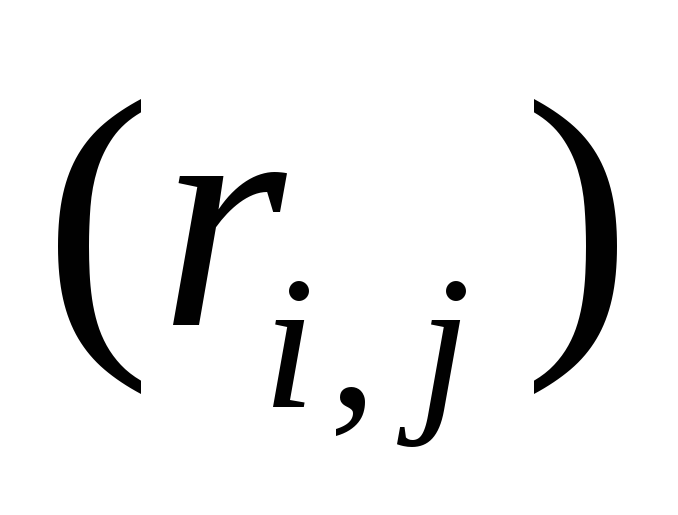 ;
;сроки выполнения работы (на взгляд экспертов – пессимистический и оптимистический, соответственно, при прочих неблагоприятных обстоятельствах и в противоположной ситуации (
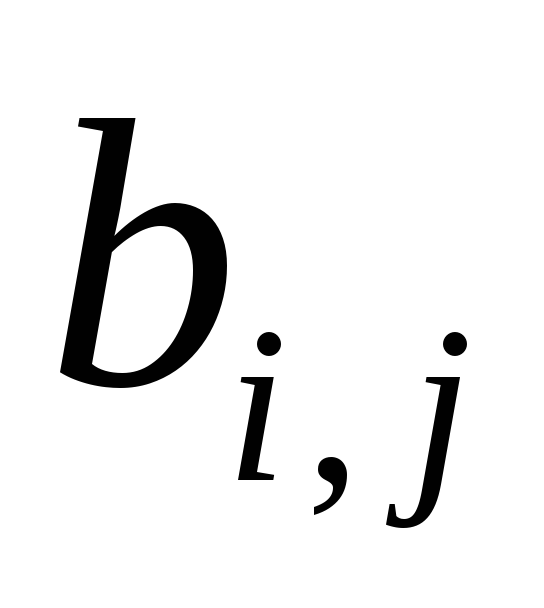 и
и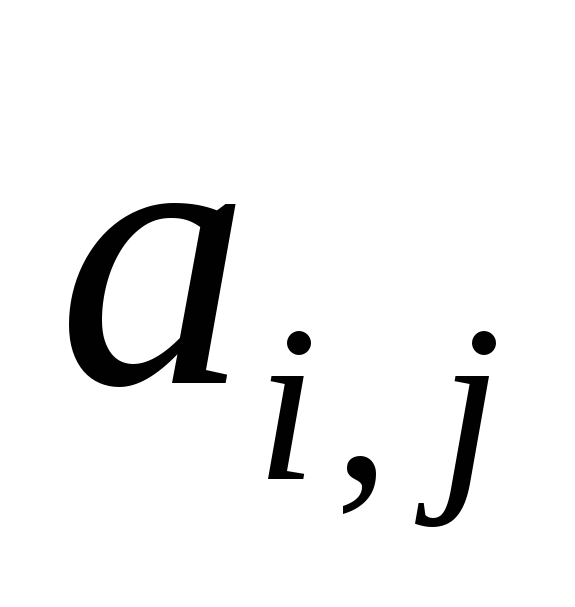 ),
по опыту – среднестатистический
(
),
по опыту – среднестатистический
(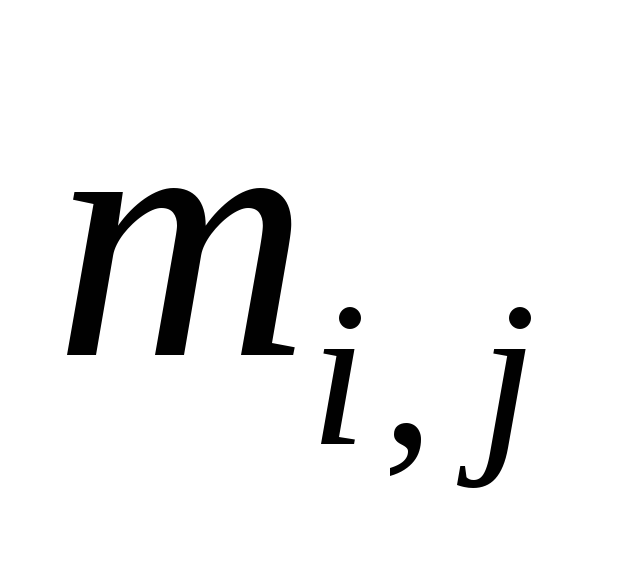 )).
)).
Исходя из них
рассчитывается ожидаемая длительность
работ -
![]() ,
причем если заданы три оценки
продолжительности работы, то расчет
производится по формуле:
,
причем если заданы три оценки
продолжительности работы, то расчет
производится по формуле:
![]() ,
,
а если только две, то используется другая формула:
![]() .
.
Такая систематизация считается выполненной правильно, если сеть, сформированная на базе ее итогов, не содержит ни одного замкнутого цикла (последовательность дуг, оканчивающаяся вершиной, послужившей ее началом). Иногда оказывается, что два события связаны несколькими параллельными работами, одна из них отображается непосредственно между соответствующими вершинами, а каждая другая – последовательностью из двух дуг (обозначающих действительную работу и фиктивную с нулевой продолжительностью или ожидание завершения остальных). Операция, выполнение каких-то частей которой достаточно, чтобы приступить к другим работам, представляется в сети несколькими последовательными дугами - образами этих частей как простых работ. Если вершина фиксирует завершение нескольких работ и начало ряда иных, для отдельных из них возможное независимо от окончания каких-то предшествующих, то в граф вводится нужное число дополнительных вершин, связываемых с ней фиктивными работами и означающих, с одной стороны, начало каких реально, с другой же – завершение только сдерживающих их.
Проект бывает многоцелевым, с несколькими конечными событиями. Тогда на сети с какой-то из соответствующих вершин все остальные, отображающие такие события, связываются фиктивными работами. При необходимости подробную сеть можно укрупнить, представив тот или иной ее участок, связанный и с предшествующей, и с последующей частью графа единственным образом, как одну работу, продолжительность которой оценивается по длине критического пути этого участка.
Анализ сетевой
модели требует упорядочения вершин
сети, чтобы для любой дуги
![]() выполнялось условие
выполнялось условие![]() .
Самый простой способ добиться этого
– присвоить каждой вершине числовой
ранг, равный максимальному количеству
дуг, связывающих ее с началом графа, а
затем вершинам одного и того же ранга
(начиная с наименьшего, и т.д. в порядке
возрастания) – произвольные номера.
.
Самый простой способ добиться этого
– присвоить каждой вершине числовой
ранг, равный максимальному количеству
дуг, связывающих ее с началом графа, а
затем вершинам одного и того же ранга
(начиная с наименьшего, и т.д. в порядке
возрастания) – произвольные номера.
Такой анализ
предполагает вычисление, прежде всего,
![]() (наиболее раннего возможного срока
наступления события
(наиболее раннего возможного срока
наступления события![]()
![]() ,
а когда
,
а когда![]() ,
длины критического пути или времени
выполнения проекта) и
,
длины критического пути или времени
выполнения проекта) и![]() (при
(при![]() - наиболее позднего допустимого
момента завершения любой из работ, не
затягивающего реализацию всего
проекта):
- наиболее позднего допустимого
момента завершения любой из работ, не
затягивающего реализацию всего
проекта):
![]() ;
;
![]() ;
;
![]() .
.
На основе этих показателей рассчитываются:
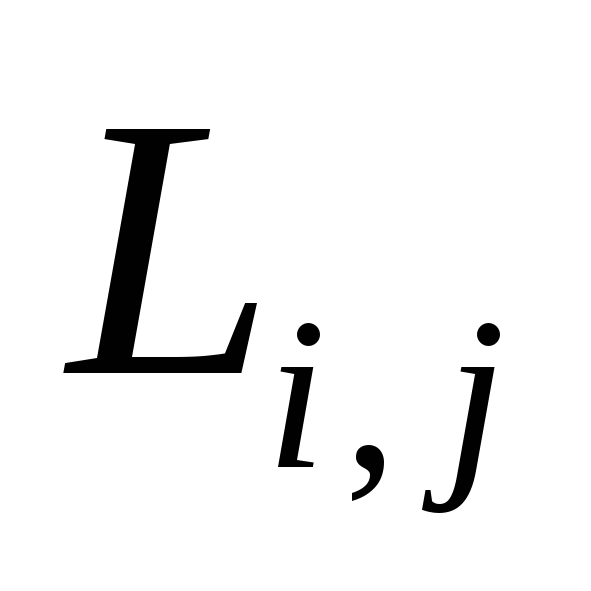 - свободный резерв
времени каждой работы или максимальное
увеличение ее продолжительности
(запаздывание с началом), не мешающее
приступить к остальным в наиболее
раннее возможное для каждой из них
время;
- свободный резерв
времени каждой работы или максимальное
увеличение ее продолжительности
(запаздывание с началом), не мешающее
приступить к остальным в наиболее
раннее возможное для каждой из них
время;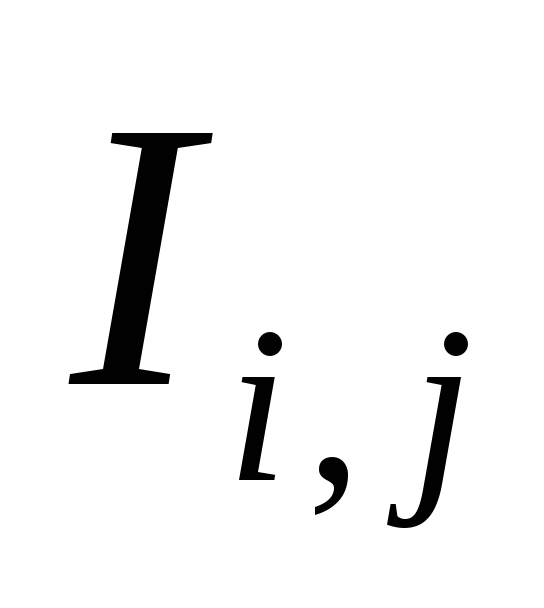 - независимый
резерв времени любой работы или
максимальное допустимое увеличение
ее продолжительности (запаздывание
с началом) при условии, что все остальные
работы, завершаемые событием
- независимый
резерв времени любой работы или
максимальное допустимое увеличение
ее продолжительности (запаздывание
с началом) при условии, что все остальные
работы, завершаемые событием
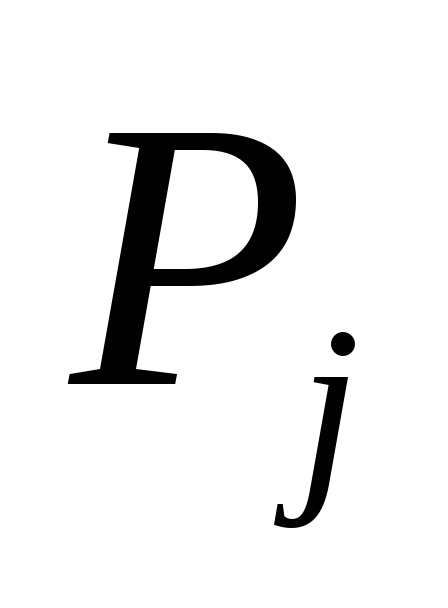 ,
оканчиваются в наиболее позднее
допустимое для каждой время, а ко всем,
факт начала которых фиксируется
событием
,
оканчиваются в наиболее позднее
допустимое для каждой время, а ко всем,
факт начала которых фиксируется
событием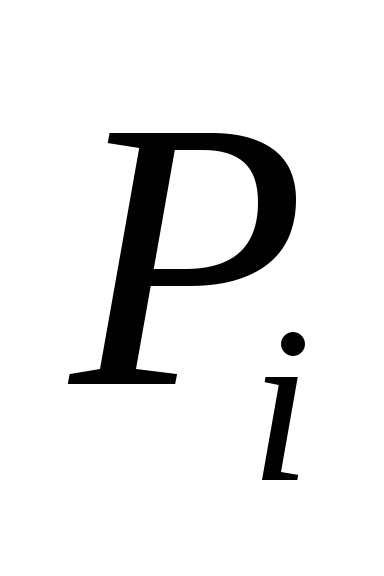 ,
приступают в наиболее раннее возможное
время;
,
приступают в наиболее раннее возможное
время;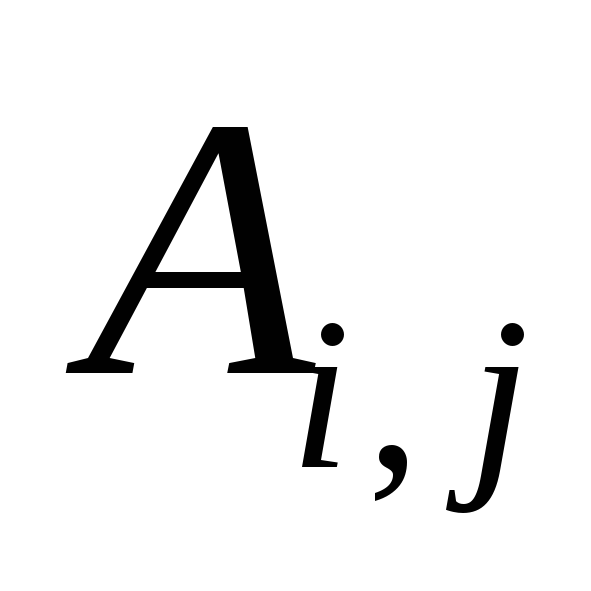 - полный резерв
времени каждой работы или максимальное
увеличение ее продолжительности,
которое не скажется на сроке выполнения
всего проекта;
- полный резерв
времени каждой работы или максимальное
увеличение ее продолжительности,
которое не скажется на сроке выполнения
всего проекта;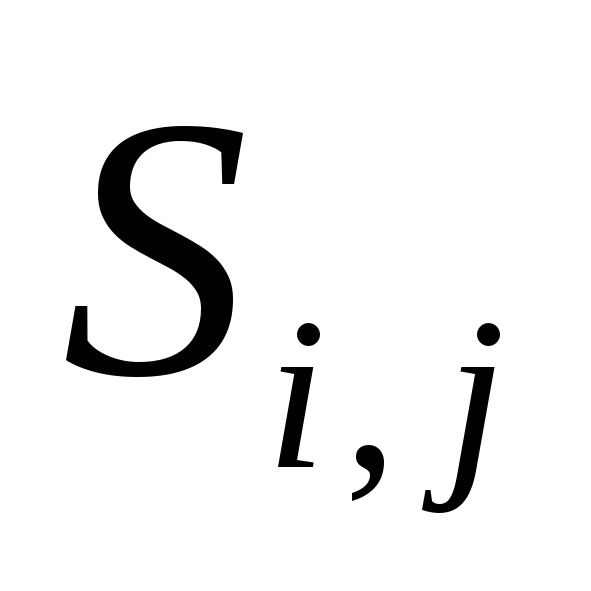 - коэффициенты,
характеризующие напряженность
выполнения отдельных работ как
отношение полного резерва времени
каждой к тому периоду, в течение которого
он может быть реализован (чем меньше
это отношение, тем выше такой коэффициент
и напряженность выполнения работы).
- коэффициенты,
характеризующие напряженность
выполнения отдельных работ как
отношение полного резерва времени
каждой к тому периоду, в течение которого
он может быть реализован (чем меньше
это отношение, тем выше такой коэффициент
и напряженность выполнения работы).
При этом
![]() ;
;
![]() ;
;
![]() ;
;
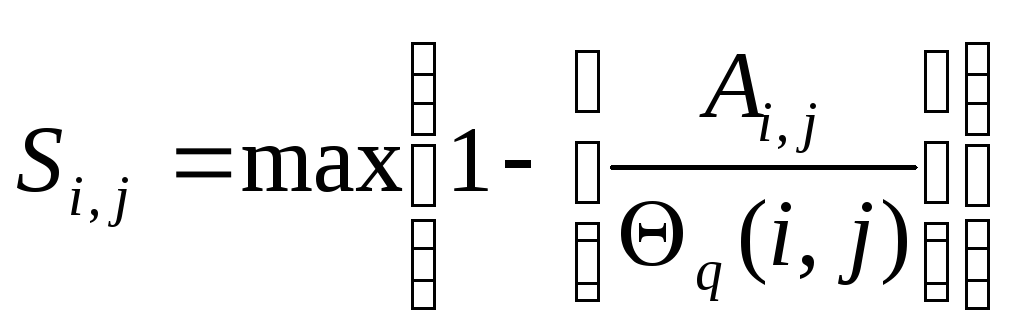 ,
,
где
![]() - длина того отрезка
- длина того отрезка![]() критического пути, который заключен
между событиями, ближайшими справа и
слева к работе
критического пути, который заключен
между событиями, ближайшими справа и
слева к работе![]() и расположенными на пути максимальной
длины, проходящем через нее (в сети может
быть несколько критических путей и
потому – таких отрезков). Более достоверные
оценки этих величин можно получить,
применив к результатам их расчета метод
статистических испытаний. Для этого
необходимо по другому задавать исходную
информацию и несколько изменить процедуры
ее последующей обработки.
и расположенными на пути максимальной
длины, проходящем через нее (в сети может
быть несколько критических путей и
потому – таких отрезков). Более достоверные
оценки этих величин можно получить,
применив к результатам их расчета метод
статистических испытаний. Для этого
необходимо по другому задавать исходную
информацию и несколько изменить процедуры
ее последующей обработки.
Оптимальная
организация выполнения проекта,
отображаемого сетевой моделью,
требует использовать понятие «фронт
работ», т.е. совокупность тех из них,
которые могут производится параллельно.
Отдельный, фронт
![]() (
(![]() при
при![]() )
характеризуется величинами
)
характеризуется величинами![]() (суммарный расход за единицу времени
некоторого ограниченного ресурса
широкого применения на все работы,
входящие в данный фронт) и
(суммарный расход за единицу времени
некоторого ограниченного ресурса
широкого применения на все работы,
входящие в данный фронт) и![]() (длительность его использования, равная
нулю), если
(длительность его использования, равная
нулю), если![]() превышает
превышает![]() - доступное количество дефицитного
ресурса. Здесь
- доступное количество дефицитного
ресурса. Здесь
![]()
Когда цель –
скорейшая реализация проекта, относительно
![]() решается задача
решается задача![]() при
при![]() .
.
Но затраты на выполнение каждой работы растут с убыванием ее продолжительности благодаря интенсификации, ибо для этого нужны дополнительные расходы. И если допустить, что эта продолжительность не ограничена сверху, при известном критическом пути сетевой модели и соответствующем ему сроке реализации проекта, требуется минимизировать ее общую стоимость, используя резервы времени по работам. Математически это – общая задача линейного программирования, решаемая симплекс-методом.
Пример расчета критического пути в приведенной на рис. 8.5.1. сетевой модели.
Наиболее эффективно при решении данной задачи является использование аппарата динамического программирования.
События сетевой модели целесообразно в этом случае упорядочить по этапам решения задачи, используя для этого следующий алгоритм.
1. Первому событию сетевой модели присвоить номер этапа «0».
2. Событиям, непосредственно следующим за нулевым этапом, присвоить номер этапа «1».
3. Событиям, непосредственно следующим за первым этапом, присвоить номер этапа «2» и т. д. до последнего события сетевой модели.
Р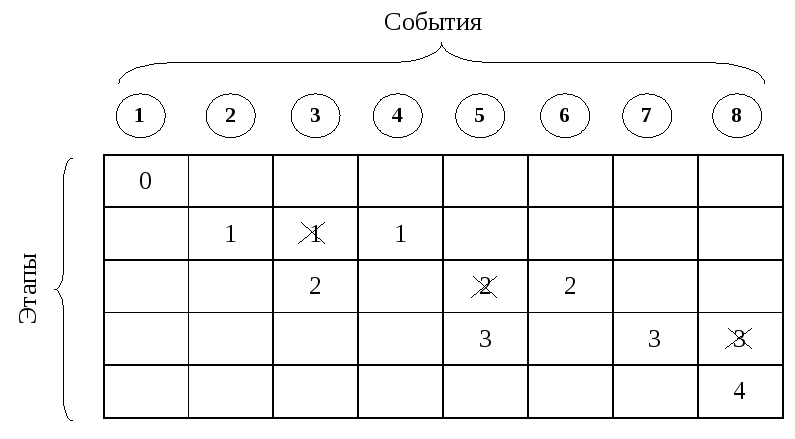 аботу
данного алгоритма можно наглядно
проиллюстрировать при помощи
нижеприведенной таблицы (рис.5.2.).
аботу
данного алгоритма можно наглядно
проиллюстрировать при помощи
нижеприведенной таблицы (рис.5.2.).
Рис. 5.2. Определение ранга события
Трансформированный таким образом (под метод динамического программирования) сетевой график будет иметь следующий вид (рис. 5.3.).
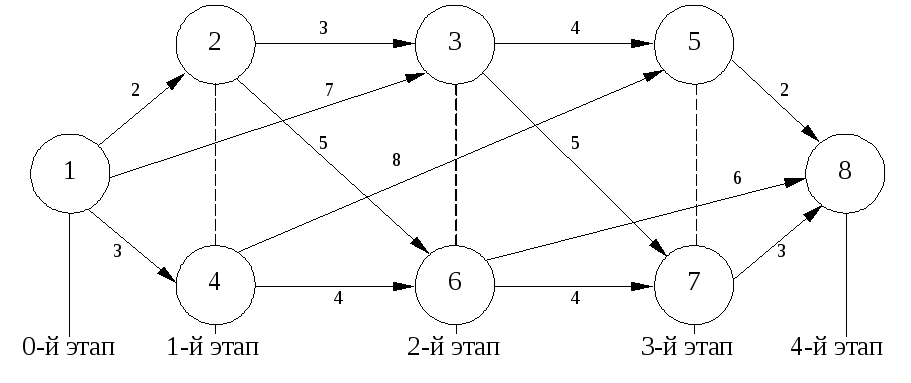
Рис. .5.3. Трансформированная по этапам расчета сетевая модель
Критический, т. е. самый длинный путь от начального события к конечному может быть рассчитан по следующей рекуррентной формуле:
![]() при
при
![]() ,
,
где
![]() – продолжительность работы между двумя
смежными событиями
– продолжительность работы между двумя
смежными событиями
![]() и
и![]() ;
;
![]() –самый
продолжительный путь от события
–самый
продолжительный путь от события
![]() до конечного события.
до конечного события.
Решение модели
Первая итерация (4-й этап):
![]() .
.
Вторая итерация (3-й этап):
F5 = max {x58 + F8} = 2.
F7 = max {x78 + F8} = 3.
Третья итерация (2-й этап):
F3
=
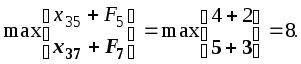
F6
=
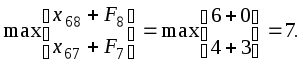
Четвертая итерация (1-й этап):
F2
=
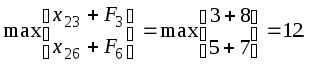
F4
=
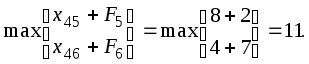
Пятая итерация (0-й этап):
F1
=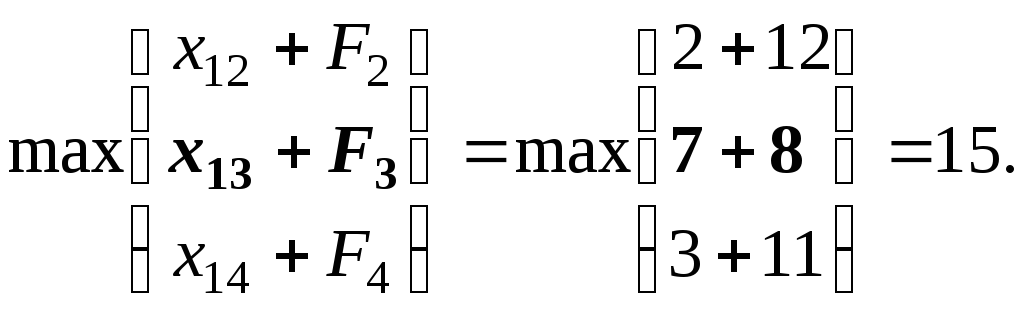
Таким образом, критическим в рассмотренной сетевой модели является путь через события 1, 3, 7, 8 с общей продолжительностью 15 единиц.
Читателям пособия предлагается самостоятельно найти критический путь на следующей сетевой модели (рис. 5.4.).
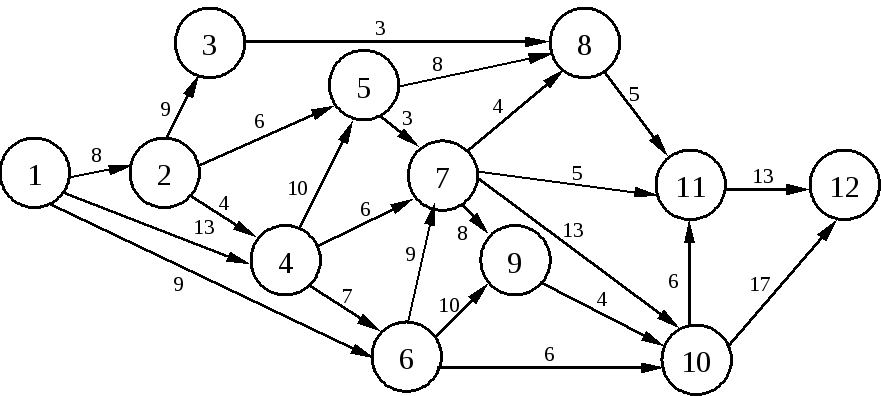
Рис. 5.4. Сетевая модель реализации условного проекта
В системах СПУ могут применяться следующие виды сетевых моделей:
По характеру отображения:
в терминах событий;
в терминах работ;
в терминах работ и событий.
Наиболее распространенным способом изображения сетей считаются сетевые модели в терминах работ и событий.
Термин работа используется в широком смысле:
работа – протяженный во времени процесс, требующий затрат ресурсов (например, сборка изделия, испытание прибора и т.п.).
ожидание – протяженный во времени процесс, не требующий затрат труда (например процесс старения металла, твердения бетона и т.п.).
зависимость или фиктивная работа – логическая связь между двумя или несколькими работами (событиями), не требующими затрат труда, материальных ресурсов и времени, указывающая, что возможность одной работы непосредственно зависит от результатов другой. Продолжительность фиктивной работы принимается равной нулю.
По степени охвата проекта различаются сети следующих уровней:
комплексные (сводные);
частные;
первичные.
По количеству независимых целей:
одноцелевые – сети с одним завершающим событием (работой).
многоцелевые – сети, имеющие одно исходное событие (работу) и несколько завершающих событий (работ).
По степени детализации:
укрупненные;
детализированные.
По степени неопределенности построения структура сети может быть:
детерминированной, если все работы проекта и их взаимосвязь точно определены.
стохастической, если все работы проекта включены в сеть с некоторой вероятностью.
смешанной, если наличие некоторых работ в сети определено с некоторой вероятностью, а остальные работы, входящие в сеть, имеют детерминированную структуру.
По степени неопределенности оценок:
с детерминированными оценками;
со случайными (стохастическими) оценками.
Первые используются в тех случаях, когда предполагаемая продолжительность работ может быть определена точно. Если же работа обладает большой неопределенностью и ее продолжительность не поддается точному определению, то используются вероятностные оценки.
