Возрастная таблица производства и потребления

	5-9	10-14	15-19	20-24	25-29	30-34
	0.64	0.82	0.99	1.19	1.38	1.29
	0	0.71	0.71	0.90	1.05	1.10
	35-39	40-44	45-49	50-54	55-59
	1.29	1.17	1.09	1.09	1.09
	1.11	1.12	1.09	1.07	1.08

В таблице использованы обозначения:

- возраст;

- потребление в возрасте ;

- производство в возрасте ;

- средневозрастной уровень потребления;

- средневозрастной уровень производства.

Фактическое потребление в каждом возрасте пропорционально покупательной способности:

,

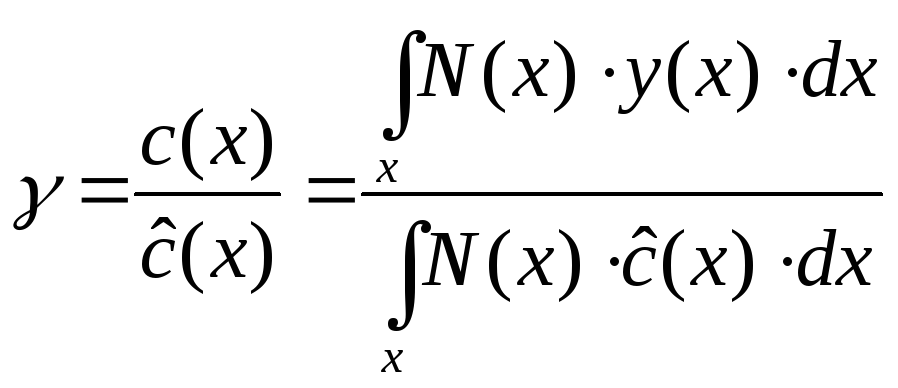где - коэффициент поддержки;

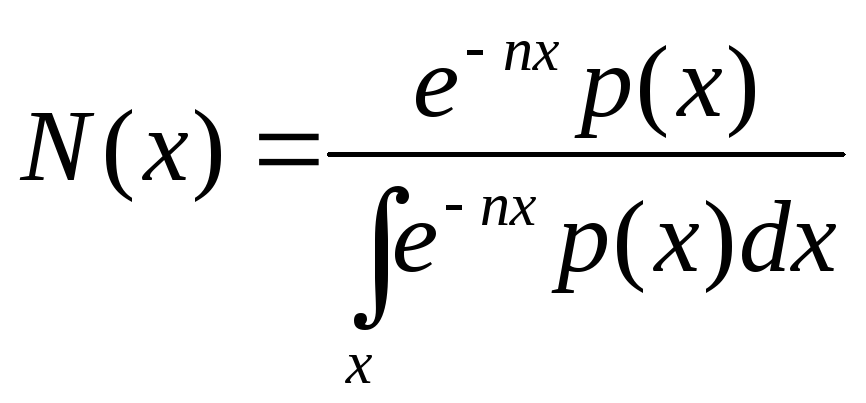- численность стабильного населения в возрасте ;

- темп роста численности стабильного населения;

- вероятность дожить до возраста .

Зависимость коэффициента поддержки от темпа роста численности населения выражается следующим образом:

,

где - средний возраст потребления;

- средний возраст производства.

Для оценки влияния демографического фактора на макроэкономические показатели в экономике народонаселения широко используются модели, основанные на регрессионных уравнениях. Параметры таких уравнений различны для экономически развитых и развивающихся стран, а также для различных периодов времени. Одной из таких моделей является модель валовых внутренних сбережений, предложенная Н. Леффом:

,

где - валовые внутренние сбережения;

- валовый внутренний продукт;

- численность населения;

- годовой темп роста среднедушевого валового внутреннего продукта;

- показатель демографической нагрузки детским населением (отношение численности населения в возрасте 0÷14 лет к численности населения в возрасте 15÷64 года);

- показатель демографической нагрузки пожилым населением (отношение численности населения в возрасте 65 лет и старше к численности населения в возрасте 15÷64 года);

- параметры уравнения.

Модель Р. Барро, рассматривающая социально-политические, экономические и демографические факторы, построена на основе данных за период с 1960года по 1985 год:

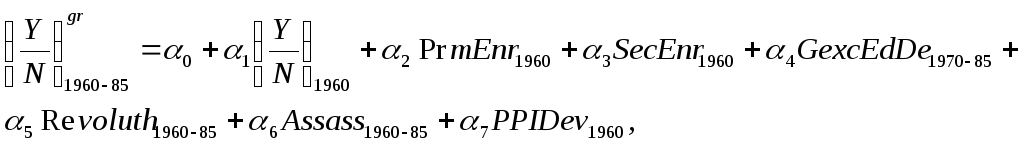
где - среднегодовые темпы роста валового внутреннего продукта (ВВП) на душу населения в 1960 – 1985 годах;

- ВВП на душу населения в 1960 году;

- полнота охвата начальным образованием населения соответствующего возраста в 1960 году;

- среднегодовая доля (в ВВП) государственных расходов, исключая расходы на образование и оборону, в 1970-85 годах;

- число революций (восстаний и т.п.) в 1960-85 годах;

- среднегодовое число умышленных убийств в расчете на 1 млн. человек населения в 1960-85 годах;

- абсолютная величина отклонения доли государственных инвестиций в основной капитал в 1960 году от средней величины за период с 1960 года по 1985 год;

- параметры уравнения.

Экономико-математические модели, предложенные А. Келли и Р. Шмидтом, относятся к наиболее надежным и статистически устойчивым. Их отличительной чертой является возможность расширения базовой модели за счет включения дополнительных факторов, значимость которых подтверждена на основе других моделей. При этом характер и сила влияния факторов, включенных в базовую модель, принципиально не меняется. Базовая и декомпозиционная (позволяющая разделить негативный и краткосрочный и позитивный долгосрочный эффект повышения рождаемости) модели Келли и Шмидта описываются уравнениями

,

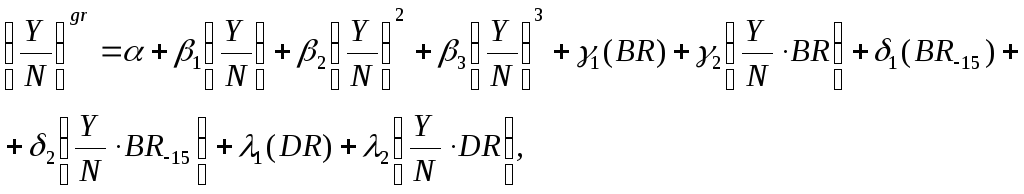
где - валовый внутренний продукт;

- численность населения;

- среднегодовой чистый (за вычетом младенческой смертности) общий коэффициент текущей рождаемости;

- среднегодовой чистый общий коэффициент прошлой (с15-летним лагом) рождаемости;

- общий коэффициент смертности;

- параметры регрессионного уравнения.

К экономике народонаселения относят и модели, основанные на концепции человеческого капитала и рассматривающие влияние качественных характеристик населения (образование, профессиональный опыт, здоровье) на экономику.