
- •Гласман К.Ф., Покопцева М.Н.
- •«Аудиовизуальная техника»
- •Введение
- •2. БАЗОВЫЕ ЛОГИЧЕСКИЕ СХЕМЫ
- •2.1. Логические элементы
- •2.1.1. Основные логические функции
- •2.1.2. Составление логических функций
- •2.1.3. Производные основных логических функций
- •2.1.4. Логические элементы как схемы временной селекции
- •2.1.5. Логические состязания
- •2.2 Триггеры
- •2.2.1 Бистабильная ячейка
- •2.2.2. Асинхронные и синхронные триггеры
- •2.2.3. Статический синхронный RS-триггер
- •2.2.4 Статический синхронный D-триггер
- •2.2.5 Триггеры типа M-S ("ведущий-ведомый")
- •2.2.6. Динамический D-триггер
- •3. КОМБИНАЦИОННЫЕ УСТРОЙСТВА
- •3.1. Преобразователи кодов
- •3.1.1. Шифраторы
- •3.1.2. Дешифраторы
- •3.1.4. Преобразователи двоичного кода в двоично-десятичный
- •3.1.5. Преобразователи двоично-десятичного кода в двоичный
- •3.1.6. Взаимное преобразование кода Грея и двоичного кода
- •3.1.7. Схемы контроля четности и нечетности
- •3.2. Мультиплексоры и демультиплексоры
- •3.2.1. Мультиплексоры
- •3.2.2. Мультиплексор как универсальная комбинационная схема
- •3.2.3. Демультиплексоры
- •3.3. Арифметические устройства
- •3.3.1. Компараторы
- •3.3.2. Одноразрядные сумматоры
- •3.3.3. Сумматоры с последовательным переносом
- •3.3.4. Сумматоры с параллельным переносом
- •3.3.5. Устройства для вычитания чисел

3 |
ВВЕДЕНИЕ |
|
|
|
|
ВВЕДЕНИЕ
Системы формирования, записи, передачи и воспроизведения сигналов изображения и звука могут представлять собой весьма длинные цепи устройств. Например, получаемый с помощью микрофона сигнал - электрический аналог звука - проходит через различные усилительные устройства. Он может записываться с помощью многоканального магнитофона. Каждая дорожка первичной записи обрабатывается поразному. Сигнал подвергается частотной фильтрации, шумоподавлению, сжатию динамического диапазона, реверберации и т.п. Число преобразований сигнала изображения, которые нужно сделать в процессе формирования, записи, монтажа и передачи телевизионной программы, также очень велико. Каждое из звеньев систем выполняет свою полезную функцию, но при этом вносит искажения и помехи. При аналоговых методах обработки сигналов эти помехи накапливаются от звена к звену. Пока количество звеньев не велико, суммарные искажения могут быть незаметны. Но с развитием звукотехники и телевидения число необходимых преобразований сигнала быстро возрастает, что затрудняет разрешение проблемы помехоустойчивости. Накопление искажений в аналоговых системах, в конечном счете, ставит предел расширению функциональных возможностей аппаратуры.
Существенно уменьшить искажения, заменить слабые звенья и расширить функциональные возможности звукотехнической и видеотехнической аппаратуры позволяет внедрение цифровых методов записи, обработки и передачи сигналов.
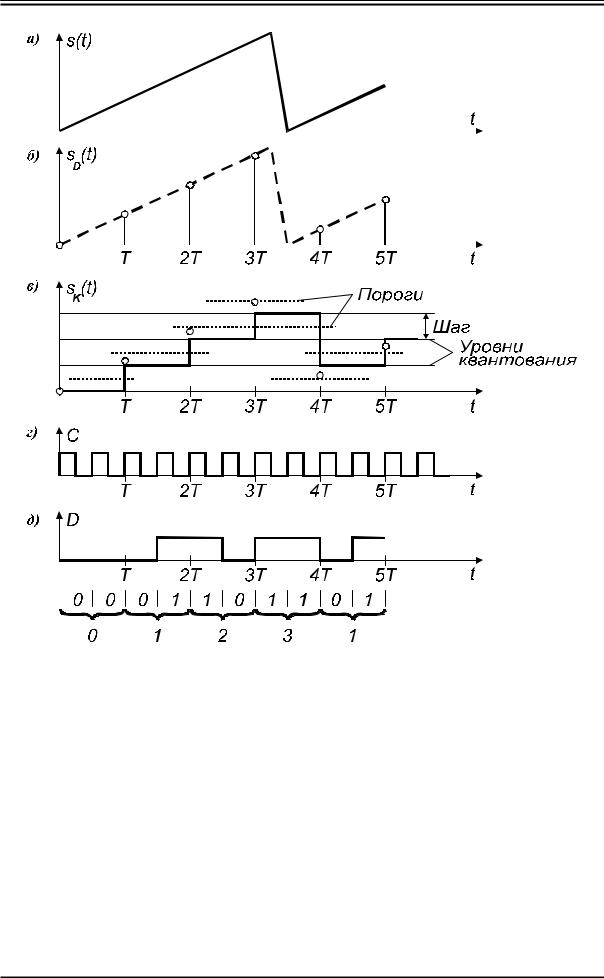
Для преобразования сигнала из аналоговой формы представления в цифровую необходимо выполнить ряд операций, основными из которых являются дискретизация, квантование и кодирование (рис.В.1).
Дискретизация - это представление непрерывного сигнала последовательностью своих значений (отсчетов) в дискретные моменты времени. Промежуток времени между соседними отсчетами времени называется интервалом дискретизации TD, а величина ему обратная – частотой дискретизации FD. Интуитивно ясно, что отсчеты должны следовать достаточно часто. Рассчитать интервал дискретизации позволяет теорема Котельникова. Эта теорема утверждает, что любой непрерывный сигнал с ограниченным по частоте спектром может быть точно восстановлен по своим отсчетам, если частота дискретизации, по крайней мере, в два раза превышает граничную частоту спектра.
4 |
Рис. В.1. Аналого-цифровое преобразование: |
а – аналоговый сигнал; б – дискретизированный сигнал;
в – квантованный сигнал;
г– тактовые импульсы; д – цифровой сигнал
Квантование представляет собой замену полученных отсчетов ближайшими значениями из набора фиксированных величин, называемых уровнями квантования. Уровни квантования делят весь диапазон возможного изменения значений отсчетов на конечное число интервалов - шагов квантования. Каждому уровню квантования соответствует определенная область отсчетов. Границы этой области определяются
ЦИФРОВЫЕ УСТРОЙСТВА И МИКРОПРОЦЕССОРЫ. ЧАСТЬ 1

5 |
ВВЕДЕНИЕ |
|
|
|
|
порогами квантования. Возникающие в процессе квантования искажения сигнала называют шумом квантования.
Квантованный сигнал в отличие от исходного (аналогового) может принимать только конечное число значений. Это позволяет представить его в пределах каждого интервала дискретизации числом, равным, например, порядковому номеру уровня квантования. Число это может быть выражено комбинацией некоторых знаков или символов.
Совокупность знаков (символов) и система определенных правил, при помощи которых информация может быть представлена в виде набора из таких символов, называется кодом. Конечная последовательность кодовых знаков называется словом.
Квантованный сигнал можно преобразовать в последовательность кодовых слов, каждое из которых передается в пределах одного интервала дискретизации. Эта операция называется кодированием.
Для кодирования сигналов звука и изображения наиболее широко применяют двоичный код. Если квантованный сигнал может принимать N значений, то число двоичных символов в каждой кодовой комбинации, т.е.
длина слова n ≥ log2 N. Обычно число уровней квантования кратно целой степени числа 2. Для передачи слова интервал дискретизации можно разделить на n тактов. Начало каждого такта определяется тактовыми импульсами. В пределах такта передается один символ слова. Один разряд или символ слова, представляющий двоичный код, называют битом.
Каждый символ слова передается с помощью одного или нескольких дискретных сигналов, например, импульсов. Форма представления исходного кода определенными сигналами называется форматом кода. Можно, например, устанавливать в пределах такта высокий уровень сигнала, если в данном такте передается символ "1", и низкий (нулевой), если передается символ "0". Такой способ представления называют форматом БВН (без возвращения к нулю). Этот формат отражает режим работы логических схем.
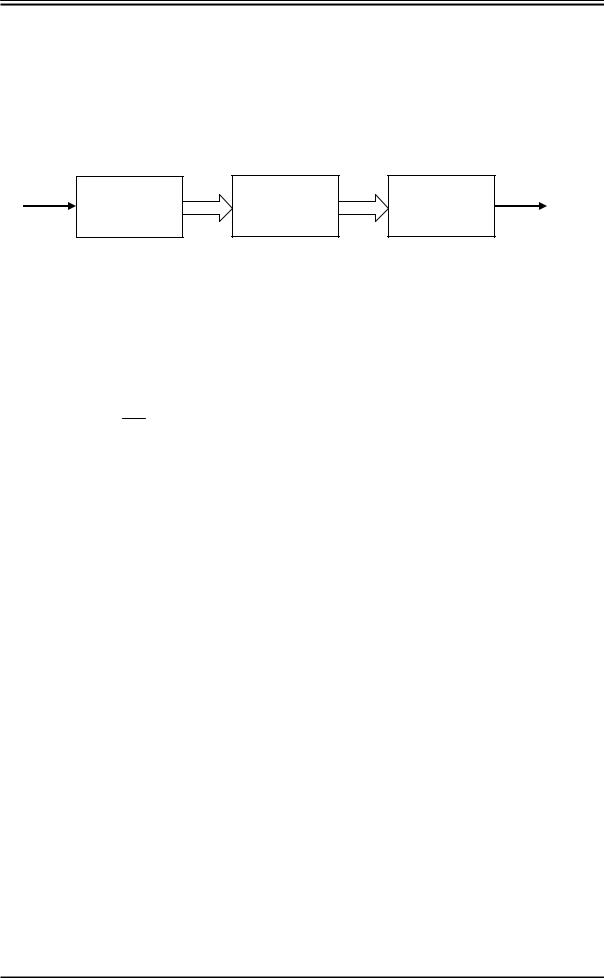
Временная диаграмма рис.В.1д показывает сигнал в цифровой форме, или данные, представляющие информацию об исходном аналоговом сигнале в двоичном коде БВН (в данном примере длина кодового слова n = 2). Операции, связанные с преобразованием аналогового сигнала в цифровую форму (дискретизация, квантование и кодирование), выполняются одним устройством - аналого-цифровым преобразователем (АЦП). Обратная операция, т.е. превращение цифрового сигнала в аналоговый, производится в цифро-аналоговом преобразователе (ЦАП). АЦП и ЦАП входят в состав любой системы цифровой обработки сигналов звука и изображения. Обобщенная схема системы цифровой обработки сигналов звука и изображения показана на рис.В.2. Входной и выходной
6
сигналы являются аналоговыми. Цифровой процессор осуществляет обработку сигнала, представленного в цифровой форме. Алгоритм обработки может быть описан в виде последовательности некоторых вычислительных операций. Обработка в процессоре сводится к такому преобразованию данных, при котором результирующий сигнал численно равен итогу соответствующих вычислительных операций.
АЦП |
Цифровой |
ЦАП |
|
процессор |
|||
|
|
Рис. В.2. Обобщенная схема системы цифровой обработки сигналов.
Важным показателем цифровых систем является скорость передачи данных. Если длина слова равна n , а частота дискретизации:
FD = T1 ,
D
то скорость передачи данных, выраженная в числе двоичных символов в секунду (бит/с), находится так:
C = |
n |
= n FD . |
|
||
|
TD |
|
В системах цифровой передачи речевых сигналов (в телефонии) используется частота дискретизации 8 кГц. Максимальная частота передаваемого сигнала не превышает 4 кГц, что вполне достаточно для обеспечения разборчивости речи. Длина кодового слова - n =8 , что означает квантование на 256 уровней. Скорость передачи данных в таких системах C = 64 кбит/с.
Для обеспечения высокого качества звуковоспроизведения цифровой сигнал, записанный на компакт-дисках лазерных проигрывателей, квантуется на 50 000 уровней (длина слова n =16 ) с частотой дискретизации около 40 кГц. Скорость передачи равна 640 кбит/с.
Сигнал изображения в цифровом телевидении дискретизируется с частотой 13,5 МГц при 256 уровнях квантования (кодовое слово имеет длину n =8 ). Скорость передачи данных весьма высока - 108 Мбит/с. Для передачи информации в цвете она должна быть удвоена.
Цифровые системы достаточно сложны в реализации. Но перспективность их внедрения в звукотехнику и видеотехнику
ЦИФРОВЫЕ УСТРОЙСТВА И МИКРОПРОЦЕССОРЫ. ЧАСТЬ 1

7 |
ВВЕДЕНИЕ |
|
|
|
|
предопределена рядом преимуществ цифровых методов представления и обработки сигналов, из которых важнейшими являются следующие:
•возможность большого числа обработок цифрового сигнала, включая процессы монтажа и тиражирования, с сохранением высокого качества воспроизведения аналогового сигнала;
•повышения качества записи и передачи сигналов, благодаря значительному уменьшению накопления искажений (в сравнении с аналоговыми системами) и применением кодов с обнаружением и исправлением ошибок;
•высокая технологичность производства и возможность длительного бесподстроечного режима работы цифрового оборудования за счет применения методов автоматической диагностики неисправностей.

8
1.СИСТЕМЫ СЧИСЛЕНИЯ И КОДЫ
1.1.Системы счисления
Запись числа в десятичной системе счисления подразумевает представление его в виде многочлена по степеням числа 10. Например, число 1987 является многочленом:
1987 = 1 103 + 9 102 + 8 101 + 7 100
Для записи числа в десятичной системе счисления требуются 10 символов (от 0 до 9). В системе счисления с основанием положительное число А представляет собой многочлен
A = an−1 qn−1 +an−2 qn−2 +K+a0 q0 +a−1 q−1 +K+am qm
n−1 |
|
A = ∑ai qi , |
|
i=−m |
|
где q – целое число, большее 1; |
|
ai – целые числа в диапазоне 0 ≤ ai ≤ (q −1). |
|
Последовательность an−1 ,...,a0 образует целую |
часть числа А, а |
последовательность a−1,...,a−m – дробную часть А. |
n и m обозначают |
количество цифр в целой и дробной частях. Цифры an−1 и a−m называют старшими и младшими значащими разрядами.
Для выполнения операций над числами с помощью логических схем удобным является представление чисел в двоичной системе счисления, или в двоичном коде. При этом q = 2 и число представляет собой многочлен по степеням числа 2:
A = an−1 2n−1 +an−2 2n−2 +K+a0 20 +a−1 2−1 +K+am 2m
n−1
A = ∑ai 2i ,
i=−m
где ai принимает только два значения – 0 и 1.
Отдельные цифры в записи, представляющей собой двоичный код числа, называют битами. Кодовое слово длиной 8 бит называют байтом. Преобразование чисел из двоичной формы в десятичную осуществляется весьма просто. Двоичное число представляется в виде многочлена по
ЦИФРОВЫЕ УСТРОЙСТВА И МИКРОПРОЦЕССОРЫ. ЧАСТЬ 1

9 |
СИСТЕМЫ СЧИСЛЕНИЯ И КОДЫ |
|
|
|
|
степеням числа 2 и этот многочлен вычисляется с помощью десятичной арифметики. Например, число 1101,12 в десятичной системе счисления:
1101,12 = 1 23 + 1 22 + 0 21 + 1 20 + 1 2-1 = 13,510
Переход от десятичной формы к двоичной выполняется различным образом для целой и дробной частей числа. Целая часть десятичного числа (или целое число) переводится в двоичную форму путем последовательного деления на 2 и записи остатков. Остаток первого
деления образует младший двоичный разряд целой части a0 . Деление
продолжается до тех пор, пока частное не обратится в 0. Остаток от последнего деления равен старшему значащему разряду двоичного числа.
Старшая цифра дробной части двоичного числа a−1 может быть
найдена умножением дробной части десятичного числа на 2. Если это произведение меньше 1, то a =0, если же оно больше или равно 1, то a =1,
т.е. равна целой части произведения. Следующая цифра a−2 определяется путем умножения дробной части полученного ранее произведения на 2 и выделения его целой части и т.д. Этот процесс может быть бесконечным, так как не всегда конечная десятичная дробь может быть представлена конечной двоичной. Тогда процесс последовательного умножения прекращается при достижении необходимой точности.
Для компактной записи двоичных чисел часто используются восьмеричная и шестнадцатеричная форма представления. Преобразование чисел, записанных в двоичной и восьмеричной или в шестнадцатеричной системах счисления, могут выполняться достаточно просто. Это обусловлено тем, что основания восьмеричных и шестнадцатеричных систем представляют собой целые степени числа 2. Для того чтобы записать двоичное число в восьмеричной системе, надо разбить его на группы по 3 бита, начиная с двоичной запятой, и заменить каждую группу соответствующей восьмеричной цифрой:
1210 = 11002 = 001 1002 = 148
Обратное преобразование основано на том, что каждая цифра восьмеричного числа может быть представлена тремя двоичными разрядами.
Для записи двоичного числа в шестнадцатеричном коде исходное число разбивается на группы по 4 бита, начиная с двоичной запятой, и для каждой группы находится шестнадцатеричный эквивалент (величины от 10 до 15 обозначаются буквами латинского алфавита от А до F):
3010 =111102 = 0001 11102 = 1Е16 .

10
Шестнадцатеричная запись двоичного числа предпочтительнее восьмеричной, так как современные ЭВМ манипулируют словами длиной 8, 16 или 32 разряда, т.е. словами, длина которых кратна 4. В табл. 1.1 даны представления чисел от 0 до 15 в различных системах.
|
|
|
|
|
|
Таблица 1.1 |
|
|
Основание системы |
|
|
||
|
|
|
|
|
|
|
10 |
2 |
|
8 |
|
16 |
2-10 |
|
|
|
|
|
|
|
0 |
0000 |
|
0 |
|
0 |
0000 |
1 |
0001 |
|
1 |
|
1 |
0001 |
2 |
0010 |
|
2 |
|
2 |
0010 |
3 |
0011 |
|
3 |
|
3 |
0011 |
4 |
0100 |
|
4 |
|
4 |
0100 |
5 |
0101 |
|
5 |
|
5 |
0101 |
6 |
0110 |
|
6 |
|
6 |
0110 |
7 |
0111 |
|
7 |
|
7 |
0111 |
8 |
1000 |
|
10 |
|
8 |
1000 |
9 |
1001 |
|
11 |
|
9 |
1001 |
10 |
1010 |
|
12 |
|
A |
0001 0000 |
11 |
1011 |
|
13 |
|
B |
0001 0001 |
12 |
1100 |
|
14 |
|
C |
0001 0010 |
13 |
1101 |
|
15 |
|
D |
0001 0011 |
14 |
1110 |
|
16 |
|
E |
0001 0100 |
15 |
1111 |
|
17 |
|
F |
0001 0101 |
16 |
0001 0000 |
|
20 |
|
10 |
0001 0110 |
17 |
0001 0001 |
|
21 |
|
11 |
0001 0111 |
18 |
0001 0010 |
|
22 |
|
12 |
0001 1000 |
19 |
0001 0011 |
|
23 |
|
13 |
0001 1001 |
20 |
0001 0100 |
|
24 |
|
14 |
0010 0000 |
1.2 Двоично-десятичные коды
Большая часть данных, которые вводятся в вычислительные машины, обычно представлена в десятичной форме. Поэтому находят применение коды, в которых каждая десятичная цифра представлена группой двоичных разрядов.
Для раздельного представления 10 цифр в двоичной форме необходимо иметь 4 двоичных разряда. Так как для 4 разрядов возможны 16 комбинаций, из которых используются только 10, то можно построить большое число различных кодов. Наиболее широкое распространение получил способ кодирования, при котором каждая десятичная цифра представлена в двоичной системе счисления:
ЦИФРОВЫЕ УСТРОЙСТВА И МИКРОПРОЦЕССОРЫ. ЧАСТЬ 1

11 |
СИСТЕМЫ СЧИСЛЕНИЯ И КОДЫ |
|
|
|
|
8710 = 1000 01112-10
Такой код называют натуральным двоично-десятичным кодом (слово “натуральный” часто опускают). Его разряды имеют весовые коэффициенты 1, 2, 4, 8, 10, 20, 40, 80 и т.д.
Двоично-десятичный код обладает избыточностью. Его применение неэффективно с точки зрения полноты использования двоичных комбинаций. Но он очень удобен при вводе и выводе данных в десятичной форме.
1.3 Унитарный код
Унитарный n-разрядный код каждому числу m от 0 до (n - 1) ставит в соответствие кодовую комбинацию длиной n. Разряд комбинации, занимающий позицию с номером m, равен 1, остальные разряды равны 0. Такой код имеет также название "1 из n". Кодовые комбинации, представляющие числа от 0 до 9, приведены в таблице. 1.2.
Таблица 1.2
m |
X9 |
X8 |
X7 |
X6 |
X5 |
X4 |
X3 |
X2 |
X1 |
X0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
4 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
5 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
6 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
8 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
9 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
Унитарный код используется для представления данных при их вводе в цифровые устройства (например, с помощью клавиатуры) и при отображении результатов с помощью индикаторов.
1.4 Код Грея
Во многих практических приложениях, например, при аналоговом цифровом преобразовании сигналов, желательно использовать коды, в которых все последовательные кодовые комбинации отличаются друг от друга лишь одним разрядом. Такие коды называют циклическими.

12
Наиболее часто применяется циклический код Грея. Это обусловлено простотой процедуры перехода от двоичного числа к такому коду. Четырехразрядный код Грея приведен в табл. 1.3.
Таблица 1.3
Десятичное |
|
Код Грея |
|
|
Двоичный код |
|
|||
число |
g3 |
g2 |
|
g1 |
g0 |
b3 |
b2 |
b1 |
b0 |
|
|
||||||||
0 |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
1 |
2 |
0 |
0 |
|
1 |
1 |
0 |
0 |
1 |
0 |
3 |
0 |
0 |
|
1 |
0 |
0 |
0 |
1 |
1 |
4 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
0 |
5 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
6 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
0 |
7 |
0 |
1 |
|
0 |
0 |
0 |
1 |
1 |
1 |
8 |
1 |
1 |
|
0 |
0 |
1 |
0 |
0 |
0 |
9 |
1 |
1 |
|
0 |
1 |
1 |
0 |
0 |
1 |
10 |
1 |
1 |
|
1 |
1 |
1 |
0 |
1 |
0 |
11 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
1 |
12 |
1 |
0 |
|
1 |
0 |
1 |
1 |
0 |
0 |
13 |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
1 |
14 |
1 |
0 |
|
0 |
1 |
1 |
1 |
1 |
0 |
15 |
1 |
0 |
|
0 |
0 |
1 |
1 |
1 |
1 |
Пустьgn−1 gn−2 ...g2 g1 g0 |
- кодовое слово в коде Грея с n разрядами, а |
||||||||
bn−1bn−2 ...b2b1b0 - соответствующее двоичное число, где индексы 0 и ( n −1)
обозначают младший и старший разряды соответственно. Тогда разряды кода Грея выражаются через биты двоичного числа следующим образом:
gn−1 = bn−1 ; gi = bi bi+1 ; 0 ≤ i ≤ n −2,
где - символ операции Исключающее ИЛИ:
0 0 = 0; 0 1 = 1; 1 0 = 1; 1 1 = 0.
Для определения бита bi при преобразовании кода Грея в двоичное число необходимо найти количество единиц в разрядах gi+1 − gn+1 . Если число единиц четно, то bi = gi , если нечетно – то bi = gi .
1.5 Код Джонсона
Кодовые комбинации кода Джонсона (табл. 1.4) отличаются друг от друга только в одном разряде. Он известен также под названием
ЦИФРОВЫЕ УСТРОЙСТВА И МИКРОПРОЦЕССОРЫ. ЧАСТЬ 1

13 |
СИСТЕМЫ СЧИСЛЕНИЯ И КОДЫ |
|
|
|
|
заполняющего кода. Это название связано с тем, что разряды кода, первоначально равные нулю, последовательно "заполняются" сначала единицами, а затем нулями (начиная с младшего разряда).
|
|
|
|
|
Таблица 1.4 |
|
m |
X4 |
X3 |
X2 |
X1 |
X0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
0 |
0 |
1 |
|
2 |
0 |
0 |
0 |
1 |
1 |
|
3 |
0 |
0 |
1 |
1 |
1 |
|
4 |
0 |
1 |
1 |
1 |
1 |
|
5 |
1 |
1 |
1 |
1 |
1 |
|
6 |
1 |
1 |
1 |
1 |
0 |
|
7 |
1 |
1 |
1 |
0 |
0 |
|
8 |
1 |
1 |
0 |
0 |
0 |
|
9 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
Код Джонсона легко преобразуется в унитарный код "1 из 10" по значениям двух разрядов, находящихся на границе "волн нулей" и "волн
единиц" (для m=0 и m=5 такими пограничными разрядами являются x0 и x4 ):
y0 = x0 x4 |
y5 = x0 x4 |
||
y1 = x0 x1 |
y6 |
= x0 x1 |
|
y2 |
= x1 x2 |
y7 |
= x1 x2 |
y3 = x2 x3 |
y8 |
= x2 x3 |
|
y4 |
= x3 x4 |
y9 |
= x3 x4 |
здесь y - разряды кода "1 из 10".
В таком пятиразрядном коде работают десятичные счетчики Джонсона.
1.6 Представление чисел со знаком
Существует несколько способов представления положительных и отрицательных чисел, выраженных в двоичном коде. Один из них предполагает представление числа посредством знака и величины, причем бит знака занимает самый старший разряд. Остальные разряды отводятся

14
для представления абсолютной величины числа. Если оно положительное, бит знака S равен 0, если оно отрицательное, то этот бит, равен 1. Такая форма представления определяет код числа:
[А]ПК = [± аn −1 Ka1 a0 ]ПК |
= S an −1 Ka1 a0 |
0 a |
n −1 |
Ka a |
, |
если А≥ 0; |
= |
1 0 |
|
если А≤ 0; |
|||
|
|
1 аn −1 Ka1 a0 , |
||||
где an−1...a1a0 - последовательность, представляющая в двоичном коде абсолютную величину n -разрядного числа.
Прямой код используется при выводе чисел на индикацию, при вводе данных, но он плохо подходит для вычислений. В нем существуют нули в двух формах (+0 и -0, определяемые соответственно как 0000 и 1000). При четырех разрядах, отведенных для представления числа, в прямом коде могут быть выражены числа от -7 до +7 включительно (таблица 1.5).
|
|
|
Таблица 1.5 |
Число |
Прямой код |
Код со смещением |
Дополнительный |
|
|
|
код |
-8 |
- |
0000 |
1000 |
-7 |
1111 |
0001 |
1001 |
-6 |
1110 |
0010 |
1010 |
-5 |
1101 |
0011 |
1011 |
-4 |
1100 |
0100 |
1100 |
-3 |
1011 |
0101 |
1101 |
-2 |
1010 |
0110 |
1110 |
-1 |
1001 |
0111 |
1111 |
0 |
0000 |
1000 |
0000 |
1 |
0001 |
1001 |
0001 |
2 |
0010 |
1010 |
0010 |
3 |
0011 |
1011 |
0011 |
4 |
0100 |
1100 |
0100 |
5 |
0101 |
1101 |
0101 |
6 |
0110 |
1110 |
0110 |
7 |
0111 |
1111 |
0111 |
Числа со знаком могут также быть представлены в коде со смещением. Последовательность всех чисел в коде со смещением, начиная со старшего отрицательного и кончая старшим положительным, представляет собой двоичную арифметическую прогрессию. Для получения кодовой комбинации какого-либо числа нужно прибавить к
нему число, равное 2n (здесь (n+1) число разрядов кодового слова), и представить результат в двоичном коде. Старшее отрицательное число имеет код 0000, а самое большое положительное - 1111 (см. табл. 1.5). Нуль в этом коде имеет однозначное представление. Коды положительных
ЦИФРОВЫЕ УСТРОЙСТВА И МИКРОПРОЦЕССОРЫ. ЧАСТЬ 1

15СИСТЕМЫ СЧИСЛЕНИЯ И КОДЫ
иотрицательных чисел отличаются старшим разрядом. Используется код со смещением в аналого-цифровых и цифро-аналоговых преобразователях.
Наиболее удобен для выполнения арифметических операций с целыми числами дополнительный код (см. табл. 1.5). Положительные числа при этом способе представления записываются как числа в прямом коде. Для того чтобы получить кодовую комбинацию отрицательного числа, нужно образовать обратный код равного ему по модулю положительного числа и добавить к полученному результату единицу.
Обратный код A образуется следующим образом:
[А]ОК = [± аn −1 Ka1 a0 ]ОК |
= 0 an −1 Ka1 a0 , |
если А≥ 0; |
|
1 аn −1 Ka1 a0 , |
если А≤ 0; |
где ai - инверсия величины ai .
Прямой и обратный коды положительных чисел совпадают. Для отрицательных чисел:
аn −1Ka1 a0 =1K11−аn −1Ka1 a0 = (2n −1)−аn −1Ka1 a0 ,
т.е. сумма чисел каждого разряда прямого и обратного кода отрицательных чисел равна 1 (без учета знакового разряда).
Дополнительный код числа A записывается следующим образом:
[А]ДК = [± аn −1 Ka1 a0 |
]ДК |
|
0 a |
Ka a |
, |
|
если А≥ 0; |
|
= |
~n −1 |
~1 ~0 |
|
|
если А< 0; |
|||
|
|
|
|
1 аn −1 Ka1 a0 , |
|
|||
~ |
~ ~ |
= аn−1 Ka1 a0 +1 = 2 |
n |
−аn−1 Ka1 a0 . |
||||
где аn−1 Ka1 a0 |
|
|||||||
Если для представления числа отводится (n + 1) двоичных разрядов (n - для абсолютной величины и 1 - для знака), то в дополнительном коде
можно записать 2n+1 чисел: (2n-1) положительных, нуль и 2n отрицательных. Нуль в дополнительном коде представлен единственным образом, старший разряд несет информацию о знаке. Правило образования дополнительного кода обратимо. Если найти дополнительный код числа, представленного в дополнительном коде, то получится прямой код этого числа.
Арифметические операции в дополнительном коде выполняются весьма просто. Для того чтобы получить сумму двух чисел, надо сложить соответствующие разряды с учетом переноса. Все разряды, (включая знаковый) обрабатывается одинаково. Перенос из знакового разряда игнорируется. Для выполнения вычитания надо вычитаемое представить в дополнительном коде и сложить с уменьшаемым. Если сумма имеет 1 в

16
знаковом разряде, то она представляет собой отрицательное число. Если складываются числа одного знака, а сумма имеет другой знак, то в дополнительном коде происходит выход за пределы изображения чисел при данном числе разрядов, что эквивалентно ошибке. На это должен указывать специально формируемый признак.
1.7 Коды с обнаружением ошибок
При передаче, обработке и записи данных нельзя полностью исключить возможность появления ошибок, возникающих из-за сбоев в работе аппаратуры или помех, поэтому часто используются такие способы кодирования данных, при которых можно определять возникновение ошибок.
Простейший способ распознавания одиночной ошибки заключается в добавлении к информационным разрядам контрольного бита проверки на четность р (бит паритета). Этот бит можно формировать двумя способами. При первом способе в контрольный разряд записывается 0, если число единиц в информационном слове четное. Если число единиц нечетное, то в контрольный разряд записывается 1. При этом общее количество единиц в кодовом слове, включая контрольный разряд, всегда оказывается четным (четный паритет).
Второй способ предлагает такое формирование контрольного разряда, при котором общее количество единиц в кодовом слове является нечетным (нечетный паритет).
В табл. 1.6 приведен двоично-десятичный код с обнаружением единичной ошибки (контрольный разряд сформирован в соответствии с условием четного паритета). Единичная ошибка в кодовом слове приведет к тому, что паритет будет нарушен (количество единиц станет нечетным). Поэтому проверка кодового слова на четность (вместе с контрольным разрядом) позволяет зафиксировать ошибку. Может быть также обнаружено нечетное число ошибок, большее 1. При четном числе ошибок паритет сохраняется, и они не фиксируются.
Принцип обнаружения ошибок может быть также пояснен следующим образом. Из пяти двоичных разрядов можно образовать 32 кодовых комбинации. Но, используются в коде (табл. 1.6), т.е. являются допустимыми, только десять. Остальные кодовые комбинации являются недопустимыми. Как следует из табл.1.6, любые две допустимые комбинации отличаются друг от друга, по крайней мере, в двух разрядах. Поэтому единичная ошибка переводит допустимую комбинацию в недопустимую. Появление в потоке данных недопустимой кодовой комбинации и указывает на ошибку, т.е. позволяет ее обнаружить.
ЦИФРОВЫЕ УСТРОЙСТВА И МИКРОПРОЦЕССОРЫ. ЧАСТЬ 1

|
|
|
17 |
|
|
СИСТЕМЫ СЧИСЛЕНИЯ И КОДЫ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.6 |
|
|
|
|
|
|
|
|
|
|
|
|
Десятичная |
|
|
Кодовое слово |
|
|
|||
|
цифра |
d3 |
d2 |
|
d1 |
|
d0 |
|
p |
|
0 |
0 |
0 |
|
0 |
|
0 |
|
0 |
|
1 |
0 |
0 |
|
0 |
|
1 |
|
1 |
|
2 |
0 |
0 |
|
1 |
|
0 |
|
1 |
|
3 |
0 |
0 |
|
1 |
|
1 |
|
0 |
|
4 |
0 |
1 |
|
0 |
|
0 |
|
1 |
|
5 |
0 |
1 |
|
0 |
|
1 |
|
0 |
|
6 |
0 |
1 |
|
1 |
|
0 |
|
0 |
|
7 |
0 |
1 |
|
1 |
|
1 |
|
1 |
|
8 |
1 |
0 |
|
0 |
|
0 |
|
1 |
|
9 |
1 |
0 |
|
0 |
|
1 |
|
0 |
Число несовпадающих разрядов определяет кодовое расстояние между двумя словами. Минимальным кодовым расстоянием называется наименьшее число разрядов, в которых различаются любые две кодовые комбинации. Например, в двоичном, двоично-десятичном, дополнительных кодах минимальное расстояние равно 1. Искажение любого разряда приводит к ошибке, которую нельзя обнаружить. В коде, приведенном в табл. 1.6, минимальное расстояние равно 2. Очевидно, что код является кодом с обнаружением ошибок тогда и только тогда, когда его минимальное расстояние не меньше двух.
1.8 Коды с исправлением ошибок
Для того чтобы код позволял исправлять ошибки, необходимо увеличивать его минимальное расстояние. Если минимальное кодовое расстояние равно трем, то любая одиночная ошибка переводит допустимую кодовую комбинацию в недопустимую, находящуюся на расстоянии, равном единице от исходной комбинации, и на расстоянии, больше или равном двум от любой другой допустимой кодовой комбинации. Поэтому в коде с минимальным расстоянием, равном трем, можно исправить любую одиночную ошибку.
Рассмотрим основные принципы построения часто используемого кода Хэмминга, позволяющего исправлять одиночную ошибку. К каждой группе из m информационных разрядов, представляющих собой
сообщение, присоединяются k контрольных разрядов p1, p2,…, pk проверки на четность. Затем присваивают десятичный номер позиции каждого из (m + k) разрядов кодовой комбинации, начиная со значения 1 для старшего разряда и кончая значением (m + k) для младшего. Производится k проверок на четность числа единиц в выбранных разрядах каждой кодовой комбинации. Результат каждой проверки записывается в виде 0, если число единиц четное (ошибки нет), и в виде 1 , если число

18
единиц нечетное (произошла ошибка). По результатам проверки
составляется двоичное число c1, c2, … ck, десятичный эквивалент которого равен номеру позиции разряда, где произошла ошибка. Если это число равно 0, то ошибка отсутствует. После того, как обнаружен ошибочный разряд, его можно исправить путем инверсии.
Число контрольных разрядов можно определить следующим образом.
Используя k разрядов, можно задать 2k двоичных комбинаций. Нулевая комбинация указывает на отсутствие ошибки, десятичные эквиваленты остальных должны определять номера позиций любого из (m + k) разрядов. Следовательно, число k должно удовлетворять неравенству:
2k ≥ m + k + 1.
Из этого неравенства следует, что доля контрольных разрядов в общей длине кодовой комбинации тем меньше, чем больше число информационных разрядов.
Для того, чтобы контрольные разряды проверки на четность определять лишь через информационные разряды и независимо друг от
друга, их размещают в позициях 1, 2, ... 2k-1. На остальных позициях находятся биты, представляющего код исходного сообщения.
В табл. 1.7 и 1.8 показан пример построения кода Хэмминга при четырех информационных разрядах (m=4, k=3). Контрольные разряды должны задаваться так, чтобы номер позиции соответствовал положению ошибочного бита. Если ошибка появляется в позициях 1, 3, 5, 7, то
младший разряд номера позиции, т.е. c3 должен равняться единице. Если код построен так, то в каждой кодовой комбинации сумма битов в позициях 1, 3, 5, 7, четная и появление одиночной ошибки в любой из этих позиций приведет к нечетному числу единиц в указанных позициях. В этом случае младший разряд номера позиции принимается равным 1. Если
ошибки нет, то сума единиц в указанных позициях остается четной, и c3
полагается равным 0. Таким образом, p1 выбирается так, чтобы установить четное число единиц в позициях 1, 3, 5, 7. Рассуждая аналогичным
образом, нетрудно прийти к выводу, что p2 выбирается так, чтобы четным
было число единиц в позициях 2, 3, 6, 7, а p3 должен обеспечить четность числа единиц в позициях 4, 5, 6, 7.
ЦИФРОВЫЕ УСТРОЙСТВА И МИКРОПРОЦЕССОРЫ. ЧАСТЬ 1

|
|
|
|
|
19 |
|
|
СИСТЕМЫ СЧИСЛЕНИЯ И КОДЫ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.7 |
||
|
Номера позиций |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Позиция ошибки |
|
|
|
Номер позиции |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
c1 |
|
c2 |
|
|
|
c3 |
|||||
|
|
|
|
|
|
|
|
|
|||||
|
0 (Ошибки нет) |
|
0 |
|
0 |
|
|
|
0 |
|
|||
|
1 |
|
|
|
0 |
|
0 |
|
|
|
1 |
|
|
|
2 |
|
|
|
0 |
|
1 |
|
|
|
0 |
|
|
|
3 |
|
|
|
0 |
|
1 |
|
|
|
1 |
|
|
|
4 |
|
|
|
1 |
|
0 |
|
|
|
0 |
|
|
|
5 |
|
|
|
1 |
|
0 |
|
|
|
1 |
|
|
|
6 |
|
|
|
1 |
|
1 |
|
|
|
0 |
|
|
|
7 |
|
|
|
1 |
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.8 |
||
|
Код Хемминга |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кодовое слово |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Десятичная |
p1 |
|
p2 |
d3 |
|
p3 |
|
d2 |
d1 |
|
d0 |
|
|
цифра |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Позиция |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
0 |
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
1 |
1 |
|
1 |
0 |
|
1 |
|
0 |
|
0 |
|
1 |
|
2 |
0 |
|
1 |
0 |
|
1 |
|
0 |
|
1 |
|
0 |
|
3 |
1 |
|
0 |
0 |
|
0 |
|
0 |
|
1 |
|
1 |
|
4 |
1 |
|
0 |
0 |
|
1 |
|
1 |
|
0 |
|
0 |
|
5 |
0 |
|
1 |
0 |
|
0 |
|
1 |
|
0 |
|
1 |
|
6 |
1 |
|
1 |
0 |
|
0 |
|
1 |
|
1 |
|
0 |
|
7 |
0 |
|
0 |
0 |
|
1 |
|
1 |
|
1 |
|
1 |
|
8 |
1 |
|
1 |
1 |
|
0 |
|
0 |
|
0 |
|
0 |
|
9 |
0 |
|
0 |
1 |
|
1 |
|
0 |
|
0 |
|
1 |
Рассмотрим пример обнаружения положения ошибки и ее исправления. Пусть, например, передана кодовая комбинация 1101001 (сообщение - число 1), но из-за ошибки принято слово 1101101. Проверка
на четность в позициях 4, 5, 6, 7 дает с1=1. В позициях 2, 3, 6, 7 число единиц четное, поэтому с2=0. Проверка числа единиц в позициях 1, 3, 5, 7
обуславливает с3=1. Получен номер 101, что означает ошибку в пятой позиции. Инверсия пятого разряда позволяет получить правильное кодовое слово.
20
Минимальное расстояние построенного кода Хэмминга равно трем. Следовательно, он позволяет исправить только одиночную ошибку. Ненулевая вероятность одиночной ошибки в кодовом слове существует в любой цифровой аппаратуре. Вероятность возникновения двух и более ошибок значительно меньше. Поэтому код Хэмминга имеет большое значение. Он часто применяется при передаче и записи данных для защиты информации.
1.9 Форматы кодов
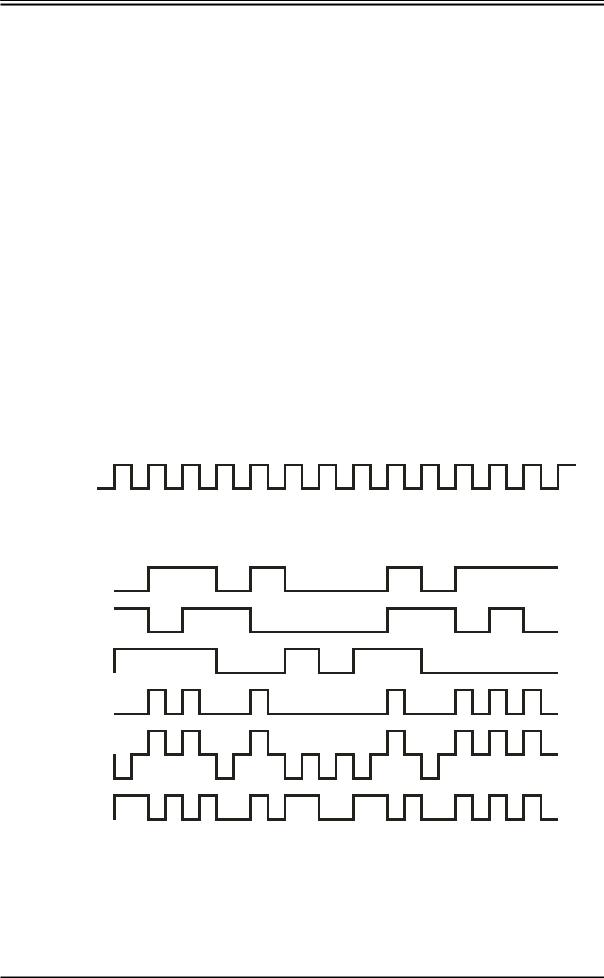
Каждый бит кодового слова передается или записывается с помощью дискретных сигналов, например, импульсов. Как было отмечено выше, способ представления исходного кода определенными сигналами определяется форматом кода. Известно большое количество форматов, каждый из которых имеет свои достоинства и недостатки и предназначен для использования в определенной аппаратуре. Часто используемые форматы приведены на рис. 1.1. Первая диаграмма рисунка показывает тактовые импульсы C, вторая - последовательность битов D, определяющая кодовое слово данных. Остальные диаграммы иллюстрируют представление исходного кода в различных форматах.
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
БВН БВН-1
БВН-0
ВН ВН-П
ДФ-0
Рис.1.1. Форматы кодов.
Формат БВН (без возвращения к нулю) естественным образом соответствует режиму работы логических схем. Единичный бит передается
ЦИФРОВЫЕ УСТРОЙСТВА И МИКРОПРОЦЕССОРЫ. ЧАСТЬ 1

21 |
СИСТЕМЫ СЧИСЛЕНИЯ И КОДЫ |
|
|
|
|
высоким уровнем напряжения (или тока), нулевой – низким уровнем. В пределах такта уровень не меняется. Положительный перепад означает переход из 0 к 1 в исходном коде, отрицательный - от 1 к 0. Отсутствие перепадов показывает, что значения предыдущего и последующего битов равны. Для декодирования кодов в формате БВН необходимы тактовые импульсы, так как в его спектре не содержится тактовая частота. Соответствующий коду формата БВН сигнал содержит низкочастотные компоненты (при передаче длинных серий нулей или единиц перепады не возникают).
Формат БВН-1 (без возвращения к нулю с перепадом при передаче 1) является разновидностью формата БВН. В отличие от последнего в БВН-1 уровень не передает данные, так как и положительные и отрицательные перепады соответствуют единичным битам. Перепады сигнала формируются при передаче 1. При передаче 0 уровень не меняется. Для декодирования требуются тактовые импульсы.
Формат БВН -0 (без возвращения к нулю с перепадом при передаче 0) является дополнительным к БВН-1 (перепады соответствуют нулевым битам исходного кода). В многодорожечных системах записи цифровых сигналов вместе с кодом в формате БВН надо записывать тактовые импульсы. Возможным вариантом является запись двух дополнительных сигналов, соответствующих кодам в форматах БВН-1 и БВН-0. В одном из двух сигналов перепады происходят в каждом такте, что позволяет получить импульсы тактовой частоты.
Формат ВН (с возвращением к нулю) требует передачи импульса, занимающего только часть тактового интервала (например, половину), при одиночном бите. При нулевом бите импульс не формируется.
Формат ВН-П (с активной паузой) означает передачу импульса положительной полярности при единичном бите и отрицательной - при нулевом бите. Сигнал этого формата имеет в спектре компоненты тактовой частоты. Он применяется в ряде случаев для передачи данных по линиям связи.
Формат ДФ-0 (двухфазный со скачком фазы при передачи 0) соответствует способу представления, при котором перепады формируются в начале каждого такта. При единичных битах сигнал в этом формате меняется с тактовой частотой, т.е. в середине каждого такта происходит перепад уровня. При передаче нулевого бита перепад в середине такта не формируется, т.е. имеет место скачок фазы. Код в данном формате обладает возможностью самосинхронизации и не требует передачи тактовых сигналов.
Направление перепада при передаче сигнала единицы не имеет значения. Поэтому изменение полярности кодированного сигнала не влияет на результат декодирования. Он может передаваться по

22
симметричным линиям без постоянной составляющей. Это также упрощает его магнитную запись. Этот формат известен также под названием "Манчестер 1". Он используется в адресно-временном коде SMPTE, широко применяющемся для синхронизации носителей звуковой и видеоинформации.
ЦИФРОВЫЕ УСТРОЙСТВА И МИКРОПРОЦЕССОРЫ. ЧАСТЬ 1
