2.4. Обучающий алгоритм для нечёткого контроллера.

При обучении данной сети выделяются две фазы. В первой фазе происходит локальная инициализация членов функции и представленных правил. Во многих задачах эту фазу может выполнить эксперт, имеющий знания по правилам работы поставленной задачи. Он также может задать начальные приблизительные значения функций принадлежности [5]. Во второй фазе применяется супервизорная обучающая схема для оптимального выравнивания членов функций для желаемых выходов.

Организующая фаза. Задача для организующей обучающей фазы 1 может быть сформулирована так: подаются обучающие данные x_i(t), i=1, ... , n. Требуемый выходной уровень y_i(t), i=1, ... , m. Нечеткие области и. Нам необходимы локальные члены функций и нечеткие логические правила. В этой фазе сеть работает двухсторонним способом, узлы и связи в режимеup - down. Таким образом, обучающие входные и выходные данные подаются в сеть с двух сторон.

Сначала центры и ширины функций принадлежности определяются самоорганизующимися обучающимися правилами аналогично статистической организации. Это служит для эффективного распределения ресурсов сети благодаря размещению доменов членов функций только вокруг тех регионов пространства входов и выходов, где присутствуют данные. Здесь алгоритм Кохонена адаптирован для нахождения центра m_i функции принадлежности:

для

где a(t) - монотонно убывающая скалярная скорость обучения и Эти адаптивные формулы выполняются независимо для каждой входной и выходной лингвистической переменной. Определение какой изm_i является m_closed может быть выполнено через определенное время по схеме “Победитель получает все”.

Найдем центры функций, их ширины могут быть определены с помощью эвристического метода N -ближайших связей минимизацией следующей функции, которая относится к ширине s_i как:

где r - параметр перекрытия. Наша вторая обучающая фаза теперь сможет оптимально приспосабливать центры и ширины функций принадлежности. Ширина на этой стадии может быть, определена по эвристическому методу “первой ближайшей связи” так:

Используя различные законы соревновательного обучения происходит оптимизация связей между слоями. После такого обучения производится оценка весов различных узлов. Если вес очень мал, то связь с этим весом удаляется. Если у узла удалены все связи, то он также удаляется.

Обучающая фаза. После того, как найдены все нечеткие логические правила сеть стабилизируется и переходит во вторую обучающую фазу для оптимальной подгонки параметров членов функций. Цель второй фазы может быть, описана так: подается входная обучающая последовательность: x_i(t), i=1, ... , n. желаемый выходной уровень y_i(t), i=1,...,m, нечеткие области и, и нечеткие логические правила, необходимо оптимально подобрать параметры функций принадлежности. Нечеткие логические правила были определены на первой фазе или в некоторых задачах были даны экспертами, обладающими необходимыми знаниями. Пример последнего - эксперту нужно дать правила типа, если температура слишком высокая, то быстро ее снизить.

Во второй фазе задача минимизировать функцию ошибок

- желаемый выход

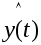- текущий выход.

Для каждой обучающей последовательности данных, начинающейся на входных узлах, проход вперед используется для вычисления уровня активности всех узлов в сети. Затем начинающийся на выходных узлах проход назад используется для вычисления для всех невидимых узлов (внутренних узлов).

Результирующим w - желаемый параметр узла. Главное используемое обучающее правило это:

где h - скорость обучения и

(5)

Произведем вычисление слой за слоем, начиная с выходных узлов (используем колоколобразную функцию принадлежности и желаемые параметры этих вычисленийm_i и s_i)

Слой 5: Используя (4) и (5) адаптивные правила, центр m_i ищется так:

Параметр центра обновляется как:

точно так же применим правила (4) и (5) для ширины s_i:

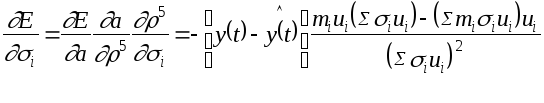
и параметр обновляется так:

Ошибка распространения в следующий уровень это:

Слой 4: Для этого уровня у нас нет желаемых параметров m_i и s_i . Мы можем вычислить и передать только сигнал ошибки (d_i⁴):

и из (2)

Сигнал ошибки:

Слой 3: Как и в слое четыре надо вычислить только сигнал ошибки. Согласно (3) этот сигнал может быть, вычислен так:

Таким образом, сигнал ошибки d_i³=d_i⁴ . Если у нас много выходов, то сигнал ошибки будет , где суммирование производится по последовательности узлов правил.

Слой 2: Используя (5) и (1) адаптивные правила m_ij вычисляется как:

где из предыдущего получили

и из (2)

Где суммирование выполняется по узлам правил, влияющих на a_i и

Итак, адаптивное правило m_ij:

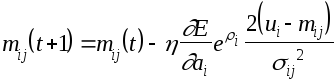
Точно также, используя (5) и (1) для s_ij получим:

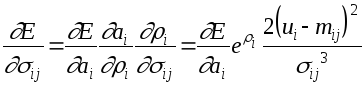
Адаптивное правило s_ij:

Скорость работы данного алгоритма намного выше, чем работа алгоритма обычной сети обратного распространения благодаря оптимизированной схеме сети и уменьшенному количеству вычислений.