Введение.

В настоящее время термин нечеткости все больше привлекает внимание специалистов из различных областей науки. Возрастание роли вычислительной техники в жизни людей связано с растущей потребностью человека в различного рода информации. Именно эта потребность все больше увеличивает роль компьютерных систем в нашей жизни. Но увеличение роли компьютеров в жизни человека выдвигает другую проблему, проблему общения человека и компьютера.

Современные компьютеры построены на четких математических правилах и они понимают только специальные четкие языки, которые строго математически описывают решение задачи и проблемы, которые вкладывает в него человек. Но с другой стороны в жизни самого человека, в его естественном языке, очень мало четких понятий, так как человек, как и знания его в большинстве областей нечетки. Такое различие между человеком и компьютером ограничивает решаемые компьютером задачи.

Четверть века назад Л.Заде предложил теорию нечетких множеств, позволяющую описывать нечеткие понятия и знания, оперировать этими знаниями и делать нечеткие выводы. Методология построения различных нечетких систем значительно расширила области применения компьютеров и более того, такие системы можно в принципе создавать практически в любой области деятельности человека.

Применение нечеткой логики эффективно в системах управления, математические модели которых неизвестны, очень сложны или изменяются во времени, для нелинейных или динамических процессов.

Идея нечеткого управления заключается в реализации с помощью программных или аппаратных средств качественного процесса решения задачи, при котором осуществляется обработка большого количества правил типа «если ... то». Однако в ряде случаев нечеткая логика может привести к значительному увеличению объема вычислений. Решением данной проблемы является применение нечетких нейросетевых структур, обладающая возможностью параллельного вычисления с высокой степенью гибкости и способностью к адаптации и обучению. Целью данной работы является разработка программного обеспечения для имитационного моделирования контроллера с нечеткой логикой на основе нейронной сети обратного распространения и анализ эффективности алгоритмов построения и обучения сетей данного типа.

Глава 1. Нейронечеткие методы вычислений

1.1. Основные положения метода нечеткого управления.

Идея нечеткого управления заключается в реализации качественного процесса решения задачи с использованием нечетких выводов. Другими словами, при нечетком управлении осуществляется параллельная обработка большого числа правил, составленных либо на основе нечеткой модели оборудования, либо на основе опыта и знаний эксперта.

Нечеткое управление основано на теории нечетких множеств. Понятие нечеткого множества является расширенным понятием, охватывающим и понятие четкого множества [3]. Для четких множеств принадлежность или непринадлежность элемента x к A описывается с помощью характеристической функции m_A(x), где

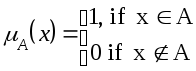
Теория нечетких множеств расширила данную концепцию путем введения функций принадлежности. Нечеткое множество A в полном пространстве X определяется через функцию принадлежности m_A(x) следующим образом

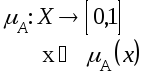
Таким образом, нечеткое множество строго определяется через функции принадлежности, т.е. логика определения понятия нечеткого множества не содержит в себе какой-либо нечеткости. Можно рассматривать различные операции над нечеткими множествами по аналогии с четкими [3]. Пусть A и B - два нечетких множества с функциями принадлежности m_A и m_B.

Дополнение нечеткого множества A - это нечеткое множество с функцией принадлежности

.

Сумма нечетких множеств - это нечеткое множество с функцией принадлежности

.

Произведение нечетких множеств - это множество с функцией принадлежности.

Нечеткие выводы, нечеткие и приближенные рассуждения - это наиболее важный метод в нечеткой логике. Рассмотрим простой пример выполнения нечетких выводов по правилам. Пусть существуют знания эксперта о том, что необходимо открыть спускной клапан, если уровень воды поднимется. Это знание представим с помощью нечеткого продукционного правила типа “если ... то ...”:

Если уровень воды высокий, то открыть клапан.

Здесь выражение, стоящее после если, называется предпосылкой, условием и т.п., а выражение, стоящее после то, - заключением, операцией и т.п. Необходимо описать предпосылку и заключение в виде нечеткого отношения. Интерпретацию знаний эксперта с помощью нечеткого множества можно сделать следующим образом:

ВЫСОКИЙ = 0,1/1,5 м + 0,3/1,6 м + 0,7/1,7 м + 0,8/1,8 м + 0,9/1,9 м + 1,0/2,0 м + 1,0/2,01 м + 1,0/2,2 м.

Аналогично угол поворота клапана, если принять 90° за полное открытие, можно описать с помощью следующей функции принадлежности:

ОТКРЫТЬ = 0,1/30° + 0,2/40° + 0,3/50° + 0,5/60° + 0,8/70° + 1,0/80° + 1,0/90°.

Человек, проектирующий данную систему, создает из правил в словесном представлении конкретные функции принадлежности. Какие же вычисления нужно проделать в программе или внутри специальной микросхемы нечеткого вывода, где встроены функции принадлежности? Существует более ста методов преобразования нечетких выводов на лингвистическом уровне в вычисления. Наиболее часто используемый метод - это метод нахождения центра тяжести композиции максимум-минимум. Можно также применять для дефадзификации метод меридианы, метод весов и т.д. Кроме того, на теоретическом уровне изучаются другие методы преобразований, другие разновидности нечетких выводов.

Рассмотрим метод построения нечеткой модели системы на примере нечеткого контроллера Сугено [2]. Нечеткая модель представляется в виде множества логических правил

,

где L_j означает j-е правило, A₁^j,B^j - нечеткие множества, x_i - входные переменные ,y_j - выходное значение j-го правила.

Окончательный результат вывода получается как средневзвешенное значение всех выводов для каждого правила с использованием в качестве весов значений истинности правил:

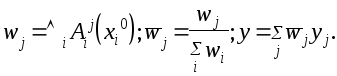
Обычно в нечетких контроллерах для Ù используют оператор минимума:

Ключевым моментом качественного моделирования является идентификация нечеткой модели системы. Построение нечеткой модели обычно состоит из двух аспектов: структурной идентификации и параметрической идентификации [2]. Структурная идентификация системы решает две задачи: определение входных переменных (тип 1) и определение отношений типа вход-выход (тип 2). На этапе параметрической идентификации определяют величины параметров системной модели. Для нечеткой модели это функции принадлежности. Идентификация модели - это один из важнейших этапов нечеткого управления, так как от правильного определения функциональной глобальной структуры системы и результатов создания нечеткой модели зависит конечная работа нечеткого контроллера.

В условиях больших изменений внешних условий при производстве ИМС возможны случаи, когда трудно получить оптимальные результаты даже при управлении с помощью нечеткого контроллера. В подобных ситуациях возникает потребность реализации в нечеткой системе функций обучения и самонастройки, позволяющих настраивать параметры нечеткого контроллера по оценкам реакции на управляющие воздействия. Современное производство ИМС выдвигает жесткие требования к мобильности и гибкости производственных процессов и таким системным параметрам, как стоимость, качество, сроки изготовлеия. При этом возникает необходимость в решении таких прикладных задач, как обработка неполной и нечеткой информации, автоматическое управление процессами в реальном времени, разработка средств принятия решений и оценки режимов работы и т.д. Для решения этих задач можно с успехом воспользоваться достоинствами нечеткой логики и ее особенностями.