
- •Содержание.
- •Введение.
- •Глава 1. Нейронечеткие методы вычислений
- •1.1. Основные положения метода нечеткого управления.
- •1.2. Нейронные сети в системах контроля и управления.
- •Глава 2. Алгоритм реализации нечёткого контроллера на основе сетей обратного распространения.
- •2.1. Нейронные сети с обратным распространением ошибки.
- •2.2. Алгоритм обучения с обратным распространением ошибки.
- •2.3. Алгоритм работы нечёткого контроллера.
- •2.4. Обучающий алгоритм для нечёткого контроллера.
- •Глава 3. Методы управления в компьютерно-интегрированном производстве.
- •3.1. Компьютерно-интегрированное производство.
- •3.2. Типовой технологический маршрут изготовления кмоп ис
- •Глава 4. Реализация программного обеспечения и результаты имитационного моделирования алгоритма нечёткого контроллера.
- •4.1. Реализация алгоритма нечёткого контроллера высокотемпературных операций.
- •Результаты имитационного моделирования.
- •4.3. Вывод.
- •Глава 5. Сегментация рынка контроллеров на основе нейронных сетей.
- •5.1. Общие положения.
- •5.2. Методика расчёта сегментации рынка.
- •5.3. Поиск сегментов рынка нечётких контроллеров.
- •5.4. Вывод.
- •Глава 6. Электробезопасность в помещениях вычислительных центров.
- •6.1. .Анализ вредных воздействий на организм человека при работе на эвм.
- •6.2. Электроопасность при работе с эвм.
- •6.3. Факторы влияющие на степень поражения электрическим током.
- •6.4. Медицинская помощь при поражении электрическим током.
- •6.5. Организационные и Технические мероприятия по безопасности эксплуатации.
- •6.6. Вывод.
- •Заключение.
- •Литература.
- •Глава 1-6.
- •Глава 7.
- •Глава 6.
- •Приложение.
Результаты имитационного моделирования.
Целью имитационного моделирования была задача определить и сравнить время и скорость обучения обычной нейроподобной сети обратного распространения и оптимизированной сети обратного распространения. Моделирование для нечеткого контроллера, управляющего технологическим этапом высокотемпературной обработки пластин.
Компьютерное моделирование процесса обучения сети обратного распространения должно иллюстрировать стремление выходных векторов к заданным тестовым значениям. Тестовые данные для обучения нейронной сети получены с помощью программы моделирования TMA TSUPREM4 (компьютерная программа моделирования технологических процессов в производстве кремниевых интегральных схем и отдельных приборов). Расчеты проводились на рабочей станции SUN SPARCstation 10.
Обучающие примеры рассчитаны для формирования N- и , n+- и p+- истока/стока в МДП транзисторе (ионное легирование + разгонка). Взят простой вариант термодиффузионной операции: один отрезок времени + равномерная температура + одна среда. В таблице 4.1 представлены обучающие вектора для области p+- стока /истока
Таблица 4.1
Тестовые данные для обучения (p+- сток /исток)
Исходная структура: КЭФ - 4,5
|
|
Входные параметры |
Выходные параметры | ||||||
|
№ |
Энергия keV |
Доза см-2 |
Примесь |
rS Ом/кв |
xj Ом/кв |
Время, мин |
Тем-ра 0С |
Среда |
|
1 |
20 |
1015 |
Бор |
214 |
0.4999 |
10 |
850 |
О2 |
|
2 |
|
|
|
209 |
0.4999 |
15 |
850 |
|
|
3 |
|
|
|
204 |
0.4999 |
20 |
850 |
|
|
4 |
|
|
|
199 |
0.4999 |
25 |
850 |
|
|
5 |
|
|
|
195 |
0.4999 |
30 |
850 |
|
|
6 |
|
|
|
151 |
0.5011 |
15 |
900 |
|
|
7 |
|
|
|
153 |
0.5020 |
25 |
900 |
|
|
8 |
|
|
|
157 |
0.5029 |
35 |
900 |
|
|
9 |
|
|
|
145 |
0.5701 |
15 |
1000 |
|
|
10 |
|
|
|
148 |
0.5893 |
20 |
1000 |
|
|
11 |
|
|
|
150 |
0.6341 |
25 |
1000 |
|
|
12 |
20 |
2*1015 |
Бор |
118 |
0.5223 |
10 |
900 |
О2 |
|
13 |
|
|
|
101 |
0.5220 |
20 |
900 |
|
|
14 |
|
|
|
90 |
0.5218 |
30 |
900 |
|
|
15 |
|
|
|
84 |
0.5234 |
40 |
900 |
|
|
16 |
|
|
|
78 |
0.5228 |
5 |
950 |
|
|
17 |
|
|
|
76 |
0.5315 |
15 |
950 |
|
|
18 |
|
|
|
79 |
0.5593 |
25 |
950 |
|
|
19 |
|
|
|
70 |
0.5270 |
3 |
1000 |
|
|
20 |
|
|
|
72 |
0.5665 |
8 |
1000 |
|
|
21 |
|
|
|
73 |
0.5922 |
12 |
1000 |
|
|
22 |
20 |
2*1015 |
Бор |
96 |
0.5241 |
20 |
900 |
N2 |
|
23 |
|
|
|
84 |
0.5248 |
30 |
900 |
|
|
24 |
|
|
|
79 |
0.5256 |
35 |
900 |
|
|
25 |
|
|
|
68 |
0.5352 |
15 |
900 |
|
|
26 |
5 |
1015 |
Бор |
190 |
0.3721 |
10 |
900 |
О2 |
|
27 |
|
|
|
184 |
0.3720 |
15 |
900 |
|
|
28 |
|
|
|
185 |
0.3718 |
20 |
900 |
|
|
29 |
|
|
|
152 |
0.3729 |
1 |
1000 |
|
|
30 |
|
|
|
143 |
0.3898 |
5 |
1000 |
|
|
31 |
|
|
|
144 |
0.4388 |
10 |
1000 |
|
|
32 |
5 |
5*1015 |
Бор |
349 |
0.4974 |
20 |
800 |
О2 |
|
33 |
|
|
|
345 |
0.4973 |
30 |
800 |
|
|
34 |
|
|
|
342 |
0.4972 |
40 |
800 |
|
|
35 |
|
|
|
149 |
0.4975 |
10 |
900 |
|
|
36 |
|
|
|
135 |
0.4975 |
15 |
900 |
|
|
37 |
|
|
|
122 |
0.4974 |
22 |
900 |
|
|
38 |
|
|
|
114 |
0.4975 |
28 |
900 |
|
|
39 |
|
|
|
58 |
0.5001 |
3 |
1000 |
|
|
40 |
|
|
|
43 |
0.5104 |
7 |
1000 |
|
|
41 |
|
|
|
31 |
0.5833 |
15 |
1000 |
|
|
42 |
10 |
1015 |
Бор |
270 |
0.3961 |
15 |
850 |
О2 |
|
43 |
|
|
|
261 |
0.3963 |
20 |
850 |
|
|
44 |
|
|
|
246 |
0.3968 |
30 |
850 |
|
|
45 |
|
|
|
160 |
0.4045 |
7 |
950 |
|
|
46 |
|
|
|
166 |
0.4157 |
15 |
950 |
|
|
47 |
|
|
|
167 |
0.4219 |
18 |
950 |
|
|
48 |
|
|
|
148 |
0.4054 |
2 |
1000 |
|
|
49 |
|
|
|
150 |
0.4207 |
5 |
1000 |
|
|
50 |
|
|
|
153 |
0.4449 |
10 |
1000 |
|
|
51 |
10 |
8*1014 |
Бор |
209 |
0.3817 |
10 |
900 |
О2 |
|
52 |
|
|
|
215 |
0.3856 |
20 |
900 |
|
|
53 |
|
|
|
223 |
0.3892 |
30 |
900 |
|
|
54 |
|
|
|
195 |
0.3865 |
5 |
950 |
|
|
55 |
|
|
|
207 |
0.4046 |
16 |
950 |
|
|
56 |
|
|
|
212 |
0.4201 |
22 |
950 |
|
|
57 |
|
|
|
185 |
0.4020 |
4 |
1000 |
|
|
58 |
|
|
|
193 |
0.4446 |
12 |
1000 |
|
|
59 |
35 |
4*1015 |
Бор |
114 |
0.8077 |
15 |
800 |
О2 |
|
60 |
|
|
|
114 |
0.8076 |
25 |
800 |
|
|
61 |
|
|
|
114 |
0.8075 |
32 |
800 |
|
|
62 |
|
|
|
93 |
0.8078 |
15 |
850 |
|
|
63 |
|
|
|
92 |
0.8074 |
20 |
850 |
|
|
64 |
|
|
|
91 |
0.8072 |
28 |
850 |
|
|
65 |
|
|
|
66 |
0.8075 |
10 |
900 |
|
|
66 |
|
|
|
64 |
0.8072 |
18 |
900 |
|
|
67 |
|
|
|
63 |
0.8072 |
20 |
900 |
|
|
68 |
|
|
|
43 |
0.8083 |
3 |
1000 |
|
|
69 |
|
|
|
34 |
0.8100 |
5 |
1000 |
|
|
70 |
|
|
|
35 |
0.8123 |
10 |
1000 |
|
|
71 |
35 |
1015 |
Бор |
178 |
0.6741 |
15 |
800 |
О2 |
|
72 |
|
|
|
177 |
0.6740 |
30 |
800 |
|
|
73 |
|
|
|
140 |
0.6742 |
10 |
850 |
|
|
74 |
|
|
|
133 |
0.6741 |
20 |
850 |
|
|
75 |
|
|
|
129 |
0.6740 |
30 |
850 |
|
|
76 |
|
|
|
129 |
0.6745 |
5 |
900 |
|
|
77 |
|
|
|
127 |
0.6750 |
15 |
900 |
|
|
78 |
|
|
|
130 |
0.6759 |
30 |
900 |
|
|
79 |
|
|
|
127 |
0.6761 |
5 |
950 |
|
|
80 |
|
|
|
128 |
0.6780 |
10 |
950 |
|
|
81 |
|
|
|
126 |
0.6793 |
3 |
1000 |
|
|
82 |
|
|
|
130 |
0.6914 |
10 |
1000 |
|
|
83 |
10 |
1015 |
Бор |
258 |
0.3972 |
20 |
850 |
N2 |
|
84 |
|
|
|
240 |
0.3980 |
30 |
850 |
|
|
85 |
|
|
|
351 |
0.3956 |
15 |
800 |
|
|
86 |
|
|
|
333 |
0.3960 |
40 |
800 |
|
|
87 |
|
|
|
158 |
0.4032 |
20 |
900 |
|
|
88 |
|
|
|
153 |
0.4087 |
35 |
900 |
|
|
89 |
|
|
|
136 |
0.4406 |
25 |
950 |
|
|
90 |
|
|
|
132 |
0.4446 |
8 |
1000 |
|
|
91 |
|
|
|
127 |
0.5199 |
15 |
1000 |
|
|
92 |
35 |
2*1015 |
Бор |
146 |
0.7398 |
20 |
800 |
N2 |
|
93 |
|
|
|
145 |
0.7399 |
35 |
800 |
|
|
94 |
|
|
|
74 |
0.7407 |
15 |
900 |
|
|
95 |
|
|
|
68 |
0.7417 |
30 |
900 |
|
|
96 |
|
|
|
65 |
0.7423 |
10 |
950 |
|
|
97 |
|
|
|
64 |
0.7459 |
25 |
950 |
|
|
98 |
|
|
|
63 |
0.7443 |
5 |
1000 |
|
Для отображения и сравнения результатов моделирования на экран дисплея выводится процесс изменения значений выходных векторов во время обучения. При сравнении результатов работы на экран выводится заданное значение выхода тестового вектора и рассчитанные сетью значения после ее обучения
Обычный алгоритм сети обратного распространения. Задачей моделирования данного алгоритма было обучение сети обратного распространения на один из сегментов тестового массива данных и получение временных зависимостей обучения сети в зависимости от количества подаваемых обучающих векторов. Временная зависимость использовалась для сравнения скорости обучения данного алгоритма и оптимизированного алгоритма сети обратного распространения.
Процесс обучения сети состоит из нескольких этапов. Подается входной обучающий вектор из массива данных, производится прямой проход по сети для вычисления текущего значения выхода сети. Сравниваются значения выхода сети и значения выхода тестового вектора, производиться обратный проход по сети для корректировки весовых значений связей сети для данного тестового вектора. Повторяется процесс для каждого вектора из тестового массива. Один полный цикл обучения сети включает в себя полный перебор всех тестовых векторов. На рис 4.4 (1) изображена зависимость времени выполнения одного цикла обучения сети от количества тестовых векторов в массиве данных. Расчет производился на машине класса IBM PC с процессором Pentium-120МГц. На рис 4.5 (1) показана зависимость времени сходимости тестового массива до ~ 2% ошибки.
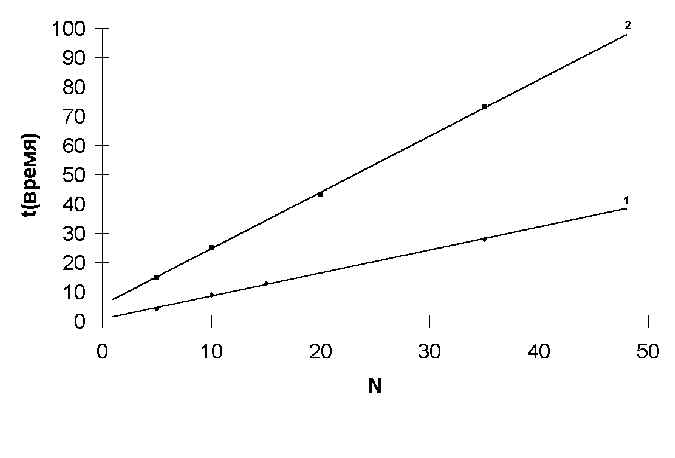 Аппроксимация
временной зависимости одного цикла
обучения от количества обучающих
векторов Рис 4.
Аппроксимация
временной зависимости одного цикла
обучения от количества обучающих
векторов Рис 4.

Аппроксимация временной зависимости времени обучения сети от количества обучающих векторов Рис 4.5
На время сходимости данного алгоритма так - же сильное влияние имеет коэффициент скорости обучения (h) который обычно имеет значения в пределах от 0,1 до 1. Коэффициент определяет нам размер шага обучения, если взять слишком малое значение то сходимость будет очень медленная, если размер шаг будет слишком велик, то может возникнуть неустойчивость сети или паралич сети. Величину коэффициента, поэтому обычно выбирают либо, исходя из опыта, либо производят уменьшение значения коэффициента пропорционально количеству циклов обучения.
При увеличении количества входных тестовых векторов уже не достигается заданная точность. Для достижения более точных значений можно увеличить длительность обучения, однако это приведет к дополнительным временным затратам.
Оптимизированный алгоритм сети обратного распространения. Отличие данного алгоритма от обычного алгоритма сети обратного распространения в наличии оптимизированной структуры связей сети и присутствии функций принадлежностей, заданных экспертами, для входных и выходных значений. Для данной сети экспертами уже были выделены правила работы по этому в задачу ее обучения входит только точная оптимизация функций принадлежности.
Работа оптимизированного алгоритма аналогична работе обычного алгоритма. Подается входной обучающий вектор из массива данных, при прямом проходе сеть высчитывает текущие значение выхода, при обратном проходе производится коррекция центров и ширин функций принадлежности. Один полный цикл обучения включает в себя полный перебор всех обучающих векторов массива данных.
На рис 4.4 (2) показана зависимость времени выполнения одного цикла обучения от количества входных обучающих векторов. На рис. 4.5 (2) показана зависимость времени сходимости тестового массива. На рис 4.6-4.11. показано смещение исходных входных и выходных функций принадлежности после обучения

Рис 4.6
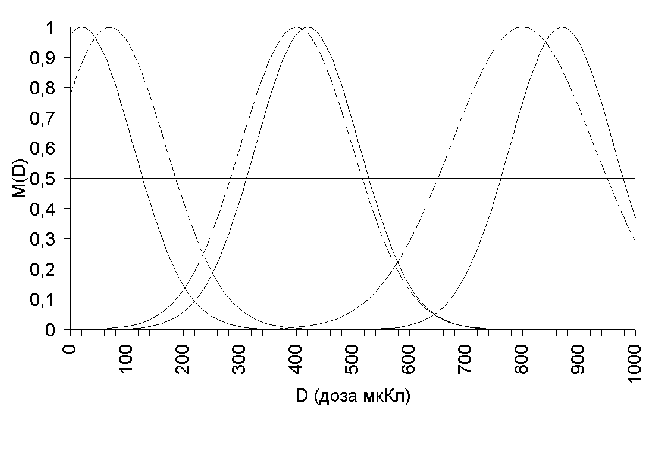
Рис 4.7
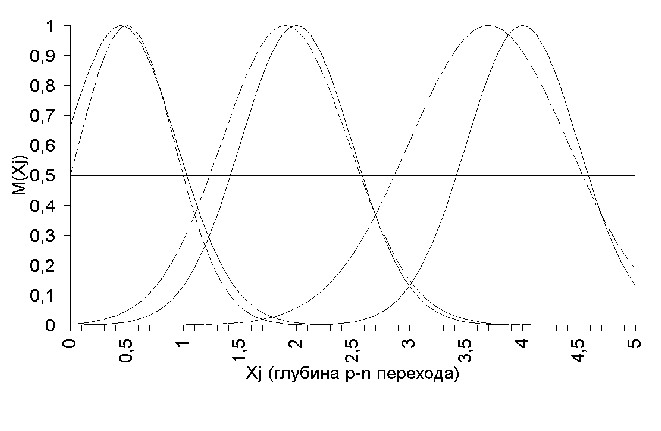
Рис 4.8
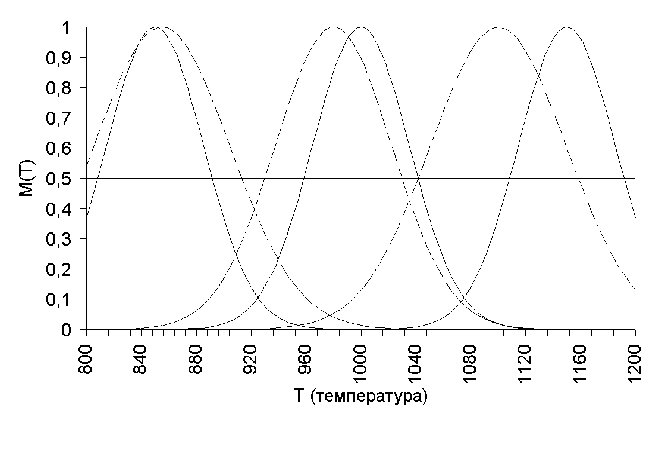
Рис 4.9
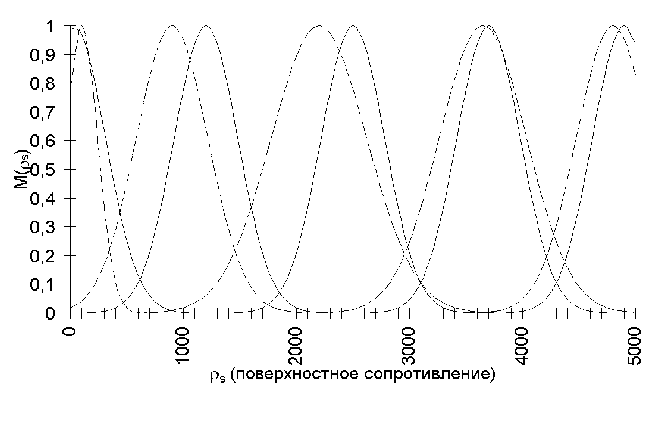
Рис 4.10
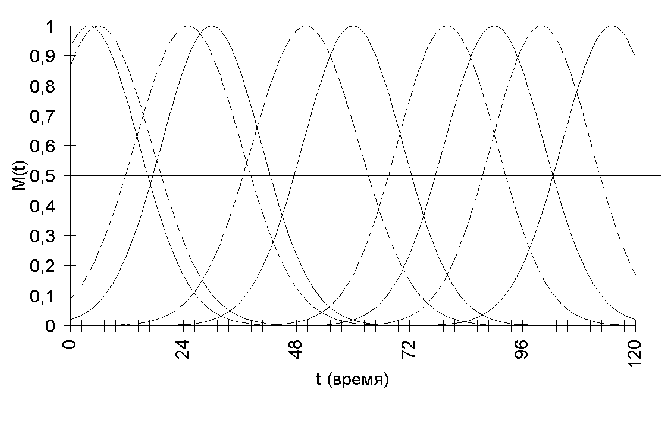
Рис 4.11
Как и в обычном алгоритме сети обратного распространения, на сходимость сети влияет коэффициент обучения сети. Благодаря оптимизированной структуре сети несмотря на большее, чем у обычного алгоритма, время выполнения одного цикла обучения скорость сходимости данной сети намного выше т.к. сеть практически не затрачивает время на определение правил. Большая часть времени при обучении затрачивается на оптимизацию функций принадлежности на данный массив векторов. Чем выше точность экспертной оценки функций принадлежности, тем выше скорость сходимости сети. Хотя время обучения занимает часы работа уже обученной системы происходит за доли секунд. В таблице 4.2 показаны результаты работы обученного нейронечеткого контроллера.
Таблица 4.2
Результаты работы нейронечеткого контроллера
Исходная структура: КЭФ - 4,5
|
Входные параметры |
Выходные параметры | |||||||
|
№ |
Энергия keV |
Доза см-2 |
Примесь |
rS Ом/кв |
xj Ом/кв |
Время, мин |
Тем-ра 0С |
Среда |
|
1 |
20 |
1015 |
Бор |
152 |
0.5010 |
17.3 |
899.8 |
О2 |
|
2 |
20 |
2*1015 |
Бор |
83 |
0.5200 |
37.8 |
898.7 |
О2 |
|
3 |
5 |
1015 |
Бор |
145 |
0.3800 |
6.4 |
995.5 |
О2 |
|
4 |
5 |
5*1015 |
Бор |
340 |
0.4975 |
34 |
798.9 |
О2 |
|
5 |
10 |
1015 |
Бор |
165 |
0.4200 |
17.5 |
947.6 |
О2 |
|
6 |
10 |
8*1014 |
Бор |
200 |
0.400 |
26.3 |
934.7 |
О2 |
|
7 |
35 |
4*1015 |
Бор |
110 |
0.8100 |
36.4 |
812.2 |
О2 |
|
8 |
35 |
1015 |
Бор |
130 |
0.6800 |
34.5 |
922.4 |
О2 |
|
9 |
10 |
1015 |
Бор |
240 |
0.3900 |
26.6 |
844.6 |
N2 |
|
10 |
35 |
2*1015 |
Бор |
65 |
0.7400 |
5.4 |
973.4 |
N2 |
В результате обучения с достаточной степенью точности проведена настройка алгоритмов и получены выходные значения соответствующие тестовым значениям. Обучение проводилось на простых примерах являющихся в большой степени упрощенными по сравнению с реальными задачами, что связано с вычислительными трудностями решения подобного класса задач на персональных компьютерах. Однако моделирование показало принципиальную работоспособность и перспективность рассмотренных алгоритмов для задач автоматизации производства. Хотя реальные задачи требуют более разнообразного представления элементов и их взаимодействия, чем в рассмотренных сетях, однако в этом случае представленные алгоритмы можно использовать как базовые.
