все билеты по сопромату

13.Линейные и угловые деформации. Тензор деформации. Геометрич. истолкование компонент ТД. Рис.: оси xyz, на них кубик dV = dxdydz. Рис.2: оси только х и у, на них квадратик dydx (начальное сост.). На расстоянии u по x и U по y тот же кубик, но уже ромбик. Его стороны dx + ( u/ x)dx; dy + ( U/ y)dy, отклонение верт. стороны на угол , горизонт. на , левый нижн. угол ( /2) - ху, отклонение вертикальной стороны от вертикали ( U/ y)dy, горизонт. стороны от горизонтали – ( u/ x)dx. Учитывая гипотез. о малости деформаций, получаем td ,tg .Тогда x=(dx +

( u/ x)dx – dx)/dx = u/ x. ху + = u/ y + U/ x. Получаем соотн. Коши: x = u/ x. y = u/ y. z

= u/ w. ху = u/ y + U/ x. ху = u/ z + w/ x. ху = U/ z + w/ y. ТН модно представить в виде

yx, yy, yz; zx, zy, zz). ТД обладает теми же св-вами что и ТН и полностью определяет деформир.

сост. тела. Все ф-лы одинаковы. Относит. изменение объема: = V/V = ((dx + xdx)(dy + ydy)(dz +

zdz) – dxdydz)/dxdydz = (dxdydz + ( x + y + z)dxdydz + x y zdxdydz + + dxdydz)/dxdydz = x + y + z

(т. к. ~ 10-3 … 10-5). Итак, = V/V = x + y + z = I1 - первый инвариант ТД. Если I1 = = 0, это означ., что деформ. не сопровожд. изменением объема. ТД может быть представлен в виде: = Sph + Dev . Ур-ия неразрывности деформации. Соотн. Коши связывают 6 ф-ий коорд. с 3-мя ф-иями

перемещ. (u, U, w). Исключим из соотн. Коши u, U, w: x = u/ x. y = u/ y. z = u/ w.

( 2/ y2)( x) + ( 2/ x2)( y) = ( 2/ y2)( u/ x) + ( 2/ x2)( u/ y) = 3u/ x y2 + 3U/ y x2 = ( 2/ x y)( u/ y +

U/ x). Получ. тождества Сенвенана: ( 2/ y2)( x) + ( 2/ x2)( y) = ( 2/ x y) ху; ( 2/ z2)( y) + ( 2/ y2)( z) = ( 2/ y z) yz; ( 2/ z2)( x) + ( 2/ x2)( z) = ( 2/ x z) хz.

СМ ФОТО

14. Закон Гука при растяж. / сжатии. Закон Гука при сдвиге. Обобщенный закон Гука. Связь межу объемным модулем, модулем Юнга и коэфф. Пуассона. Упругость – св-во тел восстанавливать первонач. размеры после снятия внеш. нагрузок. Правельнее говорить не о хрупких или пластичных матер. а о хрупком и пластичном состояниях в-ва. Количественно, упругость выраж. в том, что компоненты тензора напряж. явл. однозначными ф-ями тензора деформации, которые универсальны для данного материала и не зависят от порядка следования деформации, т. е. jk = Ф( jk). Объемный закон Гука. Закон Гука при сдвиге. Материалы по разному ведут себя по отношению к объемной деформации или к сдвигу. Sph = 3K ph . Dev = 2GDev . Или = K , = G . К – объемный модуль упругости, G – модуль сдвига. (справедливы для изотропн. мат.). Закон Гука при растяж. / сжатии. Рис. стержень, растяг. силой Р, первоначально / после деформ.: длина l / l + l; диаметр b / b + b. Вычислим отн. лин. деформации: = l/l; ' = b/b. = '/ - коэфф.

Пуассона. Закон Гука: = Е , Е – модульупругости (модуль Юнга). Е, достаточно легко вычисл. из опыта на растяж/сжатие. х = x( x) + x( y) + x( z) = x/E + (- y/E) + (- z/E) = (1/E)( x - ( y +

z)). Итак, ОЗГ: х = (1/E)( x - ( y + z)), y = (1/E)( y - ( x + z)), z = (1/E)( z - ( x + y)). = G -

для сдвига, xy = xy/G; xz = xz/G; yz = yz/G. это тоже ОЗГ. Для изотроп. материала эти 3 константы Е, , G не явл. независ: G = E/(2(1 + )). Связь межу объемным модулем, модулем Юнга и коэфф. Пуассона. Введем среднее или гидростатич. давление: = (1/3)( x + y + z). Знаем, что = x

Вообще: 0 (из термодинамич. сообр, иначе вечн. двигат.) К ,0 ½. Для каучука ½, для пробкового дерева 0.

СМ ФОТО

15. Испытания на растяж. Основные механич. хар-ки конструкционных материалов. Опыт на растяж – это почти единств. возм. осущ. однород. напряж. сост. Образец – на нем риски, Ø 10мм. График.: оси и , график растяжения.Основные точки: пц – предел пропорциональности, т –

площадка текучести, в – предел прочности - макс. , разруш. Линии Чернова-Люберса, есть следы выхода дислокаций на пов-ть. 2-е хар-ки: относительное сужение после разрыва: = ((lk –

l0)/l0)*100%. Относит. сужение после разрыва: = ((Fk – F0)/F0)*100%. Все условно, т. к. отнесено к F0, d0. Эффект Баушингера. Два графика. после разгружения переходим в точку О'. Повторное нагруж. происх. по линии О'К. Теоретич. прочность. Если считать структуру материала идеальной, то в этом случае прочность его была-бы на 2…3 порядка выше. Такое расхожд. объясняется наличием дислокаций – деффектов КР.Их плотность может достигать 107…108 см/см3 [длина дислокац./объем]. Различные факторы, оказ. влияние на прочность: вид материала, форма и размер тела, протяженность нагружения (деформирования), число циклов нагрузки, t , скорость нагрузки, степень агрессивности окруж. среды, внешнее излучение и др. некотор. переходная зона изменения указ. параметров, котор. разделяет область пластич. разруш. от хрупкого. Эксплуатац. констр. в области хрупкого разр. недопустима. Факторы, вызыв. охрупчивание: содерж. С в мат, близость напряж. сост. к всестороннему равномерн. нагруж., термообработка, увеличение габаритов конструкции (масштабный фактор), концентрац. напряжений, t окруж. среды,радиоакт. Излуч.

СМ ФОТО

17. Общие вопросы надежности конструкций и элементов энергофизического оборудования. Прочность, жесткость, устойчивость элементов конструкций. Допускаемые напряжения и коэффициент запаса прочности. Механика материалов и конструкций – наука о расчёте машин,

конструкций и их элементов на прочность, жесткость и устойчивость. Надежность – комплексное свойство технического объекта (прибора, устройства, машины, системы), заключающееся в его способности выполнять заданные функции, сохраняя свои основные характеристики (при опред. условиях эксплуатации) в установленных пределах. Понятие надёжности включает безотказность, долговечность,

ремонтопригодность, сохраняемость, живучесть, и т.д. Безотказность – свойство изделия сохранять работоспособность в течение некоторого времени или вплоть до выполнения определенного объема работы без вынужденных перерывов в заданных условиях эксплуатации.Прочность – способность конструкции сопротивляться действию внешних нагрузок и др. воздействий (температура, смещений опор, …) не разрушаясь. Жесткость: если в процессе нагружения изменения размеров и форм незначительны и не приводят к нарушению эксплуатационных свойств, то говорят, что конструкция обладает необходимой жесткостью. Устойчивость: если усилия приводят к малым и исчезающим после снятия воздействия отклонениям, то такое состояние равновесия называется устойчивым. Расчёт этих трёх параметров служит обеспечением механической надежности. В общем случае для пластических материалов условие прочности

пред

Необходимость введения нормативного коэфф. запаса обусловлена следующими факторами:1)неполная достоверность сведений о величине и характере внешних нагрузок.2)наличие разброса механических свойств материала.3)несовершенство расчётной схемы.4)несовершенство изготовления, монтажа, условий работы.

Кроме того, учитывает назначение, степень ответственности, срок эксплуатации, и т.д.

18. Принцип Сен-Венана. Понятие о концентрации напряжений. На достаточном расстоянии от места приложения системы сил статически эквивалентных нулю напряжения деформации в упругом теле,

распределена по достаточно по сравнению с характер. размерами тела Фундамент. следствие из этого принципа:если силы приложены на малом по сравнению с характер. размерами тела участке, то напряж. деформир. сост. на достаточном удалении от места приложения системы сил полностью определяется статическим эквивалентом данной сист. сил. Поня-тие о концентрац. напряжений.Имеется широкий класс задач,к кот. принцип Сен–Венана неприменим. Это связано в основном с наличием концентраторов напряжений.Концентрация напряжений– локальное отклонение однородных полей напряжений вблизи окрестности

резких изменений формы и размеров тела, а также в окрестности площади нагружения.

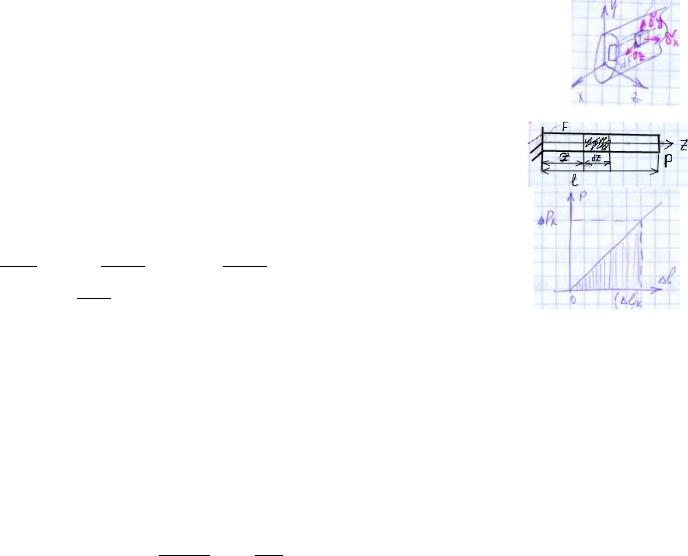
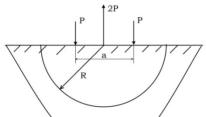
19. I)Конструкции, работающие на растяжение (сжатие). Осевая деформация прямолинейного стержня.II)Работа внешних сил и потенциальная энергия упругой деформации

или растяжения(сжатия).I)Рассмотрим осевую деформацию стержней с

криволинейной осью, такая деф-ция возможна, когда внешние нагрузки сводятся к главному вектору.̅̅̅̅̅̅̅̅ ̅ При этом линия действия главного вектора

совпадает с направлением продольной оси стержня, центральное напряжение.При изучении осевой деф-ции прямого стержня есть гипотезы:1)гипотеза плоских сеченийсечения плоские по деф-ции остаются плоскими и паралел. Друг

силы прикла-дываются квазистатически, перемещение точек тела малы, потери энергии на трение, перемагнич. малы. A=0.5P* dU=dA=0.5Nz( )

( ) ( ).U=0.5∫ ( )-общий случай. В случае если Nz

и EF -const U=0.5 . При вычислении потенц. Энергии упругой деф-ции принцип суперпозиции неприменим и нелинейно относится Nz

Интеграл Максвелла-Мора для случая растяжения(сжатия). Определения взаимных и температурных перемещений. Будем исходить из того, что вся работа совершенная внеш. силами переходит в энергию упругой деф-ции. Искомое переме-щение войдет в ур-ие А=U лишь в том случае, если в направлении этого перемещ. В сист. будет приложена сила, кот. совершает на этом перемещ. Т.к в общем случае такая сила может и не быть.Приложим в точку к случайную силу

перемещение сечений, при этом суммирование проводится в участке k1, только здесь Nk1k2 отличается от 0. =∑ ( ̅̅̅̅). = ∑ ̅̅̅̅ –

температ.перемещ. Слогаемые в этой форму. будет положит. если характер деф-ции от температурного поля и от единичной нагрузки одинаково.

20-21 Статически опред. и статич. неопред. системы. Каноническое ур-е метода сил. Сист.,

реакц. внеш. и внутр. связей в котор. можно найти, используя лишь ур-ия статики, наз. статически определимыми. Канонич. метод сил. Для опред. усилий в статич. неопред. конструкциях. Алгоритм: 1. составляем основную систему в каторой искомые усилия заменяем силами Х1, Х2, … Хn. 2. определяем все усилия Nj1¯ под действием только силы Х1, затем Nj2¯ для Х2 и т. д… причем другие Х и внеш. нагрузка Р приравн. к 0. (j – номер стержня). 3. определяем все усилия Njр в стержнях под действием внешней нагрузки Р, без учета "лишних" стержней. 4. определяем коэфф. hk =

j=1m(Njh¯Njk¯lj/EFj). kp = j=1m(Njk¯Njplj/EFj). j = 1, 2, …, m – номер стержня. 5. составляем и

решаем систему n ур-ий: 11Х1 + 12Х2 + … + 1nХn + 1р = 0; …; n1Х1 + n2Х2 + … + nnХn + nр = 0.

Находим Х1, Х2, … Хn. 6. наконец, находим истинные усилия в стержнях по ф-ле: Nj = Nj1¯Х1 + … + Njn¯Хn + Njp. Определение монтажных усилий.Пусть один стержень на короче, чем надо. Приложим в этом стержне стягивающее точки усилие Х1. Уравнение будет иметь вид: 11Х1 = . Отсюда находим Х1 и все остальное.

СМ ФОТО

22. Расчет элементов конструкций, работающих на изгиб. Классификац. видов изгиба. Дифф. зависимости между внутр. силовыми факторами при изгибе. Изгиб – это такой вид деформации,

когда в поперечном сечении стержня возникает изгибающий момент. Геометрич. хар-ки поперечн.