все билеты по сопромату

8. Необходимые условия равновесия абсолютно твёрдого тела.

(они же и достат.). n = 6. Эти условия F = 0, G = 0. Абс. тв. тело нах. в равн. тогда и только тогда, когда главн. вектор и главн. момент всех внешн. активн. и реакт. сил = 0. Т. равновес. АТТ не наруш, если действ. на него силы перенести по линии их действия (скользящ. векторы), но это утв. может быть ошибочно при кол-ве тел в сист. 1.Частные случаи: сист. сход. сил (в одну точку): G = 0 (всегда), условие: F = 0. Парралельн. сист. сил. Fj || OZ. Тогда условия: Fx = 0, Gx = 0, Gy = 0.

Плоская сист. сил: Fj OХY. Тогда условия Fy = 0, Fz = 0, Gx = 0. Модификац.: плоская сист. сил, сход. в 1-ой точке: условия: Fy = 0, Fz = 0. плоская || сист. сил: условия: Fy = 0, Gx = 0. Система из N

АТТ: n = 6N – s в R3, и 3N – s в R2. Классификац. сист. АТТ. Системы с n 1 наз. геометрич. изменяемыми или механизмами. Сист. с n = 0 наз. конструкциями или структурами. Сист., реакц. внеш. и внутр. связей в котор. можно найти, используя лишь ур-ия статики, наз. статически определимыми. Обобщенная система коорд. отлич. от ДСК тем, что ДК явл. независ, а ОК связаны с учетом связей (???). ОК не обяз. иметь четкий геометрич. смысл.

9. Понятие о виртуальных перемещениях. Формулировка принципа виртуальных перемещений. Принцип виртуальных перемещений для систем с идеальными связями.

Вирт. или возможными перемещ. наз. любая совокупность малых перемещ. точек… При этом не треб. удовл. ур-ям движ. rj ~ = rj + rj . fk(r1 , r2 , …, rN ; t) = 0, k = 1, 2, …, s. (1), fk(r1 ~, r2 ~, …, rN ~; t) = 0, k = 1, 2, …, s. (2). Движ. rj отлич. от действ. малых движ. drj , котор. удовл. ур-ию и (1), и (2). rj - только (2). Принцип вирт. перемещ.: будем рассм. сист. со стационарн. связями, а

также предполагаем, что активн. силы явно от времени не зависят. j=1N(Fj + Rj ) rj = 0, j = 1, 2, …, N (3). Равнство (3) выражает ПВП. Это рав-во заменяет всю геометтрич. статику. Известоно, что

F dr = d'A (d'A – действит. элементарная работа (не явл. полным дифф.), по аналогии F r = 'A

– вирт. работа силы F на вирт. перемещ. r . Сист. с двухсторонними связями нах. в равновес. тогда и только тогда, когда вирт. работ всех активн. и реакт. сил на любых вирт перемещ. = 0. ПВП для сист. с идеальн. связями. Связь наз. идеальн., если работа реакции на любых ВП = 0. Rj rj =

0. j=1NFj rj = 0, j = 1, 2, …, N. (4). Важным св-вом сил реакции связей явл. то, что их полная работа при малом отклонении системы от полож. равн. =0. Применение ПВП к АТТ. Рассм. абс. тв.

свободное тело, на котор. действ. F1 , F2 , …, FN . Если сист. нах. в равн., то сист. удовл. ур-ию

j=1NFj rj = 0, j = 1, 2, …, N. Т. Шаля: Всякое перемещ. свободного АТТ из одного полож в другое может быть получено посредством поступательного и вращат. движений. rj = r0 + [ x rj ],

(5). rj - радиус-вектор j – ой точки, r0 - вектор поступат. перемещ., - вектор вращения отн.

какого либо полюса. Подставим (5) в (4). j=1N[rj x Fj ] = 0 G = 0. Отсюда след, что взятые в . слагаемые должны обращ. в 0, т. к. r0 и явл. независ. Замеч.: ПВП дает необх. и достат. усл. равновес. сил в каждой точке матер. сист. и в то же время необх. но недостат. усл. равн. для всей сист. целом. Для АТТ эти усл. будут и достат.

10. Принцип Даламбера для сист. матер. точек. Общее ур-е динамики Даламбера-Эйлера.

Распространим ПВП на случ. движения сист. Ур-ия динамики мех. сист. формально сосвадают с уравн. равновес. этой сист., если к действит. внеш. силам, внутр. силам и реакц. связей добавить фиктивные (Даламберовы) силы инерции. Fj = 0, j = 1, 2, …, N, Ij = - mj(d2r/dt2). Движ. сист. происх. так, что в любой момент t работ всех внеш. и внутр. сил, реакц. связей и даламберовых сил на любых виртуальн. перем. = 0. Итак, самое Общее ур-е динамики Даламбера-Эйлера: j=1N(Fj + Fj + Rj + + Ij ) rj = 0, j = 1, 2, …, N. Н. Е. Жуковский: "Если в некотор. момент. t остановить систему и вместе с тем приложить к ее точкам силы инерции не изменяя активные силы, то сист. будет находиться в равновесии и реакции связей останутся такими, какими они были во время движения".

11.Общие предположения о свойствах материалов. Внешние и внутренние силы. Метод сечений.Нас будет интересовать не отдельные частицы, поведение материала как целого. Реальное тело(вещ-во) заменяем некоторым идеальным (моделью). В дальнейшем – модель сплошной среды.

Применяемые гипотезы: 1)о сплошности 2)об однородности 3)об изотропности 4)о жесткости 5)о линейности Внешние силы. Классификация Наиболее существенные признаки:1)-место расположения точек приложения сил

2)по характеру изменения сил в процессе их приложения.

Внутренние силы. Метод сечений В общей механике была введена аксиома связи. В механике деформирующегося тела введем понятие внутренних связей, т.е. связей, обеспечивающих целостность тела.

Прием, позволяющий перенести внутренние силы в разряд внешних, называется методом сечений. Выберем некоторый центр

приведения(полюс). Обычно выбирается центр тяжести поперечного сечения. Эти силы можно привести к главному вектору и моменту. ̅=0; ̅=0 ∑x=0;∑y=0;∑z=0 momx=0;momy=0;momz=0

12.Тензор напряжений. Симметрия тензора напряжений. Связь между тензором напряжений и вектором напряжений по произвольной площадке, проведенной через

данную точку.Нормальные и касательные напряжения на взаимно ортогональных площадках.Казалось бы, что для полной характеристики напряженного состояния ̅1= ̅n1; ̅2= ̅n2; ̅k= ̅nk

Представим вектор ̅x в виде разложения:

̅x=σxx +̅σxy +̅σzx ̅ ̅y=σxy +̅σyy +̅σzy ̅ =>

̅z=σxz +̅σyz +̅σzz ̅

Эта матрица соответствует некоторой тензорной величине и называется тензором в данной точке.σxx;σyy;σzz – нормальные

напряжения. Остальные - касательные напряжения, они равны. Первый индекс – ось действия, второй – направление нормали к площадке, по кот. действуют эти напряжения. Четкий механический смысл приведенное правило имеет только для растяжения/ сжатия. Компоненты тензора напр.

На площадке с отрицательной внешней нормалью считаются положительными, если они направлены в сторону,

противоположную соотв. оси. Симметрия тензора напряжения

(Закон парности).Тензор напряжения является симметричным: σjk = σkj. Для доказательства закона парности необходимо составить

уравнения равновесия статики для элемента с действующими на него напряжениями на площадках с положит. и отриц. нормалями. F=σS.Связь: Через произвольную точку сплошной среды можно провести множество площадок, по которым действуют различные напряжения Pj. Задание тензора напряжений в данной точке позволяет вычислить вектор напряжения Pj , действующий по любой площадке с нормалью ̅j , проходящей через данную точку. Если задан ̃, то можно определить напряженное состояние точки. Составляя уравнения статики для выделенного,

состояние в точке полностью определенно, если заданы нормальные и касательные напряжения (тензор) по трем взаимно перпенд. площадкам, проведенным через эту точку.Нормальные напряжения, действующие на каждую площадку.Вектор ̅nn нормального напряжения, действующего по наклонной площадке определим как сумму проекций векторов p1,p2 и p3 на направление нормали ̅.pnn=p1n1+p2n2+p3n3 подставим в эту формулу формулы Коши и учтем, что σjk=σkj тогда: ̅nn=σ11n12+σ22n22+σ33n33+2σ12n1n2+2σ13n1n3+2σ23n2n3

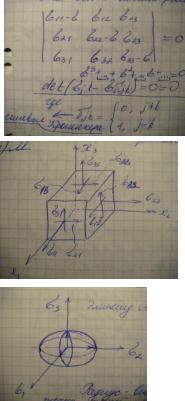
Гл напряжение и главные площадки.Для определения макс и мин значения напряжения pnn применим метод неопределенных множителей Лагранжа. Задача отыскания относительного экстремума.n12+n22+n32=1 , используя необходимое условие экстремума( равенство нулю частных производных) получаем систему

однородных уравнений:(σ11-σ)n1+σ12n2+σ13n3=0 σ21n1+(σ22-σ)n2+σ23n3=0 σ31n3+σ32n2+(σ33-σ)n3=0 эта сист. имеет решение, ежели определитель равен 0.

Получаем кубическое относительно σ уравнение, которое подчиняется след.правилу присвоения индексов: σ1σ2σ3 Площадки, по которым действуют

эти напряжения, назыв. главными. На них касательные напряжения = 0. Механ. истолкование главных напряжений.В каждой точке сплошной среды существуют 3 взаимно перпенд. площадки, по которым действуют только нормальные напряж.. Напряж. состояние в окрестности любой точ. можно представить как растяжения в 3 взаимно перпенд. направлениях, совпадающих с направлен. нормалей к главным площадкам.Элипсоид Ламе Радиус-вектор произвольной точ. такой пов-сти представл.полное напряжение на одной из площадок, положение кот. определ. Велич. М1,М2,М3. При этом одно из гл. напряж. явл. макс, другое мин. Инварианты

тензора. Разложение тензора . на сфер. тензор и девиатор. Гл. напряж., как и все напряж. состояния в данной точ. зависят от нагрузок и не зависят от выбора корд. осей =>и при других исходных напряжениях получаем одно и тоже кубическое уравнение => коэф-ты и свободные члены ур-ия инвариантны к преобразованию координат и называются инвариантами тензора напряжений в этой точке.I1=σ11+σ22+σ33 I’1=σ1+σ2+σ3

СМ ФОТО