6.6. Примеры машин Тьюринга

Представлять машину Тьюринга удобно так же, как и конечный автомат, с помощью графа переходов. В таком графе внутренним состояниям соответствуют вершины, а ребра, определяющие переход из одной вершины в другую, помечаются входным символом, выходным символом и направлением движения головки (рис. 6.5).

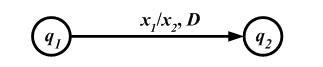
Рис. 6.5

Перед началом работы на рабочую ленту МТ наносится исходное слово и задаются начальные условия, т.е. указывается первая обозреваемая ячейка и начальное состояние. После пуска машины процесс преобразования информации происходит автоматически.

Пример 1. Построим МТ, распознающую язык {аⁿсⁿ}. Пусть начальная конфигурация этой МТ (состояние q) соответствует цепочке символов <ааассс>, а головка расположена против крайнего правого символа входной цепочки. Граф переходов такой МТ представлен на рис. 6.6.

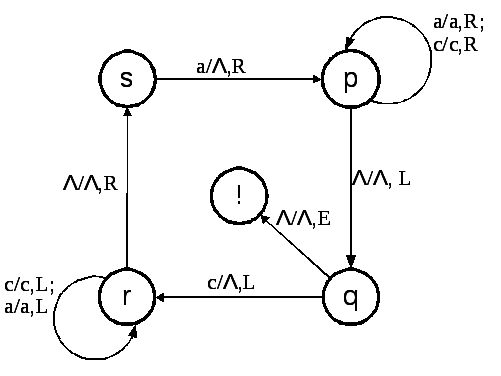
Рис. 6.6

В соответствии с графом, находясь в начальном состоянии q, головка машины считывает крайний правый символ «с», заменяет его на пустой символ Λ и сдвигается влево на одну ячейку (с/Λ,L). При этом машина переходит в следующее состояние r, в котором производится считывание символов без их изменения (с/с,L; а/а,L). Как только головка МТ вышла за пределы символьной цепочки и считала пустой символ Λ (Λ/Λ,R), головка машины начинает перемещаться вправо и машина переходит в состояние s, в котором крайний левый символ «а» заменяется на «Λ» (а/Λ,R). Затем МТ переходит в следующее состояние p, в котором, передвигая головку вправо, считывает символы без их изменения (а/а,R; с/с,R) до крайнего правого символа. Далее процесс повторяется до тех пор, пока не будут считаны и заменены на «Λ»все символы заданной цепочки, и МТ выйдет в состояние «!».

Пример 2. Рассмотрим МТ, производящую сложение двух чисел. Договоримся представлять натуральные числа в единичном (унарном) коде, т. е. для всех числовых функций алфавит исходных данных Х_исх = {1} и целое число n представляется словом 1...1 = 1ⁿ, состоящим из n единиц.

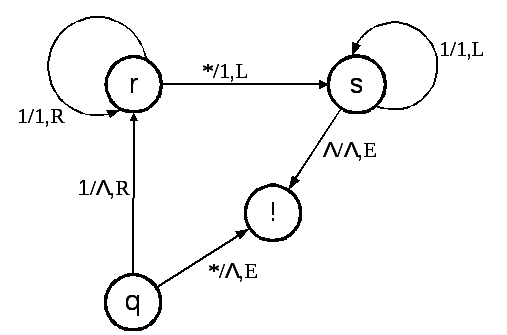
Рис. 6.7

Пусть, например, требуется сложить числа 4 и 6. Во введенном ранее представлении чисел сложить числа m и n – это значит слово 1^m * 1ⁿ переработать в слово 1^{m +n}, т.е. удалить разделитель * и сдвинуть одно из слагаемых, скажем первое, к другому.. Исходное слово на ленте запишется в виде 1111 * 111111, а начальная конфигурация определится положением головки в ячейке с крайней левой единицей и состоянием q. Это преобразование осуществляет МТ+ с четырьмя состояниями с графом переходов, изображенным на рис. 6.7.

Следуя графу переходов, на первом такте единица стирается, выдается команда сдвига вправо и перехода в состояние r (1/Λ,R). В этом состоянии производится считывание единиц без их изменения и последовательный сдвиг направо сквозь все единицы (1/1,R) до разделителя «*». Тогда вместо разделителя в ячейку вписывается единица и машина переходит в состояние s, начиная перемещать головку влево (*/1,L). Достигнув первой пустой ячейки, машина останавливается, переходя в состояние «!». В результате получим слово 1111111111, соответствующее числу 10. Переход (*/Λ,R) из состояния q в «!» предусмотрен для случая, когда а = 0 и исходное слово имеет вид «* 1ⁿ».

Пример 3. Рассмотрим МТ, которая производит определение наибольшего общего делителя двух положительных целых чисел, заданных в унарном коде. Пусть заданы два числа m = 4 и n = 6. Исходная конфигурация машины в начальном состоянии q соответствует положению головки на крайнем правом символе числа m (рис. 6.8)

Рис. 6.8

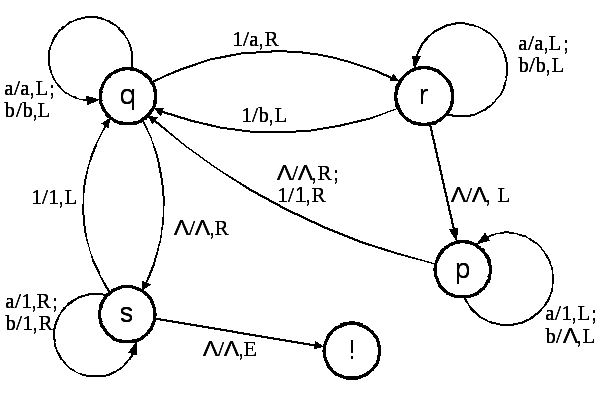
Рис. 6.9

Предоставляем читателю самостоятельно проанализировать все промежуточные конфигурации МТ в процессе отработки алгоритма по графу переходов (рис. 6.9). В процессе отработки алгоритма использованы вспомогательные промежуточные символы а и b.

Алгоритм вычисления НОД двух чисел здесь заключается в повторяющихся действиях по нахождению меньшего из двух чисел и вычитании его из большего до тех пор, пока не получатся равные числа.

Описанные машины Тьюринга являются специализированными: каждому алгоритму соответствует своя машина. Рассматривая функциональную схему как описание программы, можно прийти к понятию универсальной машины Тьюринга, которая реализует любой алгоритм, если на ее ленту, кроме исходных данных, записана соответствующая программа. Таким образом, интуитивное понятие алгоритма получает точное определение как процесс, который может быть представлен функциональной схемой и реализован машиной Тьюринга.

Контрольные задания

1. Построить машину Тьюринга, распознающую язык Дика – скобочные скелеты арифметических выражений. Примеры цепочек этого языка:

«(( ))»; «(( )) ((( ) ( )))»

2. Построить МТ, распознающую язык а^n↑2. Примеры цепочек этого языка: «а»; «аааа».

Указание: Воспользоваться соотношением: (k + 1)² = k² + 2k + 1 или тем, что квадрат натурального числа представляется как сумма последовательных нечетных чисел (2² = 1+3; 3² = 1+3+5; 4² = 1+3+5+7 и т.д.)

3. Построить МТ, распознающую язык, цепочки которого содержат одинаковые количества вхождений символов а, b, с. Пример цепочки этого языка: «b а а с b с с b а»

4. Построить МТ, увеличивающую двоичные числа на единицу.

5. Построить МТ, уменьшающую двоичные числа на единицу.

6. Построить МТ, переводящую двоичное число в унарную форму, и наоборот, из унарной формы в двоичное представление.

7. Построить МТ, переводящую число из пятеричной системы счисления в семеричную.

8. Построить МТ, переводящую число из двоичной системы счисления в восьмеричную.

9. Построить МТ, переводящую число из двоичной системы счисления в десятичную.

10. Построить МТ, подсчитывающую произведение двух заданных чисел в унарной записи.

11. Построить МТ, суммирующую 1 к числу, записанному в троичной системе счисления.

12. На ленте записано число х в троичной системе счисления. Построить МТ, записывающую на ленту число «2х», если х делится на три без остатка, и «х – 1» – в противном случае.

13. Для натуральных чисел, заданных в виде слов в алфавите 0, |, определить операцию умножения и построить МТ над алфавитом 0, |, которая для любых натуральных чисел m и n вычисляет их произведение.

14. Построить МТ над алфавитом а, b, которая:

а) к любому слову ха, b присоединяет слева (справа) заданное слово w₀;

б) распознает двойные слова в алфавите а, b;

в) удваивает произвольное слово ха, b, т.е. по этому слову вычисляет слово хх.