5.4. Эквивалентность конечных автоматов: теорема Мура

Две булевы функции F₁ и F₂ эквивалентны, если на всех возможных наборах входных переменных они принимают одинаковые значения. Поскольку число наборов у булевых функций конечно, то, перебрав их все, можно проверить, эквивалентны ли F₁ и F₂. Можно также привести F₁ и F₂ к совершенной нормальной форме и сравнить их представления.

Иная ситуация с конечными автоматами. Два конечных автомата эквивалентны, если реализуемые ими отображения вход-выход эквивалентны. Конечный автомат реализует отображение бесконечного множества входных последовательностей сигналов в бесконечное множество выходных последовательностей сигналов. Поэтому автоматные отображения нельзя сравнить простым перечислением их значений на всех возможных аргументах.

Конечные автоматы А = {X_А, Y_А, Q_А, δ_А, λ_А} и В = {X_В, Y_В, Q_В, δ_В, λ_В} называются эквивалентными, если выполняются два условия:

а) их входные алфавиты совпадают: X_А = X_В = X;

б) реализуемые ими автоматные отображения совпадают:

(χХ^*) λ_А^*(q_А, χ) = λ_В^*(q_В, χ).

Эквивалентность автоматов означает, что любое автоматное отображение, реализуемое одним из них, может быть реализовано другим; иначе говоря, их возможности по реализации преобразования входной информации в выходную совпадают. Определить эквивалентность двух автоматов перебором их реакций на всех входных словах достаточно сложно, так как входных слов бесконечно много. Однако существует достаточно простой метод решения этой проблемы, основанный на понятии прямого произведения автоматов.

Прямым произведением конечных автоматов А = {X, Y_А, Q_А, δ_А, λ_А} и В = {X, Y_В, Q_В, δ_В, λ_В} с одинаковым входным алфавитом Х называется автомат А×В ={X, Y_А×Y_В, Q_А×Q_В, δ_А×В, λ_А×В}, где:

а) (q_А Q_А) (q_В Q_В) (xХ) δ_А×В ((q_А, q_В) x ) = (δ_А(q_А, x)_, δ_В(q_В, x));

б) (q_А Q_А) (q_В Q_В) (xХ) λ_А×В ((q_А, q_В) x ) = (λ_А(q_А, x)_, λ_В(q_В, x)).

Иначе говоря, конечный автомат, являющийся прямым произведением двух конечных автоматов, в качестве своих состояний имеет пары состояний исходных автоматов, выходной алфавит – множество пар выходных символов автоматов множителей, а функции выходов и переходов определены покомпонентно. Таким образом, это просто два стоящих рядом невзаимодействующих конечных автомата, синхронно работающих на одном общем входе (рис. 5.7). Прямое произведение автоматов называется также синхронной композицией.Рис. 5.7

Теорема 5.1. (Теорема Мура) Два конечных автомата А = {X, Y_А, Q_А, δ_А, λ_А} и В = {X, Y_В, Q_В, δ_В, λ_В} с одинаковым входным алфавитом Х являются эквивалентными тогда и только тогда, когда для любого достижимого состояния (q_А, q_В) в их прямом произведении А×В справедливо (xХ) λ_А(q_А, x)= = λ_В(q_В, x).

Определение: Состояние qQ называется достижимым тогда и только тогда, когда (χХ^*) δ^* (q₀, χ ) = q (то есть по воздействием какого-либо входного слова χ автомат попадает в это состояние.

Доказательство. Пусть А и В эквивалентны, то есть по определению эквивалентности (χХ^*) λ_А^*(q_А, χ) = λ_В^*(q_В, χ).

Докажем при этом предположении:

((q_А, q_В) Q_А×Q_В) достижимо (q_А, q_В)  (xХ) λ_А(q_А, x)= λ_В(q_В, x).

В соответствии с определением, свойство достижимости состояния (q_А, q_В) эквивалентно условию (χХ^*) δ^* ((q_0А, q_0В), χ ) = (q_А, q_В). Таким образом, надо доказать, что если

(χХ^*) λ^* (q_0А, χ ) = λ^* (q_0В, χ) , то

((q_А, q_В) Q_А×Q_В)[ (ξХ^*) δ^* ((q_0А, q_0В), ξ ) = (q_А, q_В) 

 (xХ) λ_А(q_А, x)= λ_В(q_В, x)].

Предположим противное, то есть что

¬((q_А, q_В) Q_А×Q_В)[ (ξХ^*) δ^* ((q_0А, q_0В), ξ ) = (q_А, q_В) 

 (xХ) λ_А(q_А, x)= λ_В(q_В, x)], (здесь знак ¬ перед выражением определяет инверсию) и покажем, что тогда ¬(χХ^*) λ_А^*(q_0А, x) = λ_В^*(q_0В, x).

Отрицание следствия можно преобразовать в

((q_А, q_В) Q_А×Q_В)[ (ξХ^*) δ^* ((q_0А, q_0В), ξ ) =

= (q_А, q_В) & (xХ) λ_А(q_А, x) ≠ λ_В(q_В, x)].

Положим χ = ξ x. Очевидно, что

λ_А^*(q_0А, χ) = λ_А^*(q_0А, ξx = λ_А^*(q_0А ,x)^ λ_А(δ^*(q_0А, ξ) x ) = λ_А^*(q_0А, ξ)^ λ_А(q_А, x) ≠ ≠ λ_В^*(q_0В, ξ)^ λ_В(q_В, x ) = λ_В^*(q_0В, ξ)^ λ_В(δ^*(q_0В, ξ) x) = λ_В^*(q_0В, ξx) = λ_В^*(q_0В, χ).

Отсюда:

(χХ^*) λ_А^*(q_0А, χ) ≠ λ_В^*(q_0В,χ) или ¬(χХ^*) λ_А^*(q_0А, χ) = λ_В^*(q_0В, χ),

что и требовалось доказать.

Автомат Мура является частным случаем автомата Мили, однако их возможности совпадают. Между автоматами Мили и Мура имеется взаимная связь, и один их них может быть преобразован в другой.

Пример конечного автомата Мура представлен на рис. 5.8а. Здесь выход автомата определяется однозначно тем состоянием, в которое автомат переходит после приема входного сигнала. Например, в состояние 1 можно прийти по трем переходам: из состояния 0 под воздействием входного сигнала b, из состояния 2 под воздействием b, из состояния 1 также под воздействием входа b. Во всех трех случаях выходная реакция автомата одна и та же: на выходе образуется сигнал у2. Совершенно очевидно, что по любому автомату Мура легко построить эквивалентный ему автомат Мили; так для автомата Мура (рис. 5.8а) эквивалентный ему автомат Мили изображен на рис. 5.8б.

Рис. 5.8

Справедливо и обратное: для любого автомата Мили существует эквивалентный ему автомат Мура. Справедливость этого утверждения легко доказывается конструктивно. Рассмотрим автомат Мили, представленный на рис. 5.9а. Каждое состояние автомата Мили расщепляется на несколько эквивалентных состояний, с каждым из которых связывается один выходной символ. Для нашего примера это состояния р0, p1, q0, ql, r0, rl. Построение переходов эквивалентного автомата Мура ясно из рисунка 5.9б.

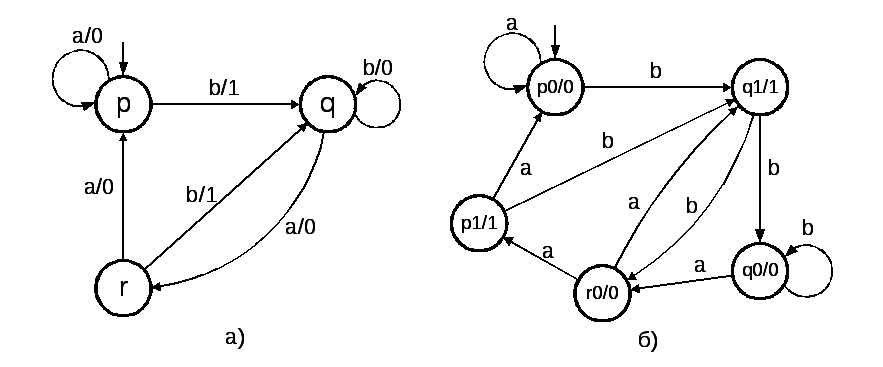Рис. 5.9

Отметим однако, что такая эквивалентность автоматов Мили и Мура не отражает их существенной разницы: выходные сигналы в автомате Мили связаны с (мгновенными) событиями переходов автомата, в то время как выходные сигналы в автомате Мура определяются при входе в его новое состояние. В примерах реальных систем, функционирование которых описывается моделью конечного автомата, обычно ясно видна разница между двумя видами выходных сигналов – импульсными сигналами, возникающими только в моменты переходов системы из одного состояния в другое, и потенциальными выходными сигналами, возникающими в момент входа в состояние и остающимися неизменными все время, пока автомат находится в текущем состоянии. В реальных системах управления часто необходимы сигналы обоих типов. Во многих применениях конечных автоматов для спецификации дискретных систем с памятью используются как выполнения функций на переходах между состояниями, так и функции входа и функции выхода, активизирующиеся соответственно в моменты входа в новое состояние и выхода из текущего состояния