4.4. Пути и контуры в графах

Существует понятие цепей в теории графов. Связка вершин и ребер образует цепь в графе. Цепь называется полной, если она связывает все вершины графа без образования петель и контуров. Цепь имеет голову и хвост. Голова цепи привязывается к какой-либо вершине, которую называют привязкой. Цепи образуют пути в графе.

Путь в неориентированном графе G – это последовательность ребер и вершин L (v_0, х₁, v₁, х₂, v₂, х₃, v₃, x _n, v _n) , где v – вершины, x – ребра. При этом вершина v₀ называется началом пути, вершина v_n – концом. Каждая прочая вершина инцидентна предыдущему ребру и последующему, поскольку конец каждого ребра совпадает с началом следующего.

Путь, состоящий из одной вершины, называется нулевым. Путь называется простым, если никакая дуга или ребро не встречается в нем дважды. Путь называется элементарным, если никакая вершина в нем не встречается дважды.

Цикл – это замкнутый путь в неорграфе. Цикл в неорграфе называется эйлеровым обходом или эйлеровым циклом, если он содержит все ребра графа в точности по одному разу. Если в графе существует эйлеров цикл, то такой граф называется эйлеровым. Необходимые и достаточные условия существования эйлерова цикла были определены великим Леонардом Эйлером и в современной терминологии формулируются в следующей теореме.

Теорема 4.1. Неориентированный граф является эйлеровым тогда и только тогда, когда он связен и все степени его вершин четны.

Необходимость. То, что в несвязном графе не может быть цикла, проходящего через все ребра, очевидно. Пусть теперь граф связен и в нем существует эйлеров цикл с началом в вершине v₁. Пройдем по этому циклу, помечая пройденные ребра. Через каждую вершину цикл может проходить несколько раз, добавляя каждый раз два помеченных ребра. При каждом проходе через вершину v₁ будет помечено нечетное число ребер (потому что при первом выходе из v₁ было помечено одно ребро), а при проходах через другие вершины – четное число ребер. Поэтому цикл может закончиться в v₁ только в том случае, когда степень v₁ четна (цикл входит по последнему непомеченному ребру, и к нечетному числу помеченных ребер добавляется единица). Во всех остальных вершинах все ребра будут помеченными, т. е. число помеченных ребер в каждой вершине будет равно ее степени, которая тем самым окажется четной.

Достаточность. Покажем, как построить эйлеров цикл в связном графе, у которого все степени вершин четны. Выберем какую-либо вершину v₁ и будем строить из нее путь в произвольном порядке, помечая уже пройденные ребра и включая в путь только те ребра, которые еще не помечены. При входе в вершину, отличную от их, помечается нечетное по счету ребро, при выходе – четное; в силу четности ее степени из нее всегда можно выйти по непомеченному ребру. Поэтому наш путь может закончиться только в v₁ (см. доказательство необходимости), образовав таким образом цикл Р₁. Если при этом все ребра графа оказались помеченными, то искомый эйлеров цикл построен. Если же это не так, то для любой вершины, имеющей инцидентные ей непомеченные ребра, их число четно. Найдем первую такую вершину на пути Р₁ (обозначим ее v₂) и будем строить из нее путь по непомеченным ребрам. По указанным выше причинам (четность всех степеней и четность числа непомеченных ребер) этот путь может закончиться только в v₂, образовав цикл Р₂. Этот цикл вставим в Р₁ в точке v₂. Получим новый цикл Р₁₂. Если и после этого остались непомеченные ребра, то строим еще один цикл Р₃ и вставляем его в Р₁₂. Этот процесс построения циклов Р_i и вставки их в уже построенный цикл Р_{(12… i – 1)} продолжаем до тех пор, пока не останется непомеченных ребер. Полученный в конечном счете цикл Р _{(12… k)} и будет эйлеровым.

Теорема 4.2. Неориентированный граф является эйлеровым тогда и только тогда, когда он связен и является объединением нескольких циклов, не пересекающихся по ребрам.

1. Пусть граф – эйлеров. Тогда эйлеров обход в нем можно построить методом, описанным в предыдущей теореме. Этот обход представляет собой объединение циклов Р₁, Р₂, … Р _k, которые не пересекаются по ребрам, поскольку каждый следующий цикл содержит только непомеченные ребра, т. е. ребра, не вошедшие в предыдущие циклы.

2. Пусть граф связен и является объединением нескольких циклов, не пересекающихся по ребрам. Тогда любое ребро графа принадлежит некоторому циклу. Если через вершину проходит только один цикл, то ее степень равна двум. Если же через вершину проходит несколько циклов, то, поскольку они не пересекаются по ребрам, каждый цикл добавляет в степень вершины ровно два ребра. Поэтому все вершины графа имеют четные степени и, следовательно, граф – эйлеров.

Гамильтонова задача: В 1859 году сэр Вильям Гамильтон, знаменитый ирландский математик, предложил детскую головоломку, в которой предлагалось совершить путешествие по 20 городам, побывав в каждом не более одного раза. Каждый город соединялся с тремя соседними так, что дорожная сеть образовывала 30 ребер додекаэдра (рис. 4.12). Например, если начать путешествие из города а, то закончить его надо в городах e, b или h, иначе нельзя будет вернуться опять в город а.

Непосредственное исчисление доказывает, что число всех таких маршрутов равно 60. Например: – (a-b-c-l-m-t-s-k-j-i-r-q-p-o-n-d-e-f-g-h). Отныне, с легкой руки сэра Вильяма, любой простой путь, который связывает все вершины графа, называется гамильтоновым. Если существует простой граф с n вершинами, и степень каждой вершины не меньше n/2, то такой граф обязательно будет гамильтоновым. Однако можно легко построить гамильтонов граф, у которого степень вершины меньше n /2.

Рис. 4.12

Пути и связность в ориентированных графах. Путь в ориентированном графе G_О – это последовательность вершин v₀,v₁,… v_n, такая, что v_i → v_i+1 для любого i, если i+1 существует.

Ряд понятий для неориентированных графов – начало, конец, длина пути, цикл, цепь, простая цепь – без изменения переносятся на орграфы. Другие понятия, и прежде всего связность и достижимость, существенно видоизменяются. Говорят, что вершина v_j достижима из вершины v_i , если суще­ствует путь с началом в v_i и концом в v_j. По определению полагаем, что любая вершина достижима из себя самой.

Контур – это ориентированный цикл в орграфе. Понятие простоты и элементарности распространяется и на циклы, и на контуры. Контур, который содержит все ребра или дуги графа, называется эйлеровым. Естественно, что контур, который проходит все вершины графа без повторения, называется гамильтоновым. Связанный орграф содержит эйлеров контур тогда и только тогда, когда для каждой вершины число входящих дуг равно числу исходящих.

Отношение достижимости между вершинами в оргра­фах несимметрично: если v_j достижима из v_i , то v_i необязательно достижима из v_j.

Полупуть в ориентированном графе – это такая последовательность ребер, когда любые два соседних ребра различны и имеют общую инцидентную им вершину.

Таким образом, в орграфах существуют различные виды связности, которые описываются следующими определениями.

1. Орграф называется сильно связным, если любые две вершины достижи-мы друг из друга (т. е. если между ними существуют пути в обе стороны).

2. Орграф называется односторонне связным, если для любой пары вершин существует путь между ними хотя бы в одну сторону.

3. Орграф называется слабо связным, если между любой парой вершин существует полупуть.

4. Орграф называется несвязным, если между некоторой парой вершин нет полупути (т. е. если он не является слабо связным).

Длиной пути называется число ребер от вершины v_i к вершине v_j. Длина может быть различной для пути между двумя вершинами.

Если рассматривать путь с минимальным числом ребер от вершины v_i к вершине v_j, то такой путь называется расстоянием r (v_i ; v_j). Если между вершинами не существует никакого пути, то r = ∞.

Диаметром d(G) графа G называется максимальное расстояние между его вершинами:

d(G) = max d(v_i; v_j).

Для любой вершины можно определить среднее отклонение от центра графа по формуле

D (v_i) = 1/m∑ r(v_i; v),

где m – число дуг в графе G, а v – пробегает все вершины графа.

Вершина, для которой D(v_i) окажется минимальной, называется центром графа. Может быть несколько вершин, являющихся центром.

Максимальное удаление r(v_i) от центра графа называется радиусом графа G и обозначается r(G ).

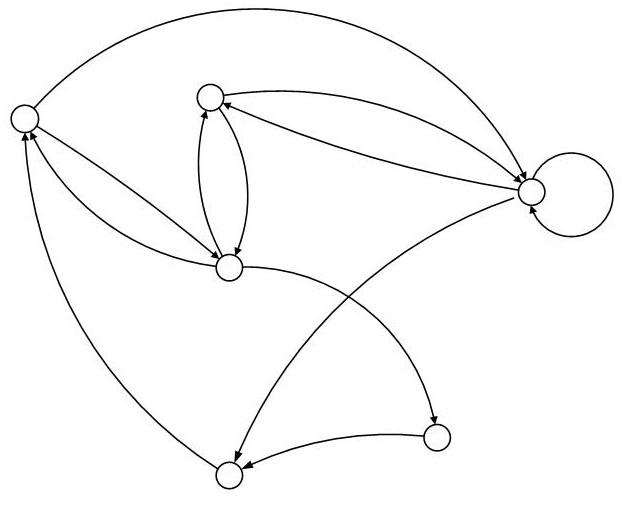
Рассмотрим орграф G₁ с количеством вершин n = 6 и числом дуг m = 12, изображенный на рис. 4.13.

Построим матрицу R=||r_ij||, которая отражает все расстояния между вершинами графа G₁. На ее основе можно рассчитать все возможные отклонения вершин от центра графа:

D₁ = 8/12; D₂ = 8/12; D₃ = 9/12; D₄ = 13/12; D₅ = 11/12; D₆ = 7/12.

Таким образом, вершина v₆ является центром графа G₁.

2 1 2 3 4 5 6

1 0 2 1 2 2 1 1

3 2 0 1 2 2 1 2

2 1 0 3 1 2 3

R(G₁) = 2 4 3 0 1 3 4

6 1 3 2 3 0 2 5

1 1 2 1 2 0 6

4

5

Рис. 4.13

Чтобы пересчитать все возможные пути длиной r, рассмотрим различные степени матрицы смежности графа G₁.

1 2 3 4 5 6 1 2 3 4 5 6

0 0 1 0 0 1 1 1 2 1 1 1 0 1

0 0 1 0 0 1 2 1 2 1 1 1 0 2

А(G₁) = 0 1 1 0 1 0 3 А²(G₁) = 1 1 2 0 1 1 3

0 0 0 0 1 0 4 1 0 0 0 0 0 4

1 0 0 0 0 0 5 0 0 1 0 0 1 5

1 1 0 1 0 0 6 0 0 2 0 1 2 6

1 2 3 4 5 6 1 2 3 4 5 6

1 1 4 0 2 3 1 6 8 18 2 9 12 1

1 1 4 0 2 3 2 6 8 18 2 9 12 2

А³(G₁) = 2 3 4 1 2 2 3 … А⁵(G₁) = 10 14 19 5 11 10 3

0 0 1 0 0 1 4 1 1 4 0 2 3 4

1 2 1 1 1 0 5 5 7 6 3 4 2 5

3 4 2 2 2 0 6 11 16 13 7 9 4 6

Матрица смежности А(G₁) дает число путей, длина которых равна одной дуге. Квадрат матрицы А²(G₁) дает число путей, длина которых равна двум. Куб матрицы А³(G₁) – число путей в три дуги и т.д.

Существует понятие означенной матрицы смежности Аⁿ(G₁), в которой вместо единиц проставляются соответствующие вершины, т.е. означенная матрица, помимо числа путей, указывает еще и вершины, через которые эти пути пролегают. Тогда на диагонали означенной матрицы будут указаны всевозможные контуры, длина которых определяется степенью матрицы. Ниже показаны означенные матрицы первой и второй степени.

1 2 3 4 5 6 1 2 3 4 5 6

0 0 13 0 0 16 1 161 132 1 1 1 0 1

162

0 0 23 0 0 26 2 261 232 1 1 1 02

262

А(G₁) = 0 32 33 0 35 0 3 А²(G₁) = 351 1 323 0 1 1 3

333

0 0 0 0 45 0 4 451 0 0 0 0 0 4

51 0 0 0 0 0 5 0 0 1 0 0 1 5

61 62 0 64 0 0 6 0 0 613 0 1 616 6

623 626

Неповторяющиеся вершины для отдельных путей укажут на элементарные пути. Поскольку граф G₁ имеет шесть вершин, то элементарных путей, длина которых равнялась бы шести дугам, вообще не может быть. Таким образом, максимальная степень означенной матрицы для определения всех гамильтоновых путей должна равняться n – 1, т.е. пяти. Если в такой матрице оставить только те пути и контуры, которые являются гамильтоновыми, то получим

1 2 3 4 5 6

162351 0 0 0 132645 0 1

0 235162 264513 235164 0 0 2

А⁵(G₁) = 326451 0 351623 0 0 0 3

0 451623 0 0 0 451326 4

0 0 0 513264 516235 0 5

0 645132 0 0 0 623516 6.

В нашем графе G₁, как показывает матрица А⁵(G₁), разных гамильтоновых путей только три: 326451, 451623 и 235164. На диагонали оставлен один и тот же простой контур 162351, который, однако, гамильтоновым не является.